
- •1. Предмет теории вероятностей
- •Классическое определение вероятности
- •Геометрическое определение вероятности
- •Теорема сложения вероятностей и ее следствия
- •Условная вероятность
- •Теорема умножения вероятностей.
- •3. Формулы полной вероятности и формула Байеса
- •Определение
- •Свойства
- •Тождества
- •Числовые характеристики дискретных случайных величин
- •Зависимые и независимые случайные величины
- •Свойства
- •Свойства коэффициента корреляции
- •11. Числовые характеристики непрерывных случайных величин
- •Свойства
- •Определение
- •Свойства распределения Пуассона
- •Равномерное распределение.
- •Центральная предельная теорема Ляпунова.
- •Исправленная выборочная дисперсия
- •Определение
Определение
Пусть
дано вероятностное
пространство
![]() ,
и на нём определена случайная
величина
X
с распределением
,
и на нём определена случайная
величина
X
с распределением
![]() .
Тогда функцией распределения случайной
величины X
называется функция
.
Тогда функцией распределения случайной
величины X
называется функция
![]() ,
задаваемая формулой:
,
задаваемая формулой:
![]() .
.
Свойства
-
FX непрерывна справа:[1]
![]()
-
FX не убывает на всей числовой прямой.
-
 .
. -
 .
.
-
Распределение случайной величины
 однозначно
определяет функцию распределения.
однозначно
определяет функцию распределения.
-
Верно и обратное: если функция F(x) удовлетворяет четырём перечисленным выше свойствам, то существует вероятностное пространство и определённая на нём случайная величина, такая что F(x) является её функцией распределения.
-
-
По определению непрерывности справа, функция FX имеет правый предел FX(x + ) в любой точке
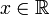 ,
и он совпадает со значением функции
FX(x)
в этой точке.
,
и он совпадает со значением функции
FX(x)
в этой точке.
-
В силу неубывания, функция FX также имеет и левый предел FX(x − ) в любой точке
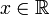 ,
который может не совпадать со значением
функции. Таким образом, функция FX
либо непрерывна в точке, либо имеет в
ней разрыв
первого рода.
,
который может не совпадать со значением
функции. Таким образом, функция FX
либо непрерывна в точке, либо имеет в
ней разрыв
первого рода.
-
Тождества
Из
свойств вероятности
следует, что
![]() ,
таких что a
< b:
,
таких что a
< b:
-
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 .
.
Числовые характеристики дискретных случайных величин
\
|
Математическое ожидание M дискретной случайной величины - это среднее значение случайной величины, равное сумме произведений всех возможных значений случайной величины на их вероятности.
|
0Свойства математического ожидания:
-
Математическое ожидание постоянной величины равно самой постоянной
 .
. -
Постоянный множитель можно выносить за знак математического ожидания
 .
. -
Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий
 .
.
-
Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых
Для описания многих практически важных свойств случайной величины необходимо знание не только ее математического ожидания, но и отклонения возможных ее значений от среднего значения.
|
Дисперсия случайной величины — мера разброса случайной величины, равная математическому ожиданию квадрата отклонения случайной величины от ее математического ожидания.
Принимая во внимание свойства математического ожидания, легко показать что
|
Казалось бы естественным рассматривать не квадрат отклонения случайной величины от ее математического ожидания, а просто отклонение. Однако математическое ожидание этого отклонения равно нулю. Это объясняется тем, что одни возможные отклонения положительны, другие отрицательны, и в результате их взаимного погашения получается ноль. Можно было бы принять за меру рассеяния математическое ожидание модуля отклонения случайной величины от ее математического ожидания, но как правило, действия связанные с абсолютными величинами, приводят к громоздким вычислениям.
0Свойства дисперсии:
-
Дисперсия постоянной равна нулю.
-
Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
-
Если x и y независимые случайные величины , то дисперсия суммы этих величин равна сумме их дисперсий.
7. Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления.
Биномиальное распределение
Пусть проводится серия из n независимых испытаний, каждое из которых заканчивается либо “успехом” либо “неуспехом”. Пусть в каждом испытании (опыте) вероятность успеха p, а вероятность неуспеха q = 1- p. С таким испытанием можно связать случайную величину x , значение которой равно числу успехов в серии из n испытаний. Эта величина принимает значения от 0 до n. Ее распределение называется биномиальным и определяется формулой Бернулли
![]() ,
0 < p
<1,
k
=
0, 1, …, n,
,
0 < p
<1,
k
=
0, 1, …, n,
![]() ,
Mx
=
np,
Dx
=
npq,
,
Mx
=
np,
Dx
=
npq,
![]() .
.
Геометрическое распределение
Со
схемой испытаний Бернулли можно связать
еще одну случайную величину x - число
испытаний до
первого
успеха.
Эта величина принимает бесконечное
множество значений от 0 до +![]() и ее распределение определяется формулой
и ее распределение определяется формулой
pk
=
P(x=
k)
= qk-1
p,
0 <p
<1,
k=1,
2, … ,
![]() ,
,
![]() ,
,
![]() .
.
Гипергеометрическое распределение
В партии из N изделий имеется M (M < N) доброкачественных и N - M дефектных изделий. Если случайным образом из всей партии выбрать контрольную партию из n изделий, то число доброкачественных изделий в контрольной партии - случайная величина, которую обозначим x. Распределение такой случайной величины называется гипергеометрическим и имеет вид:
 ,
k
=
0, 1, …, min(n,M),
,
k
=
0, 1, …, min(n,M),
 ,
,
![]() ,
,
![]() .
.
8.
одном
и том же случайном эксперименте можно
рассматривать не одну, а несколько - n
-
числовых функций, определенных на одном
и том же пространстве элементарных
событий. Совокупность таких функций
называется многомерной
случайной величиной или
случайным
вектором
и обозначается
![]() .
.
Точнее.
На вероятностном пространстве
![]() заданы
случайные величины
заданы
случайные величины
![]() ;
каждому w
;
каждому w
![]() W
эти величины ставят в соответствие
n-мерный
вектор
W
эти величины ставят в соответствие
n-мерный
вектор
![]() ,
который называется n-мерным
случайным
вектором (n-мерной
случайной величиной).
,
который называется n-мерным
случайным
вектором (n-мерной
случайной величиной).
Многомерные случайные величины. Функции распределения многомерных случайных величин.
Функцией
распределения случайного вектора
![]() или
совместным
распределением случайных величин
или
совместным
распределением случайных величин
![]() называется
функция, определенная равенством
называется
функция, определенная равенством
![]() ,
,
где
![]() .
.
По
известной многомерной функции
![]() можно
найти распределение каждой из компонент
можно
найти распределение каждой из компонент
![]() .
.
Например,
если
![]() -
двумерная случайная величина, имеющая
совместное распределение
-
двумерная случайная величина, имеющая
совместное распределение
![]() ,
то распределения компонент
,
то распределения компонент
![]() и
и
![]() вычисляются
соответственно по формулам:
вычисляются
соответственно по формулам:
![]() ,
,
![]() .
.
В дальнейшем будем рассматривать двумерные случайные векторы.
Случайный
вектор
![]() называется
непрерывным
случайным вектором,
если существует такая неотрицательная
функция
называется
непрерывным
случайным вектором,
если существует такая неотрицательная
функция
![]() ,
что для любого прямоугольника W на
плоскости
,
что для любого прямоугольника W на
плоскости
![]() вероятность
события
вероятность
события
![]() равна
равна
![]() .
.
Функция
![]() в
этом случае называется совместной
плотностью распределения.
в
этом случае называется совместной
плотностью распределения.
Легко
показать, что
![]() .
.
Если
![]() -
совместная плотность распределения
двумерного случайного вектора
-
совместная плотность распределения
двумерного случайного вектора
![]() ,
то плотности распределения его компонент
определяются равенствами:
,
то плотности распределения его компонент
определяются равенствами:
 и
и
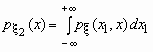 .
.
Если
![]() -
дискретный случайный вектор, то совместным
распределением случайных величин
-
дискретный случайный вектор, то совместным
распределением случайных величин
![]() и
и
![]() чаще
всего называют таблицу вида
чаще
всего называют таблицу вида
|
|
y1 |
y2 |
... |
ym |
|
x1 |
p11 |
p12 |
... |
p1m |
|
x2 |
p12 |
p12 |
... |
p2m |
|
... |
... |
... |
pij |
... |
|
xn |
pn1 |
pn2 |
... |
pnm |
где
![]() и
и
![]() .
.
По
этой таблице можно найти распределения
![]() и
и
![]() компонент
x и h . Они вычисляются по формулам:
компонент
x и h . Они вычисляются по формулам:
![]() .
.
Функция распределения случайной величины. Её свойства
Каждая случайная величина полностью определяется своей функцией распределения.
Если .- случайная величина, то функция F(x) = F (x) = P( < x) называется функцией распределения случайной величины . Здесь P( < x) - вероятность того, что случайная величина принимает значение, меньшее x.
Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.
Функция распределения любой случайной величины обладает следующими свойствами:
-
F(x) определена на всей числовой прямой R;
-
F(x) не убывает, т.е. если x1
 x2,
то F(x1)
x2,
то F(x1) F(x2);
F(x2);
-
F(-
 )=0,
F(+
)=0,
F(+ )=1,
т.е.
)=1,
т.е.
 и
и
 ;
;
-
F(x) непрерывна справа, т.е.


