
- •1. Предмет теории вероятностей
- •Классическое определение вероятности
- •Геометрическое определение вероятности
- •Теорема сложения вероятностей и ее следствия
- •Условная вероятность
- •Теорема умножения вероятностей.
- •3. Формулы полной вероятности и формула Байеса
- •Определение
- •Свойства
- •Тождества
- •Числовые характеристики дискретных случайных величин
- •Зависимые и независимые случайные величины
- •Свойства
- •Свойства коэффициента корреляции
- •11. Числовые характеристики непрерывных случайных величин
- •Свойства
- •Определение
- •Свойства распределения Пуассона
- •Равномерное распределение.
- •Центральная предельная теорема Ляпунова.
- •Исправленная выборочная дисперсия
- •Определение
Свойства
Если
случайные величины X1
и X2
независимы и имеют нормальное распределение
с математическими ожиданиями μ1
и μ2
и дисперсиями
![]() и
и
![]() соответственно,
то X1
+ X2
также имеет нормальное распределение
с математическим ожиданием μ1
+ μ2
и дисперсией
соответственно,
то X1
+ X2
также имеет нормальное распределение
с математическим ожиданием μ1
+ μ2
и дисперсией
![]() .
.
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Определение
Выберем
фиксированное число
![]() и
определим дискретное
распределение,
задаваемое следующей функцией
вероятности:
и
определим дискретное
распределение,
задаваемое следующей функцией
вероятности:
![]() ,
,
где
-
 обозначает
факториал,
обозначает
факториал, -
 —
основание
натурального логарифма.
—
основание
натурального логарифма.
Тот
факт, что случайная величина
![]() имеет
распределение Пуассона с параметром
имеет
распределение Пуассона с параметром
![]() ,
записывается:
,
записывается:
![]() .
.
Свойства распределения Пуассона
-
Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть
 .
Тогда
.
Тогда
![]() .
.
-
Пусть
 ,
и
,
и
 .
Тогда условное
распределение
.
Тогда условное
распределение
 при
условии, что
при
условии, что
 ,
биномиально. Более точно:
,
биномиально. Более точно:
![]()
Равномерное распределение.
Пусть
плотность распределения случайной
величины является постоянной
![]() на интервале
на интервале
![]() ,
и
,
и
![]() вне этого интервала. Поскольку
вне этого интервала. Поскольку
 ,
то
,
то
![]() ,
откуда
,
откуда
![]()
![]() .
.
Таким образом, плотность распределения равномерного закона представляется в виде

![]()


b
![]()
![]()
Найдем математическое ожидание равномерного закона распределения.

Найдем дисперсию

![]()

![]()
13. Закон больших чисел.
теорема. Неравенство Чебышева.
Для любых случайных величин, имеющих ограниченную дисперсию, выполняется неравенство
![]()
(вероятность больших уклонений значений случайной величины от математического ожидания мала).
Доказательство.
Пусть p(x) − плотность вероятности случайной величины . Воспользуемся формулой для дисперсии случайной величины:

Вся
числовая прямая
![]() представляется в виде суммы двух
подмножеств: множества ,
для точек которого имеет место неравенство
представляется в виде суммы двух
подмножеств: множества ,
для точек которого имеет место неравенство
![]() ,
,
и
множества
![]() ,
для которого имеет место противоположное
неравенство
,
для которого имеет место противоположное
неравенство
![]()
В силу аддитивности интеграла по области интегрирования имеем оценку

Из определения следует, что
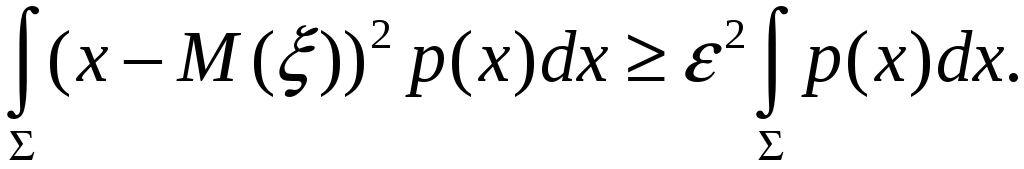
Следовательно,
![]()
Теперь вспомним правило нахождения вероятности попадания случайной величины на некоторое множество.
![]()
В частности,

Следовательно,
![]()
Теорема Чебышева (закон больших чисел).
Если
случайные величины
![]() независимы, одинаково распределены и
имеют конечную дисперсию, то среднее
арифметическое этих случайных величин
сходится по вероятности к их математическому
ожиданию.
независимы, одинаково распределены и
имеют конечную дисперсию, то среднее
арифметическое этих случайных величин
сходится по вероятности к их математическому
ожиданию.

(для
произвольного положительного числа
![]() вероятность любого, сколь угодно малого,
уклонения величины
вероятность любого, сколь угодно малого,
уклонения величины
 от M
стремится к 0 с ростом n).
от M
стремится к 0 с ростом n).
Сущность закона больших чисел в том, что среднее арифметическое большого числа случайных величин теряет случайный характер. Его значение можно предсказать. С большой вероятностью оно будет близко к среднему арифметическому их математических ожиданий.
Доказательство.
По теореме о математическом ожидании суммы, имеем

Для дисперсии получаем
![]()
В силу неравенства Чебышева получаем
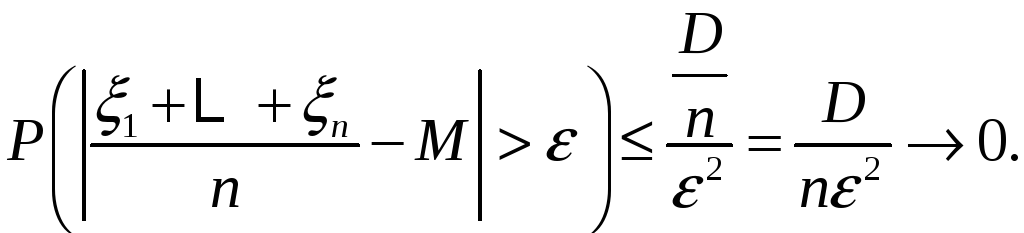
Ч.Т.Д.
