1. Идеалы.

Далее кольцо = «ассоциативное кольцо с единицей».

Определения.

Левым идеалом кольца А называется такое его подмножество a, которое

а) является подгруппой (аддитивной) группы кольца А, и

б) АaÍa (так как мы считаем 1ÎА, то Аa=a).

Определение правого идеала, отличается тем, что вместо АaÍa там требуется aАÍa.

Под Идеалом имеют ввиду двусторонний идеал, являющийся одновременно и правым и левым.

Упражнение 62.

Нулевой идеал =(0) – самый «маленький» идеал, он содержится во всех идеалах. Всё кольцо А – тоже идеал, оно содержит все идеалы. Возьмём какой-нибудь его элемент а и рассмотрим произведения его на все элементы кольца: I=Aa.

Проверьте, что I – левый идеал. Проверьте, что I=АаА –двусторонний идеал.

Идеалы I называются главными идеалами. Элемент а называется порождающим идеал аА, а идеал аА - порождённым элементом а. Коммутативное кольцо (с 0¹1), в котором все идеалы – главные, называется кольцом главных идеалов (КГИ).

Под суммой идеалов a+b понимают их сумму как (аддитивных) подгрупп кольца, а под их произведением a·b понимают множество всевозможных сумм вида х₁у₁+х₂у₂+…+х_ny_n, где x_iÎa, y_iÎb.

Упражнение 63.

Образует ли множество всех идеалов кольца кольцо? Есть ли в нём нейтральный элемент? Упражнение 64.

Пересечение любого (конечного или бесконечного) множества подгрупп – подгруппа, подколец – подкольцо и идеалов – идеал. Иными словами, все до сих пор встретившиеся нам алгебраические объекты замкнуты относительно операции пересечения.

Упражнение 65.

Пусть А₁ ÍA₂ Í ¼ Í A_nͼ-возрастающая цепочка (подгрупп, идеалов, подколец) в (группе, кольце). Тогда объединение всех входящих в неё (подгрупп, идеалов, подколец) А= - (подгруппа, идеал, подкольцо). Иными словами, все до сих пор встретившиеся нам алгебраические объекты замкнуты относительно операции объединения возрастающих цепочек.

Упражнение 66. Докажите, что a·bÍaÇb.

Упражнение 67. Пусть f:A®B – гомоморфизм колец. Тогда Kerf – идеал в А.

Пусть aÍА – идеал в кольце А. Превратим фактор-группу А/a в кольцо: произведением смежных классов a+a и b+a назовём класс a·b+a. Каковым в нём будет нейтральный элемент?

Упражнение 68.

Докажите, что это определение корректно и действительно превращает А/a в кольцо (называемое факторкольцом). Определите такой гомоморфизм колец А® А/a, ядром которого было бы a.

Тот естественный гомоморфизм, который вы определили, называется (как и в случае групп) каноническим. Таким образом, (как и в случае групп) ядро любого гомоморфизма колец – идеал и любой идеал является ядром некоторого гомоморфизма.

Упражнение 69*.

В КГИ любая возрастающая цепочка идеалов А₁ ÍA₂ Í ¼ Í A_nͼобрывается: начиная с некоторого номера n все идеалы оказываются совпадающими, а именно А_n=A_n+1=K(Про такую последовательность А₁, А₂, K,А_n,... говорят, что она стабилизируется начиная с индекса n.)

Область целостности А называется евклидовым кольцом если существует функция f: A\{0}®N такая, что"а, bÎA, b¹0 $q,rÎA такие, что a=bq+r ,причём (f(r)<f(b)) Ú (f(r)=0).

Кольца целых чисел Z и многочленов k[X] от одного переменного над полем k являются евклидовыми.

Для Z такой функцией f:Z®N является функция f(z)= .

Для кольца k[X] такой функцией является deg: k[X]\{0}®N ставящая каждому многочлену его степень. Упражнение 70*. Является ли k[[X]] (рядов Тейлора от одного переменного) евклидовым? Упражнение 71*. Евклидовы кольца являются кольцами главных идеалов.

Упражнение 72.

Как кольцо многочленов от любого числа переменных, так и кольцо степенных рядов от любого числа переменных, являются областями целостности.

Упражнение 73*. Кольцо многочленов от двух переменных уже не является КГИ.

Далее кольца предполагаются коммутативными.

Идеал a называется простым, если хуÎaÞ(хÎa)Ú(уÎa). Эквивалентное определение:

Упражнение 74. a прост Û А/a - область целостности.

Идеал a называется максимальным, если он не совпадает со всем кольцом и в то же время его не содержит никакой другой идеал в качестве собственного подмножества.

Упражнение 75*. Всякий максимальный идеал прост.

(hint: if xÏa, then Ax+aÉaÞ Ax+a=AÞax+m=1Þaxy+my=y)

Эквивалентное определение:

Упражнение 76. a максимален Û А/a - поле.

Далее везде (до отмены) А – область целостности (ОЦ).

Элемент а¹0 называется неприводимым, если он необратим (ÏА*) и а=b·cÞ(bÎA*)Ú(cÎA*).

Упражнение 77. Пусть р неприводим, а u – обратим. Þ u·p – тоже неприводим.

Упражнение 78. Элементы а и b порождают один и тот же идеал Û $ обратимый u, такой, что b=ua.

Упражнение 79*. Главный идеал (а) прост Þ элемент а неприводим.

Def. Говорят, что элемент а¹0 обладает однозначным разложением на неприводимые элементы, если:

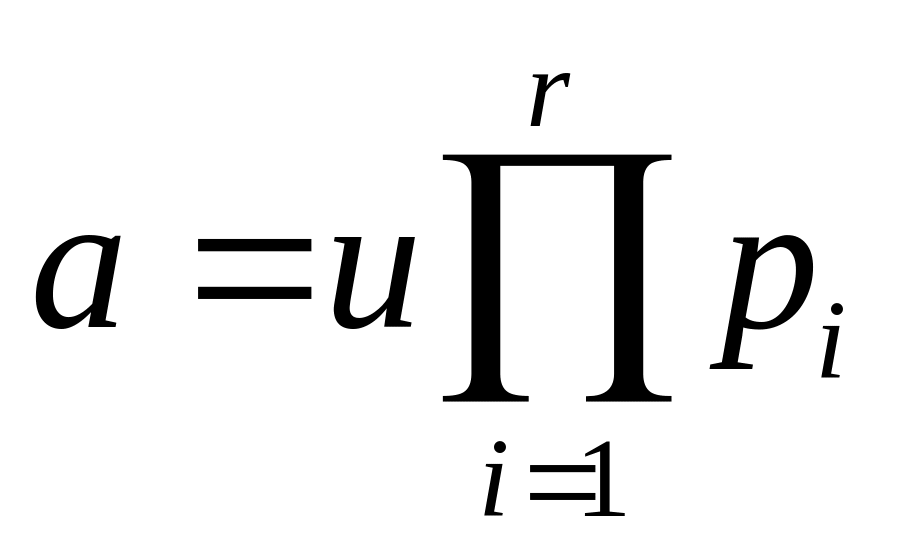• , где uÎA*, а p_i неприводимы и

• для любых двух таких разложений = 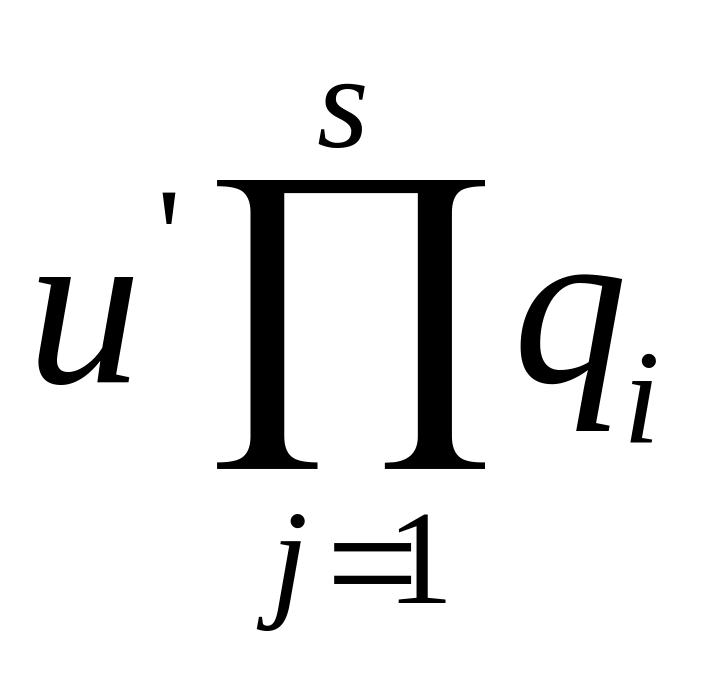r=s и после перестановки индексов p_i=u_iq_i, где u_i- обратимые.

Def. Кольцо называется факториальным, если оно есть область целостности (ОЦ) и всякий ¹0 его элемент обладает однозначным разложением на неприводимые элементы.

Говорят, что а делит b (является делителем b; b делится на а) и пишут aïb или b┆a, если b=ac для некоторого с.

Элемент d называется НОД(a,b), если dïа, dïb и (еïа)Ù(еïb)Þ(еïd) (т.е., любой другой общий делитель а и b является также и делителем d).