2. Действие групп на множествах.

Мы рассмотрели множество с одной бинарной операцией и определёнными требованиями к этой операции, назвали множество, наделённое такой операцией группой. В дальнейшем нам предстоит познакомиться с множествами, наделёнными двумя согласованными операциями, а также с множествами, наделёнными иными структурами (например, с выделенными определёнными системами подмножеств) и т.д. Все эти различные категории объектов (множества + структуры в них) имеют соответствующие названия и обладают морфизмами, согласованными с этими структурами и изучаются по приблизительно одной схеме: сначала определяются простейшие объекты в данной категории, а потом на их основе классифицируются (по возможности!) и остальные. Наряду с этим рассматриваются и пары объектов различных категорий, взаимодействующих друг с другом. Сейчас мы познакомимся с одной такой парочкой: (G,M), где G – группа, а М – множество.

Def. Действием (слева) группы G на множестве М называется отображение f: GMM при котором f(e,m)=m mM и f(gh,m)=f(g,f(h,m)) g,hG, mM. Удобно изображать образ пары (х,m) при отображении f как xm. Тогда условия действия G на М можно переписать лаконичнее и нагляднее:

а) em=m

b) (gh)m=g(hm)

Говорят также, что M есть G –множество.

Фиксируем элемент gÎG. Возникает отображение g*:MM; g*(m)=gm.

Упражнение №29.

Докажите, что отображение g* - автоморфизм (перестановка) множества М.

Таким образом, возникает отображение групп: *: G ®AutM; g ®g*.

Упражнение №30.

Докажите, что отображение * - гомоморфизм групп.

Примеры.

Фиксируем некоторый элемент gG и определим g*: G®G формулой g(h)=ghg^-1.

Упражнение №31.

Докажите, что отображение g* - автоморфизм группы G.

Упражнение №32.

Докажите, что, определяя так g* для каждого gÎG, получим действие G на самой себе. Это действие называется действием посредством сопряжений:

Упражнение №33.

Докажите, что посредством сопряжений G действует также на множестве своих подмножеств.

Упражнение №34.

Докажите, что посредством сопряжений G действует также на множестве своих подгрупп.

Упражнение №35.

Пусть M есть G –множество. Фиксируем некоторый элемент mM и рассмотрим подмножество G_mG, G_m=gÎG  gm=m. Проще говоря, это те элементы группы G, которые оставляют элемент m на месте (не перемещают его).

Проверьте, что G_m – подгруппа группы G.

Def. G_m называется группой изотропии элемента m, а также стабилизатором или стационарной подгруппой элемента m.

Def. Подмножество М, состоящее из всех gm, gÎG, обозначается как Gm и называется орбитой элемента m (относительно группы G).

Упражнение №36.

Докажите, что группы изотропии элементов, принадлежащих одной орбите, сопряжены.

Примеры. (Упражнение №37.)

Найдите, что собой будут представлять орбиты и группы изотропии различных точек (элементов) в следующих примерах. Во всех примерах в качестве G-множества М выступает плоскость, а в качестве группы G выступают:

1. группа всех параллельных переносов;

2. подгруппа этой группы: группа всех параллельных переносов вдоль фиксированного вектора (направления), т.е., параллельно заданной прямой;

3. подгруппа этой группы: группа всех параллельных переносов вдоль фиксированного вектора, кратных данному вектору (если вектор-стрелку обозначим 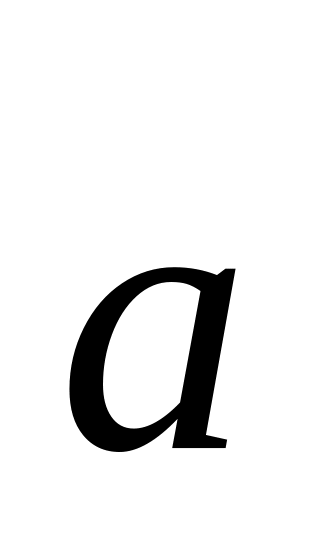; то наши переносы образуют группу Z );

4. группа всех параллельных переносов вдоль двух фиксированных векторов, кратных данным векторам (если вектора обозначим и 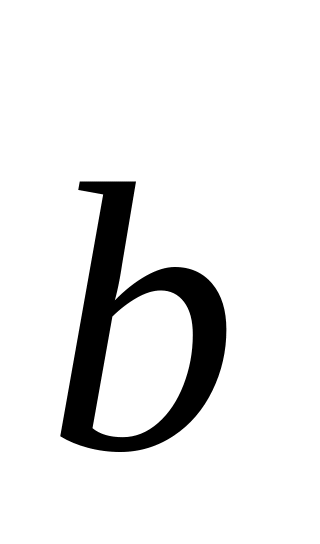; то наши переносы образуют группу Z +Z );

5. Группа всех гомотетий с центром в данной выделенной точке О и коэффициентами в Q\{0};

6. Подгруппа этой группы: группа всех гомотетий с коэффициентами в Q⁺;

7. Группа всех поворотов плоскости с центром в данной выделенной точке О;

8. *Подгруппа этой группы: группа всех поворотов плоскости кратных данному углу поворота .

После выполнения этого упражнения становится понятным происхождения термина «орбита». Все вышеназванные группы действуют также и на множестве всех подмножеств плоскости (в частности, треугольниках, четырехугольниках, многоугольниках, окружностях и их дугах, фигурах, образованных замкнутыми, не самопересекающимися кривыми, и т.д.). Как называются орбиты, например, треугольников относительно группы, порождённой всеми параллельными переносами, симметриями относительно всевозможных прямых, проходящих через одну точку и поворотов вокруг этой же точки? Если добавить к вышеназванным преобразованиям ещё и гомотетии (относительно той же точки), то получим разбиение множества всех треугольников на орбиты подобных треугольников.

Упражнение 38.

Докажите, что различные орбиты не пересекаются и, вообще, действие G разбивает все

G-множество М на орбиты. Следовательно, можно написать:

, где I –некоторое множество индексов, а m_i –элементы различных орбит.

Упражнение 39*.

Пусть mM, G_mG – подгруппа изотропии элемента m. Докажите, что длина (порядок) орбиты элемента m совпадает с индексом (G:G_m). В частности, поскольку группа действует на множестве своих подгрупп посредством сопряжения, то

Упражнение 40.

число сопряжённых с Н подгрупп G равно индексу нормализатора N_H в G.

Если G-множество М конечно, то упражнение 10 даёт формулу для порядка (числа элементов) множества М как суммы порядков орбит действия группы G:

(формула разложения на орбиты)

В случае, когда конечная группа действует на себе посредством сопряжений, получаем отсюда формулу классов: где С- множество представителей различных классов сопряжённых элементов.

3. Rings. First acquaintance.

1. Definitions, samples.

Теперь мы познакомимся с ещё одним алгебраическим объектом – кольцами.

Это множество уже с двумя операциями. Относительно одной из них, записываемой аддитивно и называемой поэтому «сложением», оно – абелева² группа. А вторая операция, называемая умножением, связана с первой дистрибутивным законом:

a(b+c)=ab+ac и (b+c)a=ba+bc

Далее, в зависимости от свойств умножения, кольца бывают, соответственно:

ассоциативными, коммутативными, с единицей (или без) и т.д. Все кольца, о которых пойдёт речь в этом тексте – ассоциативные и с единицей.

Вообще говоря, множество с ассоциативной операцией (и всё) называется полугруппой, полугруппа с единичным (нейтральным) элементом – моноидом. Таким образом, группа – это моноид, в котором все элементы обратимы (имеют обратные к себе). Моноиды тоже могут быть коммутативными (или не быть). Мы будем заниматься ассоциативными кольцами с единицей, и, как правило, коммутативными. То есть, такими, которые относительно операции умножения образуют коммутативный моноид с единицей. Нейтральный элемент по сложению называется, естественно нулём. Обратный по сложению к элементу х обозначим, как обычно, как –х, а по умножению, если он имеется, как х^-1.

Упражнение 41.

Докажите, что 0·х=х·0=0 "х из кольца. (hint: check it is neutral regarding x)

Упражнение 42.

Докажите, что у нуля не может быть обратного (по умножению).

Упражнение 43.

Имеет место: (-х)·у=-(х·у); (-х)·(-у)=х·у "х,у из кольца.

Определение. Если у всех, (кроме, естественно, нуля), элементов кольца обратные всё-таки есть, то такое кольцо называется телом.

Если это тело к тому же ещё и коммутативно, то оно называется полем.

Если a·b=0 и при этом a¹0, b¹0, то элементы a и b называются делителями нуля.

Упражнение 44. Делители нуля не обратимы (не имеют обратных элементов).

Рассмотрим подмножество А* кольца А, состоящее из всех его обратимых элементов.

Упражнение 45. А* является группой относительно умножения в кольце.

Эта группа называется группой единиц кольца.

Кольцо без делителей нуля называется целостным кольцом. Если оно при этом ещё и коммутативно, то оно называется областью целостности.

Упражнение 46.

Докажите, что в целостном кольце действуют законы сокращения: аb=ас Þ b=c; bа=са Þ b=c.

Подкольцом, естественно, называется подмножество кольца, которое само является кольцом относительно операций + и ´ кольца. То есть, оно должно быть замкнуто относительно обеих этих операций, содержать 0 и 1 и противоположные ко всем своим элементам (т.е., быть замкнутым ещё и относительно взятия обратного по сложению элемента).

Гомоморфизм колец определяется естественным образом: помимо того, что он должен быть гомоморфизмом (абелевых) групп, он должен точно так же быть перестановочен с операцией умножения: f(a·b)=f(a)·f(b).

Упражнение 47.

Гомоморфный образ кольца – кольцо. При этом образом 1 будет вновь единица (образа).

Примеры колец.

Простейшим и главным, конечно, является кольцо Z. Являются также кольцами (конечными!) и кольца классов вычетов по модулю m: Z/mZ.

Упражнение 48. Кто в них играет роль нуля, а кто – единицы?

При каких m кольцо Z/mZ окажется полем?

Кольца многочленов от нескольких переменных с целыми коэффициентами – Z[X,Y,...,W] или рациональными коэффициентами - Q[X,Y,...,W]; вообще с коэффициентами из некоторого кольца К: К[X,Y,...,W]. Хотя в каждом из многочленов этих колец используется лишь конечное число символов X,Y,...,W, общее же множество этих символов быть бесконечным множеством. Нам, конечно, в первую очередь будет важен тот частный случай, когда символ лишь один: кольцо многочленов от одной переменной К[X].

Ряды Тейлора.

Рассмотрим формальный степенной ряд p(X)= .

Он отличается от многочлена только тем, что в нём «бесконечное количество» слагаемых. Мы воспринимаем его не как результат выполнения какой-то операции, не как некую функцию от переменной Х, а просто как некое алгебраическое выражение. Потому и называется он «формальным». С такими выражениями легко определяются как операция сложения, так и операция умножения, после чего они превращаются в кольцо. Ну, складываем их, разумеется, почленно: приводим подобные члены, складываем коэффициенты при одинаковых степенях Х. Да и умножаем, как многочлены: коэффициент при любой степени произведения зависит лишь от конечной суммы произведений коэффициентов сомножителей. Коэффициенты ряда берутся при этом из некоторого поля k (например, поля Q).

Упражнение 49.

Найдите, например, первые пять членов произведения рядов А(Х)=1-Х+Х²-Х³+…и В(Х)=Х-2Х³+3Х⁵-….

Упражнение 50.

Напишите общую формулу для коэффициента c_n при степени Хⁿ произведения ряда p(X)= и ряда q(X)= .

Это кольцо рядов от одной переменной с коэффициентами в некотором поле k называется кольцом рядов Тейлора и обозначается k[[X]]. Двойные квадратные скобки, в отличие от одинарных, указывают на то, что речь идёт не о многочленах, а о рядах. Многочлены, являются, однако, частным случаем рядов Тейлора: а именно, рядов, в которых число ненулевых слагаемых конечно. Они являются подкольцом в кольце рядов.

Упражнение 51. Докажите ассоциативность умножения рядов. (Это хорошее упражнение на работу с индексами).

Упражнение 52.

Какой ряд играет роль нейтрального элемента по умножению?

* Найдите ряд, обратный ряду Р(Х)= .

Далее везде считаем ноль натуральным числом, присоединяем его к натуральному ряду. Если коэффициенты рядов или многочленов берутся из какого-то поля k, то говорят о кольце (рядов или многочленов) над полем k. Для кольца формальных степенных рядов (от одного переменного) k[[X]] над полем k определим функцию f:k[[X]]\{0}®N называемую нижняя степень ряда как степень первого отличного от нуля члена ряда. Нулевому ряду (равно как и нулевому многочлену) сопоставим символ -∞ определив для него операцию сложения с целыми числами как - ∞+n=-∞ и отношение - ∞<n "nÎZ.

Упражнение 53*.

В кольце многочленов обратимыми являются многочлены нулевой степени, и только они.

В кольце же рядов обратимыми являются все ряды нулевой нижней степени. (Это условие является как достаточным, так и необходимым).

Можно рассматривать и ряды от нескольких переменных – бесконечных сумм вида å , где все индексы i_jÎN; 1£j£n.

Множество символов (Х₁, Х₂,…,Х_n,…) может быть и бесконечным (и даже несчётным!). Для удобства записи таких сумм используются обозначения где Х=(Х₁,Х₂,…Х_n), a a=(a₁,a₂,...,a_n) – так называемый мультииндекс.

Определим .

Тогда степенью многочлена от нескольких переменных будет служить , а нижней степенью ряда от нескольких переменных будет служить .

Ряды Лорана.

Ряды вида Р(X)= где nÎZ, т.е. ряды, в которых допускаются и члены с отрицательными степенями переменной называются лорановскими рядами.

Упражнение 54*. Кольцо рядов Лорана (от одной переменной) является полем.

Квадратные матрицы.

Квадратной матрицей второго порядка А=(a_i,j), i,j=1,2 называется таблица из двух строк и двух столбцов: А=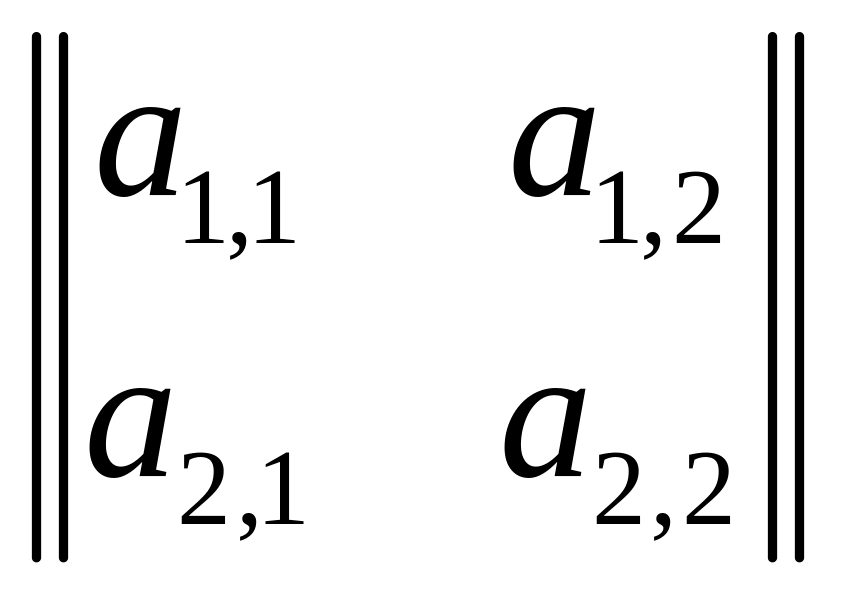 . Все четыре элемента, составляющие матрицу называются её компонентами и берутся из одного и того же поля (например, Q).

Сложение двух таких матриц определяется покомпонентно: если А=(a_i,j) и В=(b_i,j), то А+В=С, где С=(с_i,j), с_i,j=а_i,j+b_i,j. Точно также определяется сложение матриц любого порядка.

Упражнение 55.

Проверьте, является ли множество квадратных матриц абелевой группой по сложению.

Умножение же определяется так: элемент с_i,j произведения, стоящий на пересечении i–ой строки и j–го столбца, является их произведением (строки на столбец). А произведение строки на столбец определяется как сумма произведений их первых элементов, вторых элементов,…, последних элементов: a_i,1·b_1,j+ a_i,2·b_2,j+...+ a_i,n·b_n,j. Например, произведение строки элементов а_i=(1,-1,0,3) на столбец элементов b_j=(0,2,-4,1) будет элементом

с_i,j=1·0+-1·2+0·-4+3·1=1.

Упражнение 56*.

Проверьте, является ли множество квадратных матриц кольцом. Наибольшую трудность у вас вызовет проверка ассоциативности. Эта проверка - хорошее упражнение на работу с индексами. Будет ли это кольцо коммутативным? Кто является нейтральным элементом по умножению?

Упражнение 57*.

Найдите центр кольца квадратных матриц – множество матриц, коммутирующих (перестановочных) со всеми матрицами этого кольца.

Упражнение 58*.

Всякая ли матрица второго порядка обратима в кольце матриц?

Выражение, которое у вас получилось при решении упражнения 16, (неравенство нулю которого явилось условием обратимости матрицы), называется определителем матрицы второго порядка. Обозначается: det(A).

Упражнение 59*.

Докажите, что det(A×B)=det(A) det(B) " A,B.

Упражнение 60.

Пусть R –кольцо, М- множество, А(M,R) – множество всех отображений M в R. Определите операции в А так, чтобы оно относительно этих операций превратилось в кольцо.

Упражнение 61.

Пусть М- абелева группа и А=End(M) – множество её эндоморфизмов. Определите операции в А так, чтобы оно относительно этих операций превратилось в кольцо.