27. *Теорема Тейлора

Формула Тейлора для многочлена

Пусть дан некоторый многочлен  -й степени (с действительными коэффициентами) 

Зададим произвольное   и проведем преобразования, заменив   на  . Получим 

Собрав подобные члены при одинаковых степенях, находим 

Это есть разложение многочлена   по степеням разности  . Дифференцируя его по  , получим 

Итак, вычислены коэффициенты 

Следовательно, многочлен   можно представить в виде

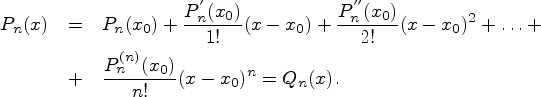
Это есть формула Тейлора для многочлена   в окрестности точки  .   -- многочлен Тейлора степени   от функции  . Если степень многочлена Тейлора для   есть  , то 

Формула Тейлора. Пусть на интервале [a, b] функция f(x) дифференцируема n раз и выполняются следующие равенства:f(a) = f(b) = f '(a) = f ''(a)= ... = f ^(n-1)(a)=0

Тогда внутри интервала [a, b] найдется хотя бы одно значение с, при котором f ⁽ⁿ⁾(c) = 0

   Доказательство. По теореме Ролля имеем f '(x₀ ) = 0,

где a < x₀ < b. Тогда f '(x) на интервале [a, x₀] удовлетворяет теореме Ролля, так как, по условию, f '(a) = 0 и f '(x₀ ) = 0, а потому f ''(x₁ ) = 0, где a < x₁ < x₀.    Применяя теорему Ролля последовательно к функциям f ''(x), f '''(x), ..., f ^(n-1)(x), найдем наконец:

f ⁽ⁿ⁾(с) = 0,

где a < c < x_n-1 < b . Теорема доказана.    Выведем теперь формулу Тейлора с остаточным членом в форме Лагранжа.    Пусть функция f (x) дифференцируема n раз на интервале [a, b].    Рассмотрим вспомогательную функцию

(x) = f (x) - P (x),

где

   Продифференцируем n раз функцию (x). Тогда будем иметь

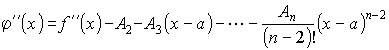. . . . . . . . . . . . . . . . . . . . . . . . . . . . ^(n-1)(x) = f^(n-1)(x) - A_n-1 - A_n(x - a), ⁽ⁿ⁾(x) = f⁽ⁿ⁾(x) - A_n

   Потребуем, чтобы функция (x) удовлетворяла условиям обобщенной теоремы Ролля. Тогда будем иметь

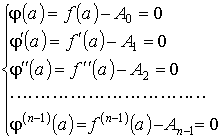     (1) .

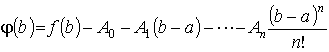   Так как функция (x) удовлетворяет условиям обобщенной теоремы Ролля, то найдется такое значение с (a < c < b), что

⁽ⁿ⁾(с) = f⁽ⁿ⁾(с) - A_n = 0     (2)

   Далее найдем из n первых уравнений системы (1) коэффициенты A₀ , A₁ , ..., A_n-1:

A₀ = f(a), A₁ = f'(a), A₂ = f''(a), ..., A_n-1 = f^(n-1)(a),

а из уравнения (2) коэффициент A_n: A_n = f⁽ⁿ⁾(c) и подставим их значения в последнее уравнение системы (1):

,

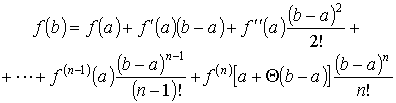где 0 <  < 1    Заменяя b на x, получим формулу Тейлора:

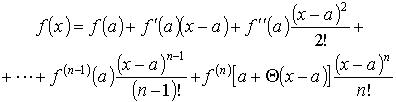
где 0 <  < 1    Последнее слагаемое

называется остаточным членом в форме Лагранжа.    При a = 0 получается так называемая формула Маклорена:

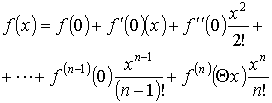
где 0 <  < 1, а остаточный член записывается в виде

28. Достаточные условия экстремума

Напомним, что экстремум функции – это ее локальный максимум или минимум.

1. Случай функции одной переменной. Заметим, что максимум или минимум дифференцируемой функции может находиться лишь в ее критической точке (необходимое условие экстремума).

Пусть х₀ – критическая (стационарная) точка функции y = f(x) (т.е. внутренняя точка области ее определения, в которой производная равна нулю). Тогда можно сформулировать следующие достаточные условия существования экстремума в этой точке:

а) Пусть функция дифференцируема в некоторой  окрестности U точки х₀, не содержащей других критических точек. Тогда:

   если при переходе через точку х₀ производная f ' меняет свой знак с плюса на минус, х₀ – точка (локального) максимума функции;

   если при переходе через точку х₀ производная меняет свой знак с минуса на плюс, х₀ – точка (локального) минимума функции;

   если при переходе через точку х₀ производная не меняет свой знак, в точке х₀нет экстремума.

б) Пусть в точке х₀ существует вторая производная функции f,  f ''(x0), не равная нулю. Тогда:

   если f’’(x₀) > ₀, х₀ – точка (локального) минимума функции;

   если f’’(x₀) < ₀, х₀ – точка (локального) максимума функции.

 в) Пусть в точке х₀ функция дифференцируема n раз, причем   а f⁽ⁿ⁾(x₀) ≠ 0. Тогда:

–   если n четно и f⁽ⁿ⁾(x₀) < 0, то х₀ – точка (локального) максимума функции;

–   если n четно и f⁽ⁿ⁾(x₀) > 0, то х₀ – точка (локального) минимума функции;

–   если n нечетно, в точке х₀ нет экстремума.

Конечно, в любой ситуации применяется наиболее удобный признак.

2. Случай функции двух переменных. Пусть функция двух переменных z = f(x; y) дифференцируема в некоторой окрестности точки М(х₀; у₀), дважды дифференцируема в самой точке М и при этом точка М – стационарная (критическая), т.е. полный дифференциал функции в этой точке равен нулю (что эквивалентно равенству нулю обеих частных производных функции, z'_x и z'_y, в этой точке).

Введем следующие обозначения: Тогда:

–   если АС – В² > 0, то функция имеет в точке М локальный экстремум, причем в случае А > 0 минимум, а при A < 0 – максимум;

–   если  АС – В² < 0, в точке М экстремума нет;

–   случай АС – В² = 0 требует дополнительного исследования.

Достаточное условие экстремума: Если при переходе через стационарную точку производная меняет знак, то эта точка является экстремумом. Если меняет знак с «+» на «-», то это точка максимума. Если меняет знак с «-» на «+», то это точка минимума.