
- •Единственность предела сходящейся последовательности
- •Ограниченность сходящейся последовательности
- •Свойства бесконечно малых последовательностей.
- •Арифметические свойства сходящихся последовательностей.
- •Теорема Кантора о вложенных отрезках
- •Теорема Больцано-Вейерштрасса об ограниченных последовательностях.
- •Критерий Коши сходимости последовательности.
- •*Теорема о существовании точных границ числовых множеств.
- •*Принцип Бореля-Лебега
- •*Теорема Больцано-Вейерштрасса о существовании предельной точки у ограниченного числового множества
- •Эквивалентность 2х определений предела функции в точке
- •*Критерий Коши предела функции в точке
- •Непрерывность сложной функции
- •Теоремы Вейерштрасса для непрерывных функций на отрезке
- •Теорема Больцано-Коши о нулях функции
- •*Теорема о существовании обратной функции
- •*Теорема о существовании и непрерывности обратной функции
- •Непрерывность дифференцируемой функции
- •Доказательство
- •Производная и дифференцируемость функции в точке
- •Дифференцируемость функции в точке: правила дифференцирования, дифференцируемость сложной функции
- •Правила дифференцирования
- •25. Теоремы о среднем: Ферма, Ролля, Лагранжа, Коши Теоремы Ферма и Ролля.
- •Теоремы Коши и Лагранжа.
- •26. Правила Лопиталя
- •27. *Теорема Тейлора
- •28. Достаточные условия экстремума
- •29. Точки возрастания функции и второе достаточное условия экстремума функции в точке
Критерий Коши сходимости последовательности.
Теорема 4.4.1 (критерий Коши). Для того чтобы последовательность сходилась, необходимо и достаточно, чтобы она была фундаментальной.
Доказательство.
Необходимость (метод ![]() ).
Пусть
).
Пусть ![]() при
.
Тогда для любого
существует
номер
такой,
что для любых
при
.
Тогда для любого
существует
номер
такой,
что для любых ![]() выполняются
неравенства
выполняются
неравенства ![]()
![]() .
Рассмотрим цепочку соотношений
.
Рассмотрим цепочку соотношений
![]()
что означает, что фундаментальна.
Достаточность. Докажем
сначала ограниченность последовательности
.
Возьмем ![]() ,
тогда, в силу фундаментальности
,
найдется номер
такой,
что для всех
выполняется
,
тогда, в силу фундаментальности
,
найдется номер
такой,
что для всех
выполняется ![]() .
Следовательно,
.
Следовательно, ![]() ,
поэтому
,
поэтому ![]() .
Итак, для всех
.
Итак, для всех ![]() при
фиксированном
при
фиксированном ![]() выполняется
,
что означает ограниченность
последовательности
(см.
замечание 3.2.1). По теореме
4.3.2 из последовательности
можно
выделить подпоследовательность
выполняется
,
что означает ограниченность
последовательности
(см.
замечание 3.2.1). По теореме
4.3.2 из последовательности
можно
выделить подпоследовательность ![]() ,
сходящуюся к некоторому числу
.
,
сходящуюся к некоторому числу
.
Докажем,
что и вся последовательность
сходится
к числу
.
Возьмем любое
,
тогда найдется номер
(из фундаментальности
)
такой, что для всех ![]() выполняется
выполняется ![]() .
Ввиду сходимости
.
Ввиду сходимости ![]() при
,
по взятому
найдется
номер
при
,
по взятому
найдется
номер ![]() такой,
что
такой,
что ![]() и
и
![]() .
Тогда для нашего
.
Тогда для нашего
![]()
![]()
что означает сходимость последовательности к числу .
*Теорема о существовании точных границ числовых множеств.
Если непустое множество действительных чисел ограничено сверху, то существует точная верхняя граница этого множества.
Доказательство (метод
Больцано -- метод деления отрезка
пополам). Пусть ![]() и
множество
и
множество ![]() ограничено
сверху числом
ограничено
сверху числом ![]() .
Рассмотрим отрезок
.
Рассмотрим отрезок ![]() ,
заметим, что правее
нет
точек из
.
Разделим отрезок на два равных отрезка
и обозначим
самый
правый из них, содержащий хотя бы одну
точку из
,
т. е. правее
нет
точек из
.
Так же поступим с отрезком
,
получим отрезок
,
содержащий хотя бы одну точку из
,
правее которого нет точек из
.
Продолжив этот процесс по индукции,
получим последовательность отрезков
,
заметим, что правее
нет
точек из
.
Разделим отрезок на два равных отрезка
и обозначим
самый
правый из них, содержащий хотя бы одну
точку из
,
т. е. правее
нет
точек из
.
Так же поступим с отрезком
,
получим отрезок
,
содержащий хотя бы одну точку из
,
правее которого нет точек из
.
Продолжив этот процесс по индукции,
получим последовательность отрезков ![]() ,
длины которых
,
длины которых ![]() .
При этом при любом
правее
нет
точек из
.
На основании принципа вложенных
отрезков (теорема
4.1.1) существует
единственная точка
.
При этом при любом
правее
нет
точек из
.
На основании принципа вложенных
отрезков (теорема
4.1.1) существует
единственная точка ![]() ,
лежащая во всех отрезках системы
.
,
лежащая во всех отрезках системы
.
Докажем,
что ![]() .
В самом деле, по построению для всех
.
В самом деле, по построению для всех ![]() и
для всех
выполняется
неравенство
и
для всех
выполняется
неравенство ![]() .
Тогда, переходя к пределу в этом
неравенстве при
,
получим (используя то, что
.
Тогда, переходя к пределу в этом
неравенстве при
,
получим (используя то, что ![]() )
неравенство
)
неравенство ![]() .
Возьмем теперь любое
.
Тогда (так как и
.
Возьмем теперь любое
.
Тогда (так как и ![]() )
существует номер
такой,
что
)
существует номер
такой,
что ![]() лежит
левее отрезка
.
При этом в
лежит
хотя бы одна точка
лежит
левее отрезка
.
При этом в
лежит
хотя бы одна точка ![]() ,
т.е. выполняется неравенство
,
т.е. выполняется неравенство ![]() .
Следовательно,
.
.
Следовательно,
.
Будем
считать в дальнейшем, что если
множество
неограничено
сверху, то ![]() ,
если неограничено снизу, то
,
если неограничено снизу, то ![]() .
.
*Принцип Бореля-Лебега
Лемма о конечном покрытии (принцип Бореля-Лебега).
В любой системе интервалов, покрывающих отрезок, имеется конечная подсистема, покрывающая этот отрезок.
Доказательство:
Рассмотрим отрезок
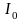 =
[a,b]. S = {U}- система интервалов U, его
покрывающая. Допустим нельзя выделить
конечную подсистему, покрывающую данный
отрезок. Поделим
пополам. Одна из его половин не допускает
конечного подпокрытия. Обозначим его
=
[a,b]. S = {U}- система интервалов U, его
покрывающая. Допустим нельзя выделить
конечную подсистему, покрывающую данный
отрезок. Поделим
пополам. Одна из его половин не допускает
конечного подпокрытия. Обозначим его
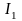 .
Проделаем то же с отрезком
,
получим
.
Проделаем то же с отрезком
,
получим
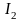 и
так далее. Получаем последовательность
вложенных отрезков
и
так далее. Получаем последовательность
вложенных отрезков
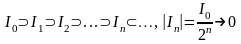 .
.
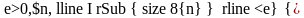 по
лемме о вложенных отрезках получаем:
по
лемме о вложенных отрезках получаем:
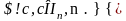 Так
как
Так
как
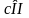 ,
то в S
,
то в S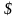 интервал
интервал
 ,
такой что
,
такой что
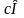 .
Обозначим
.
Обозначим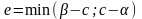 .
.
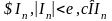 .
.
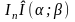 -
противоречие :
-
противоречие :
С
одной стороны
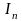 -
не допускает конечного покрытия, а с
другой стороны указан конечный интервал
∈
-
не допускает конечного покрытия, а с
другой стороны указан конечный интервал
∈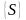 ,
который покрывает отрезок
.
,
который покрывает отрезок
.
