25. Теоремы о среднем: Ферма, Ролля, Лагранжа, Коши Теоремы Ферма и Ролля.

 Теорема 1. Если переменная величина принимает только неотрицательные значения (y=f(x)0), то ее предел (если он существует) не может быть числом отрицательным.

Теорема 2. Если переменная величина принимает только неположительные значения (y=f(x)0), то ее предел (если он существует) не может быть числом положительным.

Теорема  3. Если переменная величина имеет предел, отличный от нуля, то начиная с некоторого момента, она принимает значения только того знака, каков знак ее предела.

Теорема Ферма. (Ферма, 1601-1665 – французский математик).

Пусть функция f(x), определенная в интервале (a, b), принимает в некоторой точке x=c этого интервала наибольшее или наименьшее значение.

В таком случае, если в точке x=c существует производная этой функции, то она равна нулю.

Доказательство. Пусть f(с)=M, где М – наибольшее значение функции в интервале (a, b). Покажем, что f^/(c)=0. По определению производной:    f^/(c)= .

     Так как в точке x=c функция принимает наибольшее значение, то при любом знаке x имеем: f(c)f(c+x) и f(c+x)-f(c)0

Отсюда, если x>0, то   и по теореме 2 имеем: f^/(c)=  .

Если же x<0, то   и f^/(c)= .

Сравнивая полученные для f^/(c) неравенства видим, что оба они удовлетворяются только тогда, когда f^/(c)=0, что и требовалось доказать. Геометрический смысл теоремы Ферма: касательная к графику функции y=f(x) в точке экстремума, в которой функция дифференцируема, параллельна оси Ox (так как y^/=tg=0), =0.

Теорема Ролля (Ролль, 1652-1719 – французский математик).

     Если функция f(x) непрерывна на сегменте [a, b], дифференцируема во всех его внутренних точках и на концах сегмента обращается в нуль, то есть f(a)=f(b)=0, то ее производнаяf^/(x) обращается в нуль хотя бы в одной внутренней точке x=c этого сегмента.

Доказательство. Так как функция непрерывна на сегменте, то она достигает на этом сегменте своего наибольшего М и наименьшего значения m (смотри свойства функций, непрерывных на сегменте).

     Если M=m, то функция постоянна на сегменте [a, b] и, следовательно, f^/(x)=0 в любой точке этого сегмента.

     Пусть Mm, тогда одно из этих чисел, например, M0. Поэтому, если наибольшее значение М достигается в точке c: f(c)=M, то точка с должна быть внутренней точкой сегмента [a,b], то есть должна принадлежать интервалу (a, b) (так как на концах сегмента f(a)=f(b)=0).

     Следовательно, по теореме Ферма f^/(c)=0.

Замечание. Теорема Ролля верна и в том случае, если f(a)=f(b)0. 

Геометрический смысл.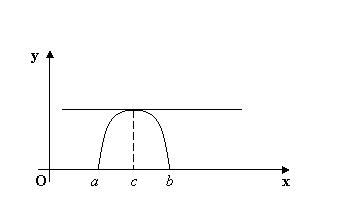      Если график непрерывной на сегменте [a, b] и дифференцируемой внутри него функции пересекает ось Ox в двух точках x=a и x=b, то между этими точками найдется хотя бы одна точка с, a<c<b, в которой касательная к графику параллельна оси абсцисс. 

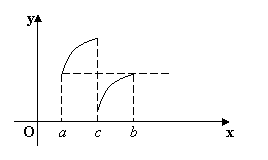Замечание. Нарушение хотя бы одного из условий теоремы Ролля может привести к тому, что для соответствующей функции заключение теоремы не будет справедливо. 

(здесь нарушена непрерывность внутри отрезка [a, b]).