
- •Единственность предела сходящейся последовательности
- •Ограниченность сходящейся последовательности
- •Свойства бесконечно малых последовательностей.
- •Арифметические свойства сходящихся последовательностей.
- •Теорема Кантора о вложенных отрезках
- •Теорема Больцано-Вейерштрасса об ограниченных последовательностях.
- •Критерий Коши сходимости последовательности.
- •*Теорема о существовании точных границ числовых множеств.
- •*Принцип Бореля-Лебега
- •*Теорема Больцано-Вейерштрасса о существовании предельной точки у ограниченного числового множества
- •Эквивалентность 2х определений предела функции в точке
- •*Критерий Коши предела функции в точке
- •Непрерывность сложной функции
- •Теоремы Вейерштрасса для непрерывных функций на отрезке
- •Теорема Больцано-Коши о нулях функции
- •*Теорема о существовании обратной функции
- •*Теорема о существовании и непрерывности обратной функции
- •Непрерывность дифференцируемой функции
- •Доказательство
- •Производная и дифференцируемость функции в точке
- •Дифференцируемость функции в точке: правила дифференцирования, дифференцируемость сложной функции
- •Правила дифференцирования
- •25. Теоремы о среднем: Ферма, Ролля, Лагранжа, Коши Теоремы Ферма и Ролля.
- •Теоремы Коши и Лагранжа.
- •26. Правила Лопиталя
- •27. *Теорема Тейлора
- •28. Достаточные условия экстремума
- •29. Точки возрастания функции и второе достаточное условия экстремума функции в точке
Арифметические свойства сходящихся последовательностей.
Свойство
3.4.1. Если
последовательности
и ![]() сходятся,
то сходится последовательность
сходятся,
то сходится последовательность
![]() и
и ![]()
Свойство
3.4.2. Если
последовательности
и
сходятся,
то сходится последовательность ![]() и
и
![]()
Доказательство. Пусть ![]() .
Тогда
.
Тогда ![]() и
и ![]() при
.
Поэтому
при
.
Поэтому
![]()
В силу свойств 3.3.1-3.3.3 бесконечно малых последовательностей
![]()
Свойство
3.4.3. Если
последовательности
и
сходятся
к
и ![]() соответственно,
то последовательность
соответственно,
то последовательность ![]() сходится
к
сходится
к ![]()
Доказательство. Так
как ![]() (пусть
для определенности
(пусть
для определенности ![]() ),
то по свойству
3.2.3,
начиная с некоторого номера
),
то по свойству
3.2.3,
начиная с некоторого номера ![]() .
Поэтому определена
последовательность
.
Поэтому определена
последовательность
![]() и
и ![]() Рассмотрим
для номеров
цепочку
равенств
Рассмотрим
для номеров
цепочку
равенств
![]()
Так
как последовательность ![]() --
бесконечно малая, а последовательность
--
бесконечно малая, а последовательность ![]() ограничена,
то
ограничена,
то 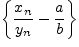 --
бесконечно малая последовательность,
следовательно, по свойству
3.3.3,
последовательность
--
бесконечно малая последовательность,
следовательно, по свойству
3.3.3,
последовательность ![]() стремится
к
стремится
к ![]() .
.
Теорема Кантора о вложенных отрезках
Теорема
(Г.Кантора). Пусть
задана система вложенных отрезков ![]() на
на ![]() ,
т. е. таких, что
,
т. е. таких, что
![]()
и
длины отрезков ![]() при
.
Тогда существует, и притом единственная,
точка, одновременно принадлежащая всем
отрезкам
при
.
Тогда существует, и притом единственная,
точка, одновременно принадлежащая всем
отрезкам ![]() .
.
Доказательство. Возьмем
любое ![]() .
Ясно, что для любого
.
Ясно, что для любого ![]() (из
вложенности системы отрезков, см.
рис. 4.1.1)
(из
вложенности системы отрезков, см.
рис. 4.1.1)
![]()

Рис. 4.1.1
Рассмотрим
последовательность левых концов отрезков
системы ![]() .
Она монотонно возрастает и ограничена
сверху, например, числом
.
Она монотонно возрастает и ограничена
сверху, например, числом ![]() .
Тогда, по основной теореме
2.4.1,
существует число (точка)
.
Тогда, по основной теореме
2.4.1,
существует число (точка) ![]() такое,
что
такое,
что ![]() и
для любого
и
для любого ![]() .
В частности, при
.
В частности, при![]() ,
что означает, что
,
что означает, что ![]() .
Так как
было
взято произвольным, то точка
.
Так как
было
взято произвольным, то точка ![]() принадлежит
всем отрезкам
принадлежит
всем отрезкам ![]() .
.
Найденная
точка единственная, так как, если
существует ![]() и
для любого
и
для любого ![]() ,
то для любого
выполняются
неравенства
,
то для любого
выполняются
неравенства![]() ,
что противоречит тому, что
,
что противоречит тому, что ![]() при
.
при
.
Замечание
4.1.1. ![]() ,
т.е. последовательность
левых
концов отрезков
,
т.е. последовательность
левых
концов отрезков ![]() ,
возрастая, стремится к точке
,
а последовательность
,
возрастая, стремится к точке
,
а последовательность ![]() правых
концов отрезков
,
убывая, стремится к
.
Действительно,
правых
концов отрезков
,
убывая, стремится к
.
Действительно,
![]()
Замечание
4.1.2. Во
множестве рациональных чисел ![]() такого
свойства, вообще говоря, нет. Например,
пусть
такого
свойства, вообще говоря, нет. Например,
пусть ![]() ,
а
,
а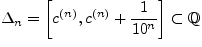 .
Ясно, что эта последовательность отрезков
удовлетворяет условиям теоремы Кантора,
но общая единственная точка
.
Ясно, что эта последовательность отрезков
удовлетворяет условиям теоремы Кантора,
но общая единственная точка ![]() --
иррациональное число, следовательно,
во множестве рациональных чисел
общих
точек у рассматриваемой системы отрезков
нет, т. е.
--
иррациональное число, следовательно,
во множестве рациональных чисел
общих
точек у рассматриваемой системы отрезков
нет, т. е.
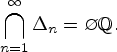
Замечание
4.1.3. То,
что в теореме Кантора речь идет о системе
отрезков (а, например, не интервалов),
существенно. Достаточно рассмотреть
систему интервалов 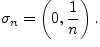 Ясно,
что
Ясно,
что ![]() в
в ![]()
Теорема Больцано-Вейерштрасса об ограниченных последовательностях.
Теорема
4.3.2 (Больцано - Вейерштрасса). Из
всякой ограниченной последовательности ![]() можно
выделить подпоследовательность,
сходящуюся к некоторому действительному
числу.
можно
выделить подпоследовательность,
сходящуюся к некоторому действительному
числу.
Доказательство (метод
Больцано). Так как последовательность ![]() ограничена,
то существует число
такое,
что
ограничена,
то существует число
такое,
что ![]() .
Разделим отрезок
.
Разделим отрезок ![]() на
два равных отрезка и обозначим
через
на
два равных отрезка и обозначим
через ![]() какой-нибудь
из них, содержащий бесконечно много
элементов из
,
пусть
какой-нибудь
из них, содержащий бесконечно много
элементов из
,
пусть ![]() .
Далее разделим отрезок
на
два равных отрезка и обозначим
через
.
Далее разделим отрезок
на
два равных отрезка и обозначим
через ![]() какой-нибудь
из них, содержащий бесконечно много
элементов из
.
Тогда найдется элемент
какой-нибудь
из них, содержащий бесконечно много
элементов из
.
Тогда найдется элемент ![]() и
и ![]() .
Процесс деления отрезка пополам, выбора
одной из половин отрезка и элемента в
ней продолжим по индукции. Итак, построена
система вложенных отрезков
.
Процесс деления отрезка пополам, выбора
одной из половин отрезка и элемента в
ней продолжим по индукции. Итак, построена
система вложенных отрезков ![]() и
последовательность
и
последовательность![]() такая,
что для любого
такая,
что для любого ![]() выполняется
выполняется ![]() и
и ![]() .
Тогда по теореме Кантора о вложенных
отрезках существует единственная
точка
,
принадлежащая всем отрезкам, и
.
Тогда по теореме Кантора о вложенных
отрезках существует единственная
точка
,
принадлежащая всем отрезкам, и ![]() .
Переходя к пределу по
.
Переходя к пределу по ![]() в
неравенствах
в
неравенствах ![]() ,
получим
,
получим ![]() .
.
