
- •Единственность предела сходящейся последовательности
- •Ограниченность сходящейся последовательности
- •Свойства бесконечно малых последовательностей.
- •Арифметические свойства сходящихся последовательностей.
- •Теорема Кантора о вложенных отрезках
- •Теорема Больцано-Вейерштрасса об ограниченных последовательностях.
- •Критерий Коши сходимости последовательности.
- •*Теорема о существовании точных границ числовых множеств.
- •*Принцип Бореля-Лебега
- •*Теорема Больцано-Вейерштрасса о существовании предельной точки у ограниченного числового множества
- •Эквивалентность 2х определений предела функции в точке
- •*Критерий Коши предела функции в точке
- •Непрерывность сложной функции
- •Теоремы Вейерштрасса для непрерывных функций на отрезке
- •Теорема Больцано-Коши о нулях функции
- •*Теорема о существовании обратной функции
- •*Теорема о существовании и непрерывности обратной функции
- •Непрерывность дифференцируемой функции
- •Доказательство
- •Производная и дифференцируемость функции в точке
- •Дифференцируемость функции в точке: правила дифференцирования, дифференцируемость сложной функции
- •Правила дифференцирования
- •25. Теоремы о среднем: Ферма, Ролля, Лагранжа, Коши Теоремы Ферма и Ролля.
- •Теоремы Коши и Лагранжа.
- •26. Правила Лопиталя
- •27. *Теорема Тейлора
- •28. Достаточные условия экстремума
- •29. Точки возрастания функции и второе достаточное условия экстремума функции в точке
*Теорема Больцано-Вейерштрасса о существовании предельной точки у ограниченного числового множества
Всякое бесконечное ограниченное числовое множество имеет, по крайней мере, одну предельную точку.
Доказательство. Пусть X - бесконечное ограниченное множество чисел из R. Из определения ограниченности множества X следует, что X содержится в некотором отрезке [a, b]. Обозначим отрезок [a, b] через σ0 и покажем, что существует, по крайней мере, одна точка x0 ∈ [a, b], которая является предельной для X. Разделим отрезок σ0 на два равных отрезка и обозначим через σ1 = [a1, b1] любой из них, содержащий бесконечное подмножество чисел множества X (по крайней мере, один из них обязательно содержит такое бесконечное подмножество). Теперь σ1 разделим на два равных отрезка и обозначим через σ2 = [a2, b2] любой из них, содержащий бесконечное подмножество чисел множества X.
Рассуждая по индукции, получим последовательность вложенных друг в друга отрезков σn = [an, bn] (n = 0, 1, 2, . . . ), длины которых (b – a)/2n стремятся к нулю.
Согласно принципу Кантора о вложенных отрезках существует точка x0, принадлежащая всем σn. Очевидно, что x0 есть предельная точка множества X.
Эквивалентность 2х определений предела функции в точке
Определение
предела функции по Гейне. Пусть
в каждой точке интервала ![]() ,
кроме, быть может, точки
,
кроме, быть может, точки ![]() ,
определена функция
,
определена функция ![]()
Число ![]() называется пределом функции
при
стремлении
называется пределом функции
при
стремлении ![]() к
к ![]() ,
если для любой последовательности
такой,
что
,
если для любой последовательности
такой,
что
![]()
последовательность ![]() значений
функции
сходится
к
при
.
В этом случае пишут
значений
функции
сходится
к
при
.
В этом случае пишут
![]()
Определение
предела функции по Коши. Пусть
в каждой точке интервала
,
кроме, быть может, точки
,
определена функция
(см.
рис. 5.2.2). Число
называется пределом функции
при
стремлении
к
,
если для любого
существует ![]() такое,
что для всех
такое,
что для всех![]() ,
удовлетворяющих условию
,
удовлетворяющих условию ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() .
Или, на формальном языке,
.
Или, на формальном языке,
![]()
Определения предела функции по Гейне и по Коши эквивалентны
![]()
Доказательство.
Необходимость. Докажем
от противного. Пусть ![]() по
Гейне, но не по Коши, т. е.
по
Гейне, но не по Коши, т. е.
![]()
![]()
Пусть ![]() .
Тогда по (5.2.2) найдутся
.
Тогда по (5.2.2) найдутся ![]()
![]() и
и ![]() .
Отсюда
.
Отсюда ![]() ,
и по билет
5
,
и по билет
5 ![]() .
Поэтому, по определению Гейне,
.
Поэтому, по определению Гейне, ![]() ,
но по построению последовательность
,
но по построению последовательность ![]() лежит
вне окрестности
лежит
вне окрестности ![]() ,
что противоречит тому, что
.
,
что противоречит тому, что
.
Достаточность. Пусть
![]() (по
Коши).
(по
Коши).
Согласно
определению Гейне, возьмем любую
последовательность ![]() .
Для доказательства того, что
,
возьмем любое
.
Тогда из определения предела по Коши
найдется соответствующее
.
Для доказательства того, что
,
возьмем любое
.
Тогда из определения предела по Коши
найдется соответствующее ![]() .
Для
,
в силу сходимости
,
найдется номер
такой,
что для всех
.
Для
,
в силу сходимости
,
найдется номер
такой,
что для всех ![]() ,
но тогда по определению Коши
,
но тогда по определению Коши ![]() ,
что доказывает, что
,
т. е.
,
что доказывает, что
,
т. е. ![]() (по
Гейне).
(по
Гейне).
*Критерий Коши предела функции в точке
Говорят, что функция удовлетворяет условию Коши в точке , если она определена в , быть может, кроме самой точки , и выполнено
![]()
![]()
Теорема
5.3.1. Для
того чтобы существовал конечный
предел ![]() необходимо
и достаточно, чтобы в точке
выполнялось
условие Коши для функции
необходимо
и достаточно, чтобы в точке
выполнялось
условие Коши для функции ![]()
Доказательство.
Необходимость.
легко следует из определения предела
по Коши .Действительно, возьмем любое
,
тогда для ![]() найдется
найдется![]() .
Возьмем любые
.
Возьмем любые ![]() ,
тогда
,
тогда
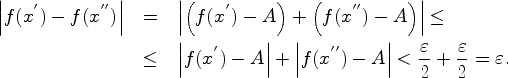
Достаточность. Пусть выполняется условие . Докажем, что существует
![]() (по
Гейне).
(по
Гейне).
Пусть
дана любая последовательность ![]() Возьмем
любое
,
по нему найдем
,
тогда существует номер
такой,
что для всех
Возьмем
любое
,
по нему найдем
,
тогда существует номер
такой,
что для всех ![]() ,
а следовательно, выполняется неравенство
,
а следовательно, выполняется неравенство ![]() .
Отсюда
фундаментальна,
значит, последовательность
сходится
к некоторому числу
.
Отсюда
фундаментальна,
значит, последовательность
сходится
к некоторому числу ![]() .
Остается доказать, что и для другой
последовательности
.
Остается доказать, что и для другой
последовательности ![]() .
Действительно, по изложенному выше
существует
.
Действительно, по изложенному выше
существует ![]() при
.
Рассмотрев третью последовательность
при
.
Рассмотрев третью последовательность
![]()
будем
иметь ![]() .
Следовательно,
.
Следовательно,
![]()
