10. Точки разрыва функций.

Ф-ия явл-ся непрерывной, если lim_xxof(x)=f(х_о) <=> lim_xxo-0f(x)= lim_xxo+0f(x)=f(x).

Опре.1. Точки в к-ых наруш-ся условие непрерывности наз-ся точками разрыва.

О пре.2. Т.разрыва наз-ся т.разрыва I рода, если сущ-ют конеч односторон пределы в этой точке.

Опре.3. Т.разрыва I рода наз-ся т.устранимого разрыва, если односторон пределы в этой точке равны.

Опре.4. Скачком ф-ии в т.разрыва I рода наз-ся модулем разности однострон пределов в этой точке.

Опре.5.Т. х_о наз-ся т. Разрыва II рода, если хотя бы один из 2-х односторон пределов=±∞. Примеры: 1.f(x)=(x²–9)/(x–3), x=3 – т.разрыва I рода; lim_xa((x²-9)/(x-3))=lim_xa(x+3)=6 ±∞ II рода.

11. Производня функция.

Пусть ф-ия у=f(x) b определена и непрерыв на (a,b), пусть х_о (a,b). Дадим в точке х_о приращение аргументы х так, что точка х_о+х(a,b). Тогда ф-ия получ соответствующее приращение у=f(х_о+х)-f(х_о). Опред1. Производной ф-ии в данной точке наз-ся предел отношения приращения ф-ии к приращению аргумента, когда приращение аргумента стремится к 0, если этот предел сущ-ет и конечен. Ф-ия наз-ся дифференцируемой в точке х_о. lim_х0у/х=f( х_о).

Опре2. Ф-ия наз-ся дифференцируемой на множестве А  R, если она диф-ма в каждой точке множества А.

12. Геометрический смысл производной.

П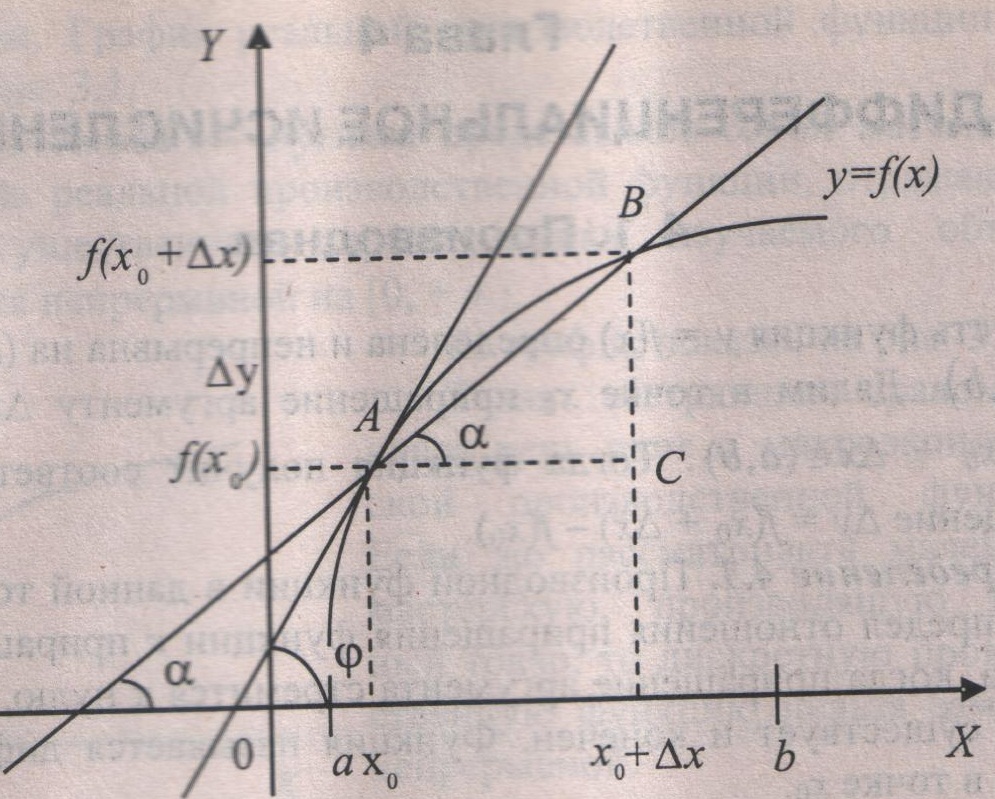 роизводной ф-ии в данной точке наз-ся предел отношения приращения ф-ии к приращению аргумента, когда приращение аргумента стремится к 0, если этот предел сущ-ет и конечен. Ф-ия наз-ся дифференцируемой в точке х_о. lim_х0у/х=f( х_о).

Опред. Касательной к плоской кривой наз-ся предельное положение секущей, когда 2-ая точка пересечения неограниченно приближается по кривой к первой точки. Пусть ф-ия у=f(x) определена и непрерывна на (a,b) и т. х_о (a,b). Дадим т. х_о приращение х_о+х(a,b) тогда ф-ия получит приращение у=f(х_о+х)-f(х_о) Проведем касат к гр ф-ии через т.А. Рассмотрим АВС: tg=BC/AC=y/x. При х0 ВА, секущая стремится к касательной, , tgtg, y/xf(x_o). Переходя к lim _х0у/х=f(x_o) получим tg=f(x_o). Таким образом, производная ф-ия в т. = tg угла наклона касательной, проведенной к графику в данной т-ке.

13. Связь между непрерывностью и дифференцируемостью функции.

Теор1 (необх условия диф-ти ф-ии). Если ф-ии диф-ема в т., то она непрерывна в этой точке.

Док-во: Пусть ф-ия у=f(x) диф-ема в т. x_о. Дадим т. х_о приращение х, тогда ф-ия получит приращение у. Найдем предел: lim_х0у = lim_х0(у*х)/х = lim_х0у/х* *lim_х0х=f(x_o)*0=0. lim_х0у=0, те ф-ия непрерывна (малому приращению аргумента х=0 соответ малое приращение ф-ии у=0). Следствие: если х_о – это т.разрыва ф-ии, то в ней ф-ия не диф-ема.

14. Свойства производных

Производной ф-ии в данной точке наз-ся предел отношения приращения ф-ии к приращению аргумента, когда приращение аргумента стремится к 0, если этот предел сущ-ет и конечен. Ф-ия наз-ся дифференцируемой в точке х_о. lim_х0у/х=f( х_о).

Теор1.производная пост-ой рана 0. (С=0)

Теор2. Производ алгеброич суммы конечного числа ф-ий = алгеброич сумме производ этих ф-ий.

Док-во: у=u+v-z u=u(x), v=v(x), z=z(x), y=y(x).

1). Дадим аргументу х приращ х, тогда ф-ия получ свое приращение uu, vv, zz, yy.

Получ равенство: y+y=(u+u)+(v+v)-(z-z).

2). Найдем у: y=u+u+v+v-z-z-u-v+z=u+v-z

3).Разделим все на х: у/x=u/x+v/x-z/x.

4). Переходим к lim_х0 слева и справа, получ:

lim_х0у/x=lim_х0u/x+lim_х0v/x-lim_х0z/x y=u+v-z чтд.

Теор3. Произв произведение 2-х диф-емых ф-ий равна (uv)=uv+uv. Док-во: пусть y=uv, u=u(x) v=v(x).

1). Дадим хх(х+х), uu(u+u), vv(v+v), yy(y+y): y+y=(u+u)(v+v).

2).Найдему: y= (u+u)(v+v)-uv= uv+vu+vu+uv-uv= uv-uv+ +uv

3). Делим все на х: у/x= uv/x-uv/x+uv/x.

4). Следствие. Пост множ-ь можно выносить за знак производной, (сu)=cu c-const.

Теор4. Производ частного 2-х ф-ий равна (u/v)=(uv-uv)/v²