1. Основные понятия теории вероятностей: событие; элементарный исход; пространство элементарных исходов; достоверное событие; невозможное событие; случайное событие; тождественные события; операции над событиями; событие, противоположное событию А; несовместные события; полная группа событий.

Событие - результат некоторого опыта или наблюдения.

Элементарный исход - элементарное неразложимое событие.

Пространство элементарных исходов - совокупность всех элементарных исходов в данном опыте.

Достоверное событие - событие, которое обязательно произойдет в данном опыте.

Невозможное событие - такое событие, которое в данном опыте произойти не может.

Случайное событие - событие, которое при осуществлении некоторой совокупности условий может произойти или не произойти

А=В : два события тождественны друг другу тогда и только тогда, когда эти события состоят из одних и тех же элементарных исходов.

А*В - произведение событий - событие, состоящее в наступлении обоих событий А и В

А+В - сумма событий - событие, состоящее в наступлении хотя бы одного из событий А или В.

А - В - разность событий - событие, состоящее в том, что событие А происходит, а событие В не происходит

А -событие, противоположное событию А - если событие А не происходит.

А+А = 

Несовместные события - события, одновременное появление которых невозможно.

А*В=

События В₁, В₂,…В_n образуют полную группу событий, если хотябы одно из них обязательно произойдет в результате опята.

В₁+В₂+…+В_n=

Примеры событий, образующих полную группу:

1. Выпадение герба иди решки при одном бросании монеты.

2. Попадание или промах при одном выстреле.

3. Появление 1,2,3,4,5 или 6 очков при одном бросании игральной кости.

4. Ни одного отказа, один отказ, 2 отказа или более двух отказов технического устройства за сутки.

5. Аналогично с опечатками.

2. Аксиоматика теории вероятностей. Классическое определение вероятности.

Аксиоматика теории вероятностей:

1. Аксиома существования вероятности: Каждому случайному событию А поставлено в соответствие неотрицательное число p(A) , называемое его вероятностью.

2. Вероятность достоверного события: Вероятность достоверного события =1.

3. Аксиома сложения: Если события А и В несовместны, то вероятность их суммы равна сумме их вероятностей. p(A+B)=p(A)+p(B)

4. Расширенная аксиома сложения: Если событие А равносильно наступлению хотябы одного из попарно несовместных событий А₁, А₂,…А_n,, т.е. событие А есть сумма событий А₁, А₂,…А_n:

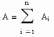
то вероятность события А равна сумме вероятностей событий А₁, А₂,…А_n:

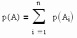
Следствие 1 (Вероятность противоположного события)

p(А)=1-p(A)

Следствие 2: (Вероятность невозможного события)

p()=0

Следствие 3: (Вероятность любого события)

p(A)[0;1]

Классическое определение вероятности.

Классическое определение вероятности основано на равновозможности или равновероятности элементарных исходов в некотором опыте.

Элементарные исходы являются равновозможными, если нет основания полагать , что какой-либо исход более возможен, чем другой. В общем случае рассмотрим полную группу, состоящую из конечного числа элементарных равновозможных несовместных исходов опыта.

Классическое определение вероятности формулируется так:

Вероятность события А равна отношению числа элементарных исходов, благоприятствующих событию, А(_m) к общему числу всех равновозможных несовместных элементарных исходов испытания, образующих полную группу (n)

р(А)=m/n, m- число общих исходов, благоприятствующих событию А.

3. Теорема сложения.

Для произвольных событий А и В верно:

p(A+B)=p(A)+p(B)-p(A*B)

Доказательство:

Представим событие А+В как сумму двух несовместных событий:

А+В=А+(В-А*В)

Тогда в силу аксиомы сложения имеем:

р(А+В)=р(А)+р(В-А*В)

Аналогично р(В)=р(А*В+[В-А*В])= р(А*В)+р(В-А*В)

р(В-А*В)=р(В)-р(А*В)  р(А+В)=р(А)+р(В-А*В):

р(А+В)=р(А)+ р(В)-р(А*В)

Что и требовалось доказать.

Теорему сложения можно обобщить на случай 3х событий:

р(А+В+С)=р(А)+ р(В) + р(С) -р(А*В) -р(А*С) -р(В*С)+р(А*В*С)

4. Условная вероятность. Теорема умножения вероятностей. Независимые события. Теорема умножения для независимых событий. Вероятность появления хотя бы одного события.

Условные вероятности.

Вероятность события А, вычисленная в предположении, что событие В уже произошло, называется условной вероятностью события А при условии В - Р_В(А)

Теорема умножения вероятностей

Вероятность произведения двух событий равна произведению вероятностей одного из событий на условную вероятность другого в предположении, что первое уже произошло.

Р(А*В)=Р(А)*Р_А(В)=Р(В)*Р_В(А)

Доказательство:

Пусть из общего числа элементарных исходов испытания n наступлению события А благоприятствует m исходов, а наступлению события В - k исходов из числа m исходов, благоприятствующих наступлению события А . Это значит, что совместному наступлению событий А и В благоприятствует k исходов из общего числа n.

P(A*B)=k/n=(k*m)/(n*m)=(m/n)*(k/m)

Первый множитель (m/n) представляет собой вероятность события А, Р(А). Второй множитель (k/m)- вероятность события В при условии, что В произошло, Р_А(В).

Если события А и В независимы, то условная вероятность = безусловной вероятности.

Р_А(В)= Р_В(А) =Р(А), тогда для независимых событий Р(А*В)=Р(А)*Р(В)

Вероятность появления хотя бы одного события

Теорема. Вероятность появления хотя бы одного из событий А1,А2,..Аn независимых в совокупности равна разности между единицей и произведением вероятностей противоположных событий

p(A)=1-q1q2.. q_n

q_i =1- p_i

Доказательство: А-появление хотя бы одного из событий

А1,А2,..Аn – ни одно из событий не допустимо. Являются противоположными.

p(A)=1-p(А1,А2,..Аn)=1- p(А1)p(А2)..p(Аn)=1- q1q2.. q_n

Для равновероятных событий А1,А2,..Аn

p(A)=1-q^n

5. Формула полной вероятности. Вероятность гипотез. Формулы Байеса.

Формула полной вероятности.

Пусть требуется определить вероятность некоторого события А, которое может произойти только вместе с одним из событий В₁, В₂,…В_n, образующих полную группу несовместных событий. Эти события называются гипотезами.

Вероятность события А вычисляется как сумма произведения вероятностей каждой гипотезына соответствующие условные вероятности

события А.

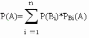
Доказательство:

Т.к. гипотезы В₁, В₂,…В_n образуют полную группу, то событие А может появиться только в комбинации с какой-либо из этих гипотез.

А=В₁*А+В₂*А+…+В_n*А

Так как гипотезы В₁, В₂,…В_n несовместны, то и события В₁*А, В₂*А, …В_n*А тоже несовместны. Тогда по теореме сложения:

Р(А)=р(В₁*А)+р(В₂*А)+…+р(В_n*А)=

/по теореме умножения/=Р(В₁)*Р_В1(А)+Р(В₂)*Р_В2(А)+…+ Р(В_n)*Р _Вn(А)=

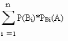
Формулы Байеса.

Следствием теоремы умножения и формулы полной вероятности является формула Байеса.

Пусть имеется полная группа несовместных событий - гипотез.

Вероятности этих гипотез до проведения опыта известны и равны соответственно Р(В₁), Р(В₂),..Р(В_n). Эти вероятности называются априорными.

Произведен опыт, в результате которого произошло некоторое событие А.. Требуется пересчитать вероятности гипотез в связи с появлением этого события, т.е. вычислить условную вероятность. Р_А(В_i) для каждой гипотезы.

Условные вероятности гипотез после проведения опыта реализации события А называются апостериорными.

По теореме умножения:

Р(А*В_i)=Р(А)*Р_А(В_i)=Р(В_i)*Р_Bi(А)Р_A(В_i)= Р(В_i)*Р_Bi(А)

Р(А)

6. Случайная величина: определение, виды случайных величин, способы задания. Функция распределения вероятностей случайной величины (определение и свойства).

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, заранее не известное и зависящее от случайных причин, которые не могут быть учтены.

Дискретные случайные величины – это случайные величины, которые могут принимать только конечное или счетное множество значений.

Непрерывные случайные величины – это случайные величины, возможные значения которых образуют некоторый конечный или бесконечный интервал.

Любое правило (таблица, функция, график), позволяющее находить вероятности отдельных значений случайной величины или множества этих значений, называется законом распределения случайной величины (или просто распределением).

Для дискретной случайной величины закон распределения может быть задан в виде таблицы распределения. Такую таблицу называют рядом распределения. Закон распределения дискретной случайной величины можно задать графически многоугольником распреденления.

Функцией распределения вероятностей случайной величины Х называют вероятность того, что эта случайная величина примет значение, меньшее, чем х:

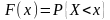
Свойства функции распределения:

Значения функции распределения принадлежат отрезку [0,1]:

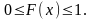
F(x) – неубывающая функция, то есть 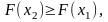если .

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале [a,b), равна приращению функции распределения на этом интервале:

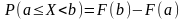
Следствие 2. Вероятность того, что непрерывная случайная величина примет одно определенное значение, равна нулю.

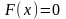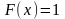3. Если возможные значения случайной величины принадлежат интервалу (a,b), то при и при .

Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси x, то справедливы следующие предельные соотношения:

7. Плотность распределения непрерывной случайной величины (определение и свойства). Отыскание функции распределения непрерывной случайной величины по известной плотности распределения.

Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(x) – первую производную от функции распределения F(x): .

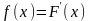Из этого определения следует, что функция распределения является первообразной для плотности распределения.

Свойства плотности распределения:

Плотность распределения является неотрицательной функцией: 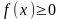для любого x. Это свойство следует из того, что функция распределения F(x) – неубывающая функция.

Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b:

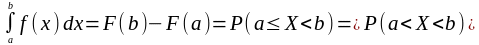. (6)

Геометрически это можно истолковать так: вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b), равна площади криволинейной трапеции, ограниченной осью Ox, кривой распределения f(x) и прямыми x = a и x = b (см. рис.1).

Следствие 1. Несобственный интеграл от плотности распределения в пределах от 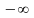до 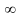равен единице:

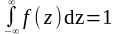(7)

Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ox и кривой распределения, равна единице.

Следствие 2. Зная плотность распределения f(x), можно найти функцию распределения F(x) по формуле:

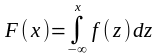. (8)