- •6. Случайная величина: определение, виды случайных величин, способы задания. Функция распределения вероятностей случайной величины (определение и свойства).
- •7. Плотность распределения непрерывной случайной величины (определение и свойства). Отыскание функции распределения непрерывной случайной величины по известной плотности распределения.
- •8. Математическое ожидание случайной величины (определение и свойства).
- •9. Отклонение случайной величины (определение и свойства).
- •10. Дисперсия случайной величины (определение и свойства). Среднеквадратическое отклонение случайной величины (определение и свойства).
- •11. Распределение Бернулли (определение, закон распределения, функция распределения, график функции распределения, числовые характеристики).
- •12. Геометрическое распределение (определение, закон распределения, функция распределения, график функции распределения, числовые характеристики).
- •13. Биномиальное распределение (определение, закон распределения, график функции распределения, числовые характеристики).
- •14. Распределение Пуассона (определение, закон распределения (с выводом), функция распределения, график функции распределения, числовые характеристики).
- •16. Показательное (экспоненциальное) распределение (определение, плотность распределения, функция распределения, графики плотности и функции распределения, числовые характеристики).
- •20. Условные функция и плотность распределения. Зависимые и независимые случайные величины.
- •21. Числовые характеристики зависимости (ковариация, коэффициент корреляции – определение и свойства). Ковариационная матрица. Некоррелированные случайные величины.
- •22. Двумерное нормальное распределение. Вероятность попадания в эллипс равной вероятности.
- •23. Предельные теоремы теории вероятностей.
- •Неравенство Чебышева
- •Теорема Бернулли
- •Теорема Ляпунова
- •25. Цепь Маркова. Матрица вероятностей переходов. Однородная цепь Маркова. Предельные вероятности состояний. Марковский процесс с дискретными состояниями и непрерывным временем.
- •26. Генеральная и выборочная совокупности. Повторная и бесповторная выборки. Репрезентативная выборка. Способы отбора.
- •27. Статистическое распределение выборки. Полигон и гистограмма. Эмпирическая функция распределения и её свойства.
- •28. Несмещенные, эффективные и состоятельные оценки. Генеральная и выборочная средние.
- •29. Генеральная и выборочная дисперсии. Формула для вычисления дисперсии. Оценка генеральной дисперсии по исправленной выборочной.
20. Условные функция и плотность распределения. Зависимые и независимые случайные величины.
Условным законом распределения одной из случайных величин, входящих в систему (X,Y), называется её закон распределения, найденный при условии, что другая случайная величина приняла определённое значение (или попала в какой-то интервал).
Пусть (X,Y) – дискретная двумерная случайная величина и
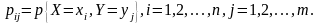
Условной плотностью распределения составляющей X при условии Y=y называют отношение плотности совместного распределения к плотности распределения составляющей Y:
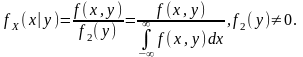
Случайные величины X и Y называются независимыми, если события {X<x} и {Y<y} независимы при любых x и y. В противном случае величины называются зависимыми.
Теорема. Для того, чтобы случайные величины X и Y были независимы, необходимо и достаточно, чтобы функция распределения системы (X,Y) была равна произведению функций распределения составляющих:
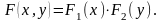
Необходимым и достаточным условием взаимной независимости n случайных величин является равенство:

для n непрерывных случайных величин
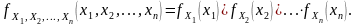
21. Числовые характеристики зависимости (ковариация, коэффициент корреляции – определение и свойства). Ковариационная матрица. Некоррелированные случайные величины.
Ковариация случайных величин X и Y – это математическое ожидание произведения центрированных величин
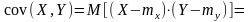
=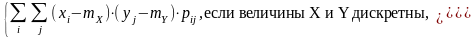
Теорема. Если случайные величины X и Y независимы, то
cov(X,Y)=0.
Коэффициентом корреляции случайных величин X и Y называют их нормированную ковариацию:
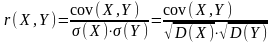 .
.
Теорема. Если случайные величины X и Y связаны линейной зависимостью Y=aX+b, то коэффициент корреляции:

Ковариационная матрица случайного вектора (X1, X2, … , Xn) – это матрица, состоящая из элементов
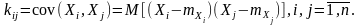
Если
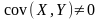 ,
то случайные величины X
и Y зависимы. В этом случае
(
)
их называют коррелированными.
Однако из того, что
,
то случайные величины X
и Y зависимы. В этом случае
(
)
их называют коррелированными.
Однако из того, что
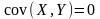 ,
не следует независимость X
и Y. В этом случае (
)
случайные величины называют
некоррелированными. Из
независимости вытекает некоррелированность;
обратное, вообще говоря, неверно.
,
не следует независимость X
и Y. В этом случае (
)
случайные величины называют
некоррелированными. Из
независимости вытекает некоррелированность;
обратное, вообще говоря, неверно.
22. Двумерное нормальное распределение. Вероятность попадания в эллипс равной вероятности.
Плотность двумерной нормальной случайной величины (X,Y) имеет вид
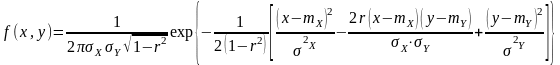
Здесь
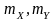 - математические ожидания величин X
и Y;
- математические ожидания величин X
и Y;
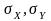 - средние квадратичные отклонения
величин X и Y;
r – коэффициент корреляции
величин X и Y.
- средние квадратичные отклонения
величин X и Y;
r – коэффициент корреляции
величин X и Y.
Теорема: из некоррелированности нормально распределенных случайных величин следует их независимость.
Плотность распределения нормального закона системы случайных величин сохраняет постоянное значение на эллипсах:
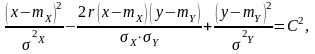
где С – постоянная; на этом основании такие эллипсы носят название эллипсов равных вероятностей. Можно показать, что вероятность попадания точки (X,Y) внутрь эллипса равной вероятности равна