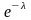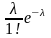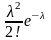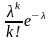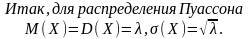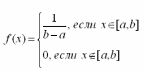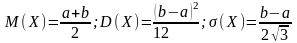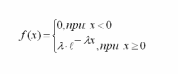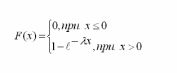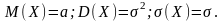14. Распределение Пуассона (определение, закон распределения (с выводом), функция распределения, график функции распределения, числовые характеристики).

Дискретная случайная величина Х имеет распределение Пуассона, если её возможные значения равны 0, 1, 2, … , k, … , а соответствующие вероятности выражаются формулой Пуассона

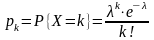. (22)

Распределение Пуассона является предельным для биномиального распределения, когда 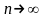и 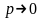так, что 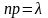- постоянно.

Теорема Пуассона. Если в схеме Бернулли ; так, что , то 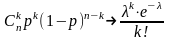при любых k, k = 0, 1, 2, …

Случайная величина Х, распределённая по закону Пуассона, имеет следующий ряд распределения:

Х	0	1	2	…	k	…
р				…		…

15. Равномерное распределение (определение, плотность распределения, функция распределения, графики плотности и функции распределения, числовые характеристики).

Понятие равномерного распределения соответствует представлению о выборе точки из определенного отрезка наудачу.

Случайная величина X распределена равномерно на отрезке [a,b], если ее плотность постоянна и равна

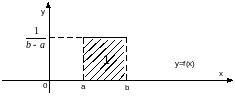
Найдём функцию распределения вероятностей:

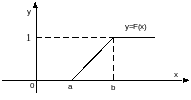
16. Показательное (экспоненциальное) распределение (определение, плотность распределения, функция распределения, графики плотности и функции распределения, числовые характеристики).

Экспоненциально распределенной называется такая случайная величина, для которой плотность вероятности имеет вид

Здесь 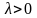- параметр распределения.

Функция распределения вероятностей показательного распределения имеет вид

(34)

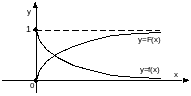
Найдём вероятность попадания случайной величины Х, распределённой по показательному закону, в интервал (a,b). Используя формулы (3) и (34), получаем

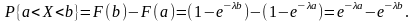
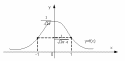
17. Нормальное распределение (плотность распределения, свойства плотности распределения, её график, влияние параметров распределения на форму нормальной кривой, стандартное нормальное распределение, числовые характеристики). Вероятность попадания нормально распределенной случайной величины в заданный интервал. Правило трёх сигм.

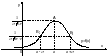
При изменении параметра a форма кривой сохраняется, но она перемещается вдоль оси Oх - вправо при возрастании a и влево при убывании a. С увеличением 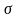кривая будем снижаться и вытягиваться вдоль оси Ох.

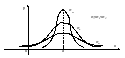
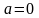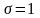Если и , то 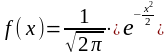и нормальное распределение называется нормированным или стандартным.

Вероятность попадания нормально распределённой случайной величины в заданный интервал

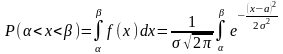
Правило трёх сигм

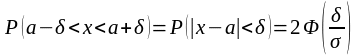
Положив в 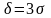, получим:

.

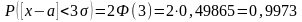18. Система случайных величин: определение, виды, способы задания. Функция распределения двумерной случайной величины (определение, геометрическая интерпретация, свойства). Вероятность попадания случайной точки в полуполосу, в прямоугольник.

Случайным вектором (n-мерной случайной величиной, системой n случайных величин) называют упорядоченный набор из n случайных величин (Х₁, Х₂, … , Х_n).

Системы случайных величин могут быть дискретными, непрерывными и смешанными.

Функцией распределения двумерной случайной величины (X,Y) называют вероятность совместного выполнения двух неравенств {X<x} и {Y<y}: .

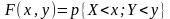Геометрическая интерпретация: если двумерную случайную величину (X,Y) рассматривать как случайную точку в прямоугольной декартовой системе координат, то функция распределения F(x,y) есть вероятность попадания случайной точки (X,Y) в бесконечный квадрант с вершиной в точке (x,y), лежащий левее и ниже её.

Свойства функции распределения двумерной случайной величины

, так как это вероятность.

F(x,y) есть неубывающая функция своих аргументов, то есть

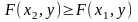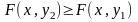при _,

при _.

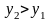Если хотя бы один из аргументов обращается в -∞, то функция распределения F(x,y) равна нулю: .

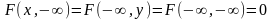Если оба аргумента равны +∞, то функция распределения F(x,y) равна единице: .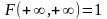

При одном из аргументов, равном +∞, функция распределения двумерного вектора превращается в функцию распределения компоненты, соответствующей другому аргументу: .

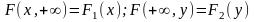Вероятность попадания случайной точки в полуполосу

p{X<x, y₁<Y<y₂} = F(x,y₂) - F(x,y₁).

Таким образом, вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов.

Вероятность попадания случайной точки в прямоугольник

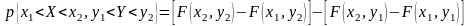
19. Плотность распределения двумерной непрерывной случайной величины (определение и свойства). Отыскание функции распределения двумерной непрерывной случайной величины по её плотности. Функция и плотность распределения n-мерной случайной величины

Плотностью распределения двумерной непрерывной случайной величины называют предел отношения вероятности попадания случайной величины в малый прямоугольник к площади этого прямоугольника, когда оба его размера стремятся к нулю:

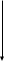
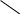y R_∆

∆y

∆x x

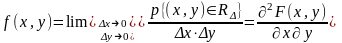
Плотность распределения двумерной непрерывной случайной величины вычисляется как вторая смешанная частная производная от функции распределения.

Свойства плотности распределения двумерной случайной величины

1) Плотность распределения двумерного случайного вектора есть функция неотрицательная:

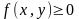
2) Вероятность попадания случайной точки (X,Y) в область D равна двойному интегралу от плотности по области D:

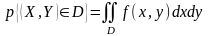
3) Функция распределения двумерной случайной величины выражается через плотность распределения следующим образом:

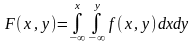
4) Условие нормировки: двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице:

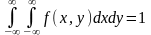
5) Плотности распределения компонент двумерного случайного вектора могут быть получены по формулам:

, .

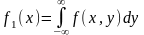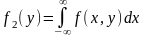Функция распределения n-мерной случайной величины - это вероятность совместного выполнения неравенств вида: {X_i<x_i}:

F(x₁, x₂, … , x_n) = p{ X₁<x₁; X₂<x₂; … ; X_n<x_n}.

Плотность распределения n-мерной случайной величины 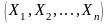– это n-ная смешанная частная производная функции распределения , взятая один раз по каждому аргументу: