Вопрос 20.

Свойства неопределенного интеграла.

∫c f(x) dx=c*∫ f(x) dx

∫(f(x) +g(x))dx=∫f(x)dx +∫g(x)dx

∫f`(x)dx=f(x)+C

(∫f(x)dx)`=f(x)

Табличные интегралы.

Смотреть в тетради.

Вопрос 21.

Замена переменной в неопределенном интеграле.

   ∫f(g(x))*g`(x)dx=∫f(g(x))dgx=∫f(t)dt ,где g(x)=t

Формула интегрирования по частям.

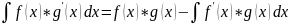
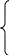∫ f(x)*dg(x)=f(x) *g(x)-∫g(x)*df(x)

sinkx arksinkx

Многочлен f(x) * coskx многочлен g`(x) * arktgkx

e^kx lnx

g`(x) f(x)

Вопрос 22.

22.1 Определенный интеграл, его геометрический смысл и свойства.

1) Определенным интегралом от функции f(x) по отрезку [a,b] называется предел интегральных сумм этой функции, когда мелкость разбиения отрезка [a,b] стремится к 0.

2) Определённый интеграл 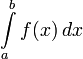  численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).

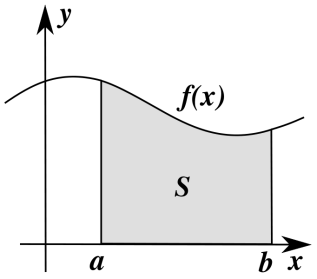
3) Свойства определенного интеграла.

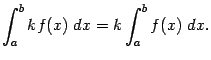
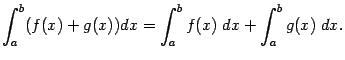
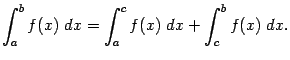
Формула Ньютона-Лейбница.

Если f(x) непрерывна на [a;b] и F(x) – некоторая её первообразная, то:

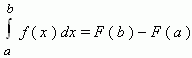
Вопрос 23.

Замена переменной в определенном интеграле

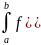
Интегрирование по частям

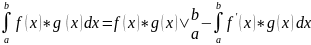
Запись 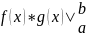означает выражение f(b)*g(b)-f(a)*g(a)

Вопрос 24.

Площадь криволинейной трапеции.

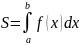
Пусть f(x)≥g(x) для любого х принадлежащего [a;b]. Тогда площадь фигуры ограниченной линиями y=f(x), y=g(x), x=a, x=b, равна:

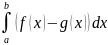
Объем тела вращения.

Объем тела, образованного вращением данной криволинейной трапеции находится по формуле:

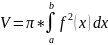
Вопрос 25.

Дифференциальные уравнения 1-го порядка.

Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида

F(x, y, y`) = 0 (1)

Решением дифференциального уравнения называется точная функция у=у(х), что при подстановке этой функции и её производных в дифференциальное уравнение получаем тождество.

Множество всех решений уравнения (1) называется его общим решением. Другими словами, общее решение дифференциального уравнения – это функция y = у (x, С), удовлетворяющая условиям:

1. При любом конкретном значении С=С₀, функция у(x, С) является решением данного диф.уравнения

2. Для любого решения данного диф.уравнения у=у*(х) существует значение С=С* такое, что у(х;С*)=у*(х)

График решения дифференциального уравнения называется интегральной прямой.

Задача Коши.

(1) y’=f(x, y) – дифференциальное уравнение 1-го порядка, разрешенное относительно производной.

Задача Коши состоит в том, чтобы найти решение дифференциального уравнения (1), удовлетворяющего начальному условию.

y(x₀)=y₀, где x₀,y₀ – заданные числа.

Начальное условие y(x₀)=y₀ означает, что интегральная кривая, соответствующая искомому решению, должна проходить через точку М (x₀,y₀).

Задача Коши состоит в том, чтобы найти интегральную кривую, проходящую через точку М, где x₀,y₀ – заданные числа.

Теорема Коши.

Пусть дано дифференциальное уравнение y’=f(x, y) причем функция f(x, y) определена в некоторой области D и f(x, y) и 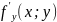непрерывны в этой области.

Тогда для любой точки (х₀;у₀) из области D существует решение задачи Коши

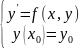причем единственное.

Если выполняется условие теоремы Коши, то через любую точку (х₀,у₀) области D можно провести ровно одну интегральную прямую.