- •Вопрос 2
- •Вопрос 3.
- •Вопрос 5.
- •Вопрос 6.
- •Вопрос 7.
- •Вопрос 8.
- •Вопрос 9.
- •Вопрос 10.
- •Вопрос 11.
- •Вопрос 12.
- •Вопрос 13.Большее значение функции) рвале, если доя любых точек х
- •Вопрос 14.
- •Вопрос 15.
- •Вопрос 16.
- •Вопрос 17.
- •Вопрос 18
- •Вопрос 19.
- •Вопрос 20.
- •Вопрос 21.
- •Вопрос 22.
- •Вопрос 23.
- •Вопрос 24.
- •Вопрос 25.
- •Вопрос 26.
- •Вопрос 27.
- •Вопрос 28.
- •Вопрос 29.
- •Вопрос 30. Несобственный интеграл по неограниченному промежутку.
Вопрос 26.
Дифференциальные уравнения 1-го порядка с разделяющимися переменными.
y`=f(x)*g(x),
y`/g(y)=f(x)
y`dx/g(y)=f(x)dx
dy/g(y)=f(x)dx
∫dy/g(y)=∫f(x)dx
f(x)=lnef(x)
Вопрос 27.
Линейные дифференциальные уравнения 2-го порядка.
1) Однородные:
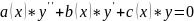 ,
(1)
,
(1)
где a(x), b(x), c(x) – функции зависящие от x.
2) Неоднородные:
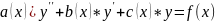 ,
(2)
,
(2)
Функции y1(x) и y2(x) называется линейно независимыми, если
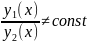
Теоремы об общем решении однородного и неоднородного уравнений.
1) Если y1(x) и y2(x) – два линейно независимых решения линейного однородного диф. уравнения 2-го порядка (1), то общее решение этого уравнения можно представить в виде:
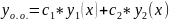 ,
,
то задача решения уравнения (1) сводится к нахождению двух его частных линейно независимых решений.
2)
Пусть
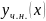 – некоторое частное решение уравнения
(2),
– некоторое частное решение уравнения
(2),
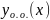 – общее решение соответствующего
однородного дифференциального уравнения.
Тогда общее решение диф. уравнения (2)
можно задать следующей формулой:
– общее решение соответствующего
однородного дифференциального уравнения.
Тогда общее решение диф. уравнения (2)
можно задать следующей формулой:
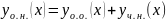
Вопрос 28.
Линейные диф. уравнения 2-го порядка с постоянными коэффициентами.
Уравнение вида
A y'' +By' +Cy = f(x),
где A,B,C – вещественные числа, f(x) – непрерывная функция, называется линейным дифференциальным уравнением с постоянными коэффициентами.
Нахождение общего решения однородного уравнения.
Рассмотрим линейное уравнение второго порядка вида:
y''+ρy'+qy=0, (1)
у которого правая часть f(x) равна нулю. Такое уравнение называется однородным.
Уравнение
K2+ρK+q=0 (2)
называется характеристическим уравнением данного уравнения (1).
Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через К1 и К2.
Общее решение уравнения (1) может быть записано в зависимости от величины дискриминанта D=b2–4ac уравнения (2) следующим образом:
При D>0 . Тогда уравнение (2) имеет два различных корня К1 и К2. Тогда получаем два решения дифференциального уравнения (1): y1=
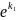 x
и y2=
x
и y2=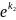 x
x
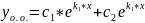
При D=0 корни характеристического уравнения равные К1=К2=К, и общее решение имеет вид:
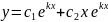
Если D<0, то корни характеристического уравнения комплексные:
![]() ,
где
,
где ![]() –
мнимая единица,
–
мнимая единица, ![]() и
общее решение (К1=α+βi, К2=α–βi,
β≠0), имеет вид
и
общее решение (К1=α+βi, К2=α–βi,
β≠0), имеет вид
y = с1eαxcosβx+C2eαxsinβx.
Вопрос 29.
Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Подбор частного решения неоднородного уравнения при специальном виде правой части.
Это уравнения вида:
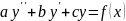
1. f(x) – многочлен степени n
A)
Если число «0» не является корнем харак.
уравнения, то
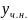 ищем
в виде многочлена степени n
ищем
в виде многочлена степени n
Б) Если число «0» является корнем харак. уравнения (кратности r), то уч.н. ищем в виде:
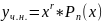 ,
где
,
где
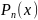 многочлен
степени n.
многочлен
степени n.
2.
f(x)
имеет вид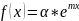
А) Если число m не является корнем харак. уравнения, то уч.н. ищем в виде
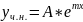
Б) Если число m не является корнем харак. уравнения (кратности r), то уч.н. ищем в таком виде:
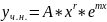
3.
Пусть
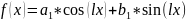
А) Если число li не является корнем харак. уравнения, то уч.н. ищем в таком виде:
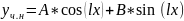
Б) Если число li является корнем характеристического уравнения (кратности r), то уч.н. ищем в таком виде: