
- •1.Матрицы и действия над ними. Умножение матриц.
- •4. Обратная матрица и ее вычисление.
- •5. Система линейных уравнений. Формулы Крамера.
- •6) Матричный метод решения системы уравнений. Метод Гаусса.
- •8. Скалярное произведение векторов и его свойства. Угол между двумя векторами в координатной форме. Условие ортогональности двух векторов.
- •9. Векторное произведение двух векторов, его свойства и геометрический смысл.
- •2. Свойства векторного произведения.
- •10. Смешанное произведение трех векторов и его геометрический смысл. Условие компланарности векторов.
- •4. Свойства смешанного произведения.
- •11. Параметрическое и каноническое уравнения прямой на плоскости.
- •16. Уравнения линий на плоскости. Кривые второго порядка: окружность и эллипс.
- •17. Гипербола и ее каноническое уравнение.
- •18. Парабола и ее каноническое уравнение.
- •19. Полярные координаты на плоскости. Связь между полярными и декартовыми координатами.
- •20. Функция. Способы задания функции. Основные характеристики функции.
- •Определение 1. Абсолютной величиной или модулем действительного числа называется само это число, если и число , если :
- •22. Числовая последовательность и ее предел. Сходимость числовой последовательности.
- •23. Предел функции в точке, предел функции в бесконечности. Бесконечно малые функции. Предел монотонных функций.
- •24. Первый замечательный предел.
- •25. Второй замечательный предел.
- •27. Точки разрывов, их классификация.
- •28. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.
- •29. Производная функции, ее геометрический и физический смысл. Связь между непрерывностью и дифференцируемостью функции.
- •30. Правила нахождения производной: производная произведения и производная частного.
- •32. Производные основных элементарных функций.
- •34. Логарифмическая производная.
- •35. Дифференцирование функций, заданных в параметрической форме. Неявная функция и ее производная.
- •36. Дифференциал функции, его свойства и геометрический смысл. Производные высших порядков.
- •37. Теорема Ферма и теорема Ролля.
- •38. Теорема Лагранжа и теорема Коши.
- •39. Правило Лопиталя раскрытия неопределенностей.
8. Скалярное произведение векторов и его свойства. Угол между двумя векторами в координатной форме. Условие ортогональности двух векторов.
Определение 3.14. Скалярным произведением векторов и называется число, равное произведению их длин на косинус угла между ними:
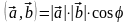 . (15)
. (15)
Свойства скалярного произведения.
Коммутативный закон:
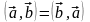 .
Действительно,
.
Действительно,
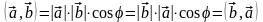 .
.Ассоциативный закон:
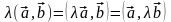 .
Действительно, например, при
:
.
Действительно, например, при
:
 .
Остальные случаи рассматриваются
аналогично.
.
Остальные случаи рассматриваются
аналогично.Дистрибутивный закон:
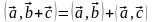 .
Действительно, используя формулу (15) и
свойства проекций, получаем:
.
Действительно, используя формулу (15) и
свойства проекций, получаем:
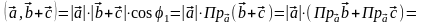
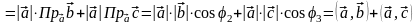 .
.Критерий перпендикулярности (ортогональности) Для того, чтобы два вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю.
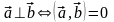 .
.Скалярный квадрат вектора равен квадрату его длины:
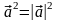 .
.
Определение
3.10.
Углом
между двумя векторами
и
называется
наименьший угол
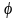 ,
на который нужно повернуть один из них
до совпадения с другим, если эти векторы
отложены из одной точки.
,
на который нужно повернуть один из них
до совпадения с другим, если эти векторы
отложены из одной точки.

Из
определения ясно, что угол
между векторами находится в пределах:
 .
.
Условие ортогональности двух векторов :
или .
Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно,
чтобы сумма произведений соответствующих координат этих векторов была равна нулю.
9. Векторное произведение двух векторов, его свойства и геометрический смысл.
Определение 4.1. Векторным произведением вектора на вектор называется вектор , такой что:
вектор перпендикулярен перемножаемым векторам:
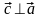 ,
,
 ;
;
2) направление вектора определяется по правилу: если смотреть с конца стрелки вектора на плоскость, образованную векторами и , то вращение (внутри плоскости) от к по кратчайшему пути должно происходить против часовой стрелки;

модуль вектора определяется формулой:
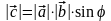 , (1)
, (1)
где - угол между векторами и .
Векторное
произведение обозначается
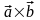 .
.
2. Свойства векторного произведения.
1.
 (антикоммутативность).
(антикоммутативность).
Доказательство:
Из определения следует, что векторы
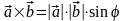 и
и
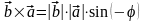 имеют одинаковую длину и противоположные
направления:
имеют одинаковую длину и противоположные
направления:
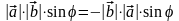 .
.
2.
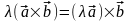 (ассоциативность).
(ассоциативность).
Докажем
это свойство для
:
вектор
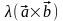 имеет то же направление, что и вектор
.
Вектор
имеет то же направление, что и вектор
.
Вектор
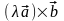 при
имеет то же направление. Длины этих
векторов также совпадают:
при
имеет то же направление. Длины этих
векторов также совпадают:
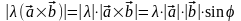 ,
,
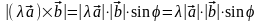 .
Аналогично проводится доказательство
для случая
.
.
Аналогично проводится доказательство
для случая
.
3.
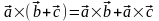 (дистрибутивность).
(дистрибутивность).
Без доказательства.
.6. Геометрический смысл векторного произведения: Модуль векторного произведения равен площади параллелограмма, построенного на перемножаемых векторах.
10. Смешанное произведение трех векторов и его геометрический смысл. Условие компланарности векторов.
Определение 4.3. Векторы, параллельные одной плоскости, называются компланарными. Очевидно, что два вектора всегда компланарны.
Теорема. Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Определение
4.2.
Смешанным
произведением
трех векторов
,
и
называется число, равное
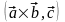 ,
т.е. скалярному произведению векторного
произведения первых двух на третий
вектор.
,
т.е. скалярному произведению векторного
произведения первых двух на третий
вектор.
