
- •1.Матрицы и действия над ними. Умножение матриц.
- •4. Обратная матрица и ее вычисление.
- •5. Система линейных уравнений. Формулы Крамера.
- •6) Матричный метод решения системы уравнений. Метод Гаусса.
- •8. Скалярное произведение векторов и его свойства. Угол между двумя векторами в координатной форме. Условие ортогональности двух векторов.
- •9. Векторное произведение двух векторов, его свойства и геометрический смысл.
- •2. Свойства векторного произведения.
- •10. Смешанное произведение трех векторов и его геометрический смысл. Условие компланарности векторов.
- •4. Свойства смешанного произведения.
- •11. Параметрическое и каноническое уравнения прямой на плоскости.
- •16. Уравнения линий на плоскости. Кривые второго порядка: окружность и эллипс.
- •17. Гипербола и ее каноническое уравнение.
- •18. Парабола и ее каноническое уравнение.
- •19. Полярные координаты на плоскости. Связь между полярными и декартовыми координатами.
- •20. Функция. Способы задания функции. Основные характеристики функции.
- •Определение 1. Абсолютной величиной или модулем действительного числа называется само это число, если и число , если :
- •22. Числовая последовательность и ее предел. Сходимость числовой последовательности.
- •23. Предел функции в точке, предел функции в бесконечности. Бесконечно малые функции. Предел монотонных функций.
- •24. Первый замечательный предел.
- •25. Второй замечательный предел.
- •27. Точки разрывов, их классификация.
- •28. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.
- •29. Производная функции, ее геометрический и физический смысл. Связь между непрерывностью и дифференцируемостью функции.
- •30. Правила нахождения производной: производная произведения и производная частного.
- •32. Производные основных элементарных функций.
- •34. Логарифмическая производная.
- •35. Дифференцирование функций, заданных в параметрической форме. Неявная функция и ее производная.
- •36. Дифференциал функции, его свойства и геометрический смысл. Производные высших порядков.
- •37. Теорема Ферма и теорема Ролля.
- •38. Теорема Лагранжа и теорема Коши.
- •39. Правило Лопиталя раскрытия неопределенностей.
24. Первый замечательный предел.
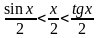 .
.
Разделив
обе части последнего неравенства на
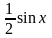 ,
получим:
,
получим:
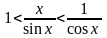 или
или
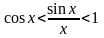 .
.
Эти
неравенства справедливы, как при
 ,
так и при
(т.к. функция
,
так и при
(т.к. функция
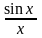 четная). В силу того, что
четная). В силу того, что
 (это видно из рисунка), по лемме о
промежуточной функции, функция
имеет тот же предел при
(это видно из рисунка), по лемме о
промежуточной функции, функция
имеет тот же предел при
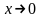 ,
т.е.
,
т.е.
 .
.
25. Второй замечательный предел.
 Предел
(5) называют вторым
замечательным пределом.
Предел
(5) называют вторым
замечательным пределом.
26.
Непрерывность функции в точке. Свойства
непрерывных функций. Определение
1. Функция
называется непрерывной
в точке
,
если функция определена в точке
и в некоторой окрестности, содержащей
эту точку, функция имеет предел при
и этот предел равен значению функции в
точке
: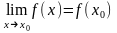 В
этом случае точка
называется точкой
непрерывности функции.
В
этом случае точка
называется точкой
непрерывности функции.
Теорема
1. Если
функции
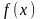 и
и
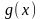 непрерывны в точке
,
то функции
непрерывны в точке
,
то функции
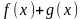 ,
,
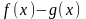 ,
,
 и
и
 непрерывны в точке
.Доказательство:
непрерывны в точке
.Доказательство:
1)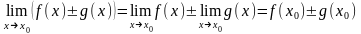 ;2)
;2)
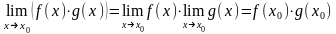 ;
;
3)
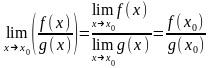 .Теорема
2. Все
основные элементарные функции непрерывны
при всех значениях
,
для которых они определены. Теорема
3. (Непрерывность сложной функции)
Если функция
.Теорема
2. Все
основные элементарные функции непрерывны
при всех значениях
,
для которых они определены. Теорема
3. (Непрерывность сложной функции)
Если функция
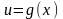 непрерывна в точке
,
а функция
непрерывна в точке
,
а функция
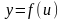 непрерывна в точке
непрерывна в точке
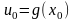 ,
то сложная функция
,
то сложная функция
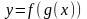 непрерывна в точке
.
непрерывна в точке
.
27. Точки разрывов, их классификация.
Определение
4. Точки,
в которых функция не обладает свойством
непрерывности, или точки, в которых
функция не определена, но в любой
окрестности которых имеются точки
области определения функции, называются
точками
разрыва.
Определение
5. Точка
разрыва
функции
называется точкой
устранимого разрыва,
если существует предел функции в точке
:
,
но
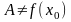 .
Определение
6. Точка
разрыва
функции
называется точкой
разрыва 1-го рода,
если существуют предел слева в точке
.
Определение
6. Точка
разрыва
функции
называется точкой
разрыва 1-го рода,
если существуют предел слева в точке
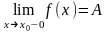 и предел справа
и предел справа
 ,
но они не равны, т.е.
,
но они не равны, т.е.
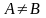 .Определение
7. Точка
разрыва, не являющаяся точкой разрыва
1-го рода, называется точкой
разрыва 2-го рода.В
точках разрыва второго рода не существует
хотя бы один из односторонних пределов.
.Определение
7. Точка
разрыва, не являющаяся точкой разрыва
1-го рода, называется точкой
разрыва 2-го рода.В
точках разрыва второго рода не существует
хотя бы один из односторонних пределов.
28. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.
Определение
8. Функции
называется
непрерывной
на сегменте (отрезке)
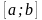 ,
если она непрерывна во всех внутренних
точках этого сегмента, непрерывна справа
в точке
,
если она непрерывна во всех внутренних
точках этого сегмента, непрерывна справа
в точке
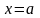 и непрерывна слева в точке
и непрерывна слева в точке
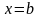 .Теорема
4. (Вейерштрасса)
Если функция
непрерывна на сегменте
,
то она ограничена и достигает своего
наибольшего и наименьшего значения.Теорема
5. (Больцано-Коши)
Если функция
непрерывна на сегменте
и на его концах принимает значения
разных знаков, то внутри этого сегмента
найдется, по крайней мере, одна точка
.Теорема
4. (Вейерштрасса)
Если функция
непрерывна на сегменте
,
то она ограничена и достигает своего
наибольшего и наименьшего значения.Теорема
5. (Больцано-Коши)
Если функция
непрерывна на сегменте
и на его концах принимает значения
разных знаков, то внутри этого сегмента
найдется, по крайней мере, одна точка
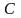 ,
в которой функция равна нулю.Геометрический
смысл теоремы
заключается в следующем: если точки
графика функции
,
соответствующие концам сегмента
,
лежат по разные стороны от оси OX,
то этот график хотя бы в одной точке
сегмента пересекает ось OX.Теорема
6. (О промежуточном значении функции)
Если функция
непрерывна на сегменте
и
,
в которой функция равна нулю.Геометрический
смысл теоремы
заключается в следующем: если точки
графика функции
,
соответствующие концам сегмента
,
лежат по разные стороны от оси OX,
то этот график хотя бы в одной точке
сегмента пересекает ось OX.Теорема
6. (О промежуточном значении функции)
Если функция
непрерывна на сегменте
и
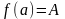 ,
,
 ,
то для любого
,
то для любого
 ,
заключенного между
и
,
заключенного между
и
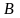 ,
найдется внутри сегмента такая точка
,
найдется внутри сегмента такая точка
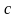 ,
что
,
что
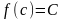 .
Теорема
7. (О существовании обратной функции)
Если функция
непрерывна на сегменте
и возрастает (убывает) на этом сегменте,
то обратная функция
.
Теорема
7. (О существовании обратной функции)
Если функция
непрерывна на сегменте
и возрастает (убывает) на этом сегменте,
то обратная функция
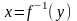 на соответствующем сегменте оси OY
существует и является также возрастающей
(убывающей) функцией.
на соответствующем сегменте оси OY
существует и является также возрастающей
(убывающей) функцией.
