
- •1.Матрицы и действия над ними. Умножение матриц.
- •4. Обратная матрица и ее вычисление.
- •5. Система линейных уравнений. Формулы Крамера.
- •6) Матричный метод решения системы уравнений. Метод Гаусса.
- •8. Скалярное произведение векторов и его свойства. Угол между двумя векторами в координатной форме. Условие ортогональности двух векторов.
- •9. Векторное произведение двух векторов, его свойства и геометрический смысл.
- •2. Свойства векторного произведения.
- •10. Смешанное произведение трех векторов и его геометрический смысл. Условие компланарности векторов.
- •4. Свойства смешанного произведения.
- •11. Параметрическое и каноническое уравнения прямой на плоскости.
- •16. Уравнения линий на плоскости. Кривые второго порядка: окружность и эллипс.
- •17. Гипербола и ее каноническое уравнение.
- •18. Парабола и ее каноническое уравнение.
- •19. Полярные координаты на плоскости. Связь между полярными и декартовыми координатами.
- •20. Функция. Способы задания функции. Основные характеристики функции.
- •Определение 1. Абсолютной величиной или модулем действительного числа называется само это число, если и число , если :
- •22. Числовая последовательность и ее предел. Сходимость числовой последовательности.
- •23. Предел функции в точке, предел функции в бесконечности. Бесконечно малые функции. Предел монотонных функций.
- •24. Первый замечательный предел.
- •25. Второй замечательный предел.
- •27. Точки разрывов, их классификация.
- •28. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.
- •29. Производная функции, ее геометрический и физический смысл. Связь между непрерывностью и дифференцируемостью функции.
- •30. Правила нахождения производной: производная произведения и производная частного.
- •32. Производные основных элементарных функций.
- •34. Логарифмическая производная.
- •35. Дифференцирование функций, заданных в параметрической форме. Неявная функция и ее производная.
- •36. Дифференциал функции, его свойства и геометрический смысл. Производные высших порядков.
- •37. Теорема Ферма и теорема Ролля.
- •38. Теорема Лагранжа и теорема Коши.
- •39. Правило Лопиталя раскрытия неопределенностей.
35. Дифференцирование функций, заданных в параметрической форме. Неявная функция и ее производная.
Теорема
1. Пусть
функция
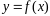 задана параметрически уравнениями
вида:
задана параметрически уравнениями
вида:
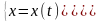 ,где
,где
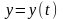 и
и
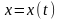 – дифференцируемые функции параметра
– дифференцируемые функции параметра
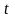 .
Тогда
.
Тогда
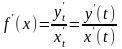 . Если
функция задана неявно уравнением вида:
. Если
функция задана неявно уравнением вида:
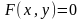 ,
то для нахождения производной такой
функции, проще всего продифференцировать
тождество
,
то для нахождения производной такой
функции, проще всего продифференцировать
тождество
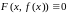 и, убедившись, что производная
входит в получившееся выражение линейно,
найти значение
и, убедившись, что производная
входит в получившееся выражение линейно,
найти значение
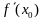 .
.
36. Дифференциал функции, его свойства и геометрический смысл. Производные высших порядков.
Определение
2.
Дифференциалом
функции
в точке
называется главная часть приращения
функции, линейная относительно приращения
независимой переменной. Дифференциал
функции
обозначается
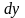 или
или
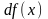 .
.
 . Теорема
2. Для
того, чтобы функция
имела бы в некоторой точке
дифференциал, необходимо и достаточно,
чтобы в этой точке существовала
производная.
. Теорема
2. Для
того, чтобы функция
имела бы в некоторой точке
дифференциал, необходимо и достаточно,
чтобы в этой точке существовала
производная.
Определение
3.
Дифференциал
функции
в точке
есть произведение производной на
дифференциал независимой переменной.Из
формулы (8) следует, что
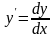 , т.е.
производная функции
в точке
равна отношению дифференциала функции
в этой точке к дифференциалу независимой
переменной.
, т.е.
производная функции
в точке
равна отношению дифференциала функции
в этой точке к дифференциалу независимой
переменной.
Пусть
– абсцисса точки M
на графике некоторой функции
.
Дадим
приращение
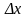 .
N
– точка с абсциссой
.
N
– точка с абсциссой
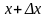 .
Через точку M
проведем касательную MP.
Очевидно, что
.
Через точку M
проведем касательную MP.
Очевидно, что
 ,
,
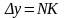 ,
,
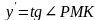 .
Тогда из
.
Тогда из
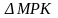 имеем:
имеем: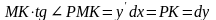 .Таким
образом, дифференциал функции в данной
точке равен приращению ординаты
касательной к графику функции, проведенной
в данной точке при переходе от точки с
абсциссой
к точке с абсциссой
.7.
Свойства дифференциала. 1)
.Таким
образом, дифференциал функции в данной
точке равен приращению ординаты
касательной к графику функции, проведенной
в данной точке при переходе от точки с
абсциссой
к точке с абсциссой
.7.
Свойства дифференциала. 1)
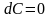 ;2)
;2)
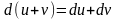 ;3)
;3)
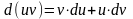 ;4)
;4)
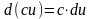 ;5)
;5)
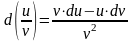 .
.
37. Теорема Ферма и теорема Ролля.
Теорема
Ферма.
Пусть функция
определена на некотором интервале
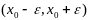 и дифференцируема в точке
.
Тогда, если
является точкой локального минимума
или максимума функции
,
то
и дифференцируема в точке
.
Тогда, если
является точкой локального минимума
или максимума функции
,
то
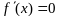 .
.
Теорема
Ролля.
Пусть функция
непрерывна на отрезке
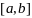 и дифференцируема в каждой точке
интервала
и дифференцируема в каждой точке
интервала
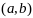 .
Если
.
Если
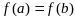 ,
то найдется точка
,
то найдется точка
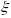 на интервале
,
в которой
на интервале
,
в которой
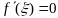 .
.

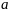
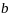
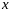
38. Теорема Лагранжа и теорема Коши.
Теорема
Лагранжа.
Пусть функция
непрерывна на отрезке
и дифференцируема в каждой точке
интервала
.
Тогда найдется точка
на интервале
,
в которой
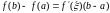 .
.

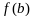
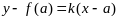
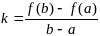
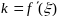
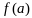
Теорема
Коши.
Пусть функции
и
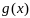 непрерывны на отрезке
и дифференцируемы на интервале
.
Пусть
непрерывны на отрезке
и дифференцируемы на интервале
.
Пусть
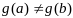 .
Тогда найдется точка
.
Тогда найдется точка
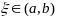 ,
такая что
,
такая что
 .
.
