
- •Высказывания и логические операции над ними.
- •Комплексные числа и формы их представления.
- •Определители и их свойства.
- •Минор и алгебраическое дополнение элемента определителя. Разложение определителя по строке и столбцу.
- •Обратная матрица: определение, построение и свойства. Решение матричных уравнений.
- •Системы линейных уравнений. Совместные и эквивалентные системы. Элементарные преобразования системы.
- •Теорема Кронекера-Капелли. Схема разрешимости произвольных систем линейных уравнений. Свободные и базисные переменные.
- •2) , , Компланарны
- •Произв. Ф-и в точке:определение, геометрич. И механич. Смысл. Уравнение касательной.
- •Асимптоты графика функции и их нахождение
- •Функции нескольких переменных. Частные производные.
2) , , Компланарны
![]()
В ывод
уравнения плоскости в пространстве.
Нормаль. Расстояние от точки до плоскости.
Угол между плоскостями. Условия
параллельности и перпендикулярности
плоскостей.
ывод
уравнения плоскости в пространстве.
Нормаль. Расстояние от точки до плоскости.
Угол между плоскостями. Условия
параллельности и перпендикулярности
плоскостей.
Точка M0
и нормаль
![]() однозначно
определяют плоскость
однозначно
определяют плоскость
![]()
Пусть
![]() - произвольная точка искомой плоскости.
- произвольная точка искомой плоскости.
![]()
![]() - векторное уравнение
плоскости
- векторное уравнение
плоскости
![]()
![]()
![]()

Расстояние от точки
![]() до плоскости
до плоскости
![]() :
:
![]()
Углы между плоскостями
– углы между нормалями:
![]()
Условие параллельности
плоскостей:![]()
Условие
перпендикулярности плоскостей:
![]()
Вывод канонического уравнения прямой в пространстве. Формы задания прямой. Угол между прямыми. Условия параллельности и перпендикулярности прямых в пространстве.
Пусть - произвольная точка искомой прямой.
![]()
![]()
![]()
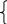 - параметрическое
уравнение прямой, (t – параметр)
- параметрическое
уравнение прямой, (t – параметр)
![]()
Уравнение прямой
AB:
![]()
![]()

![]()
Прямая как линия пересечения плоскостей.
Угол между прямыми
![]()
Условие параллельности
прямых:
![]()
Условие
перпендикулярности прямых:
![]()
Взаимное расположение прямой и плоскости в пространстве. Условия параллельности и перпендикулярности прямой и плоскости.
Взаимное расположение прямой и плоскости в пространстве.
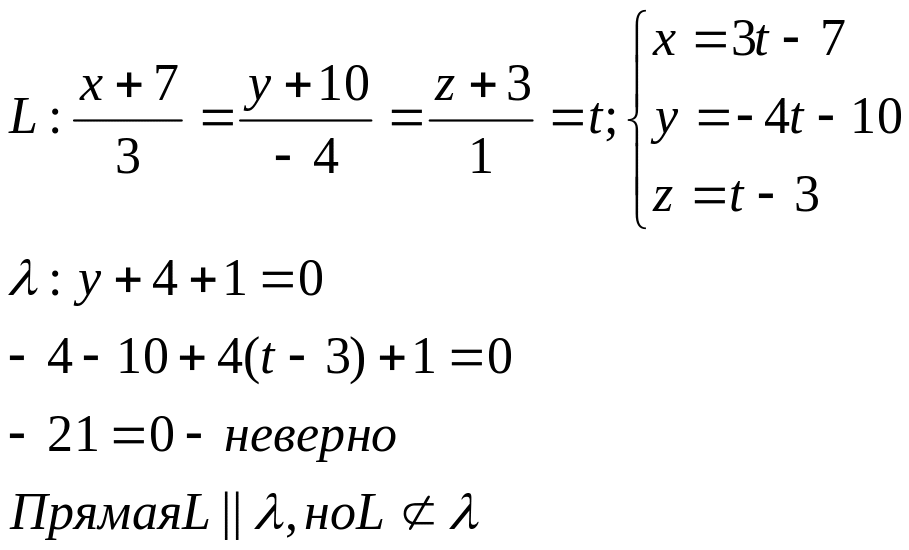
Угол между плоскостью и прямой:
![]() ;
;
Условие параллельности плоскостей:
![]() ;
;
Условие перпендикулярности плоскостей:
![]() ;
;
Поверхности 2 порядка и их сечения: эллипсоид и конус.
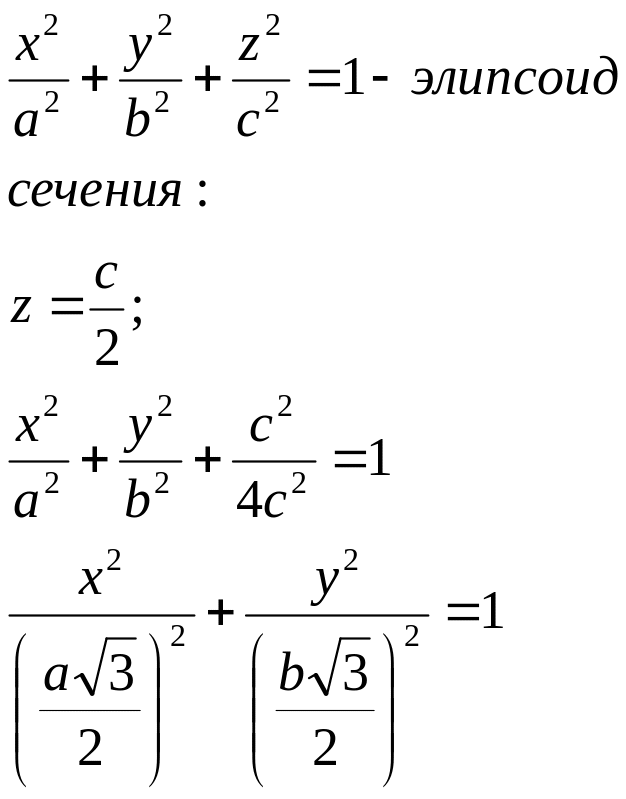
![]()
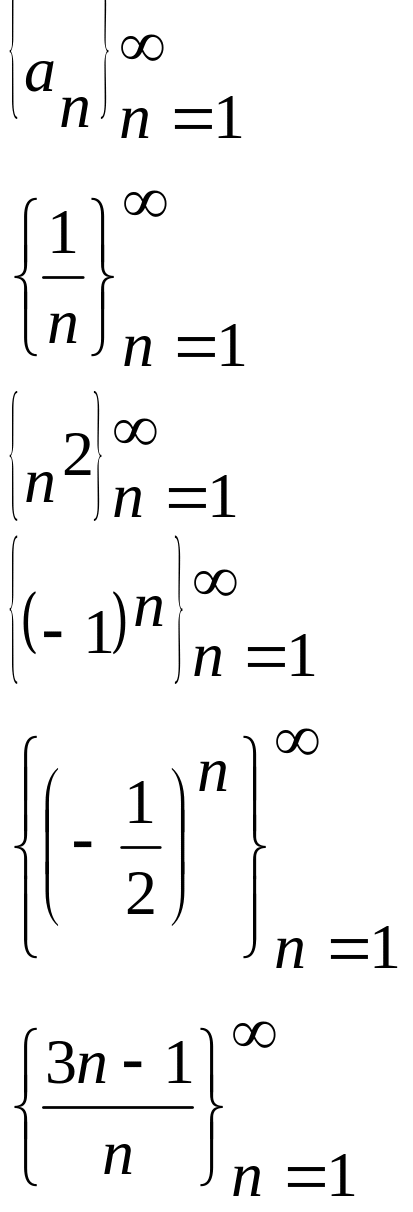
Z=0:
![]() -
эллипс в
плоскости z=c\2
-
эллипс в
плоскости z=c\2
X=0:![]() эллипс в плоскости x=0
y=0
эллипс в плоскости x=0
y=0
![]()
![]() :
Конус
:
Конус
Сечения:
Z=0:
![]() точка
(0;
0; 0)
точка
(0;
0; 0)
Z=+-c:
![]()
Z=+-2c:
![]()
X=0:
![]()
Y=b:
![]()
Поверхности 2-го порядка и их сечения:
Однополостный и двуполостный гиперболоиды.
Однополостный гиперболоид
![]()
Сечения:![]() Эллипс
Эллипс
Двуполостный гиперболоид
![]()
С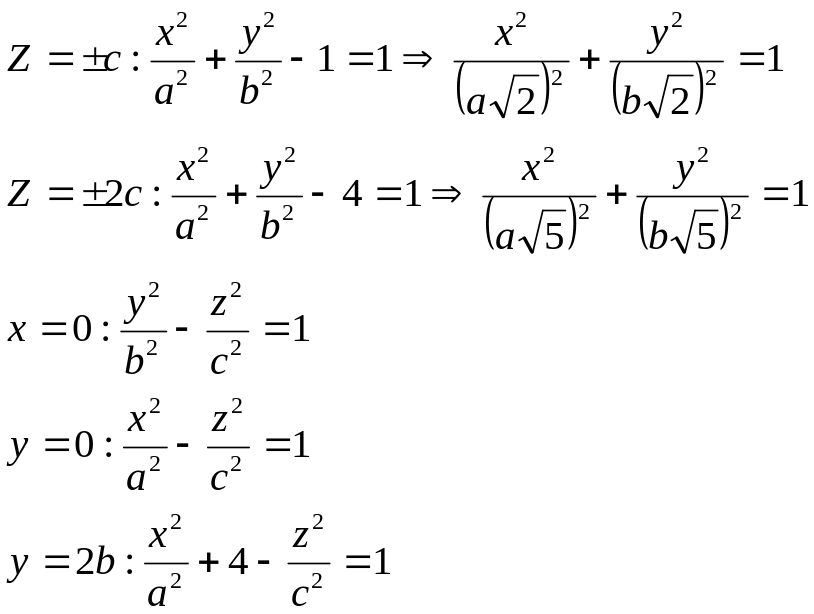 ечения:
ечения:![]() точки
(0;0;c) и (0;0;-c)
точки
(0;0;c) и (0;0;-c)
![]() -эллипс
-эллипс
![]()
Поверхности 2-го порядка и их сечения:
Эллиптический и гиперболический параболоиды.
Эллиптический параболоид
![]()
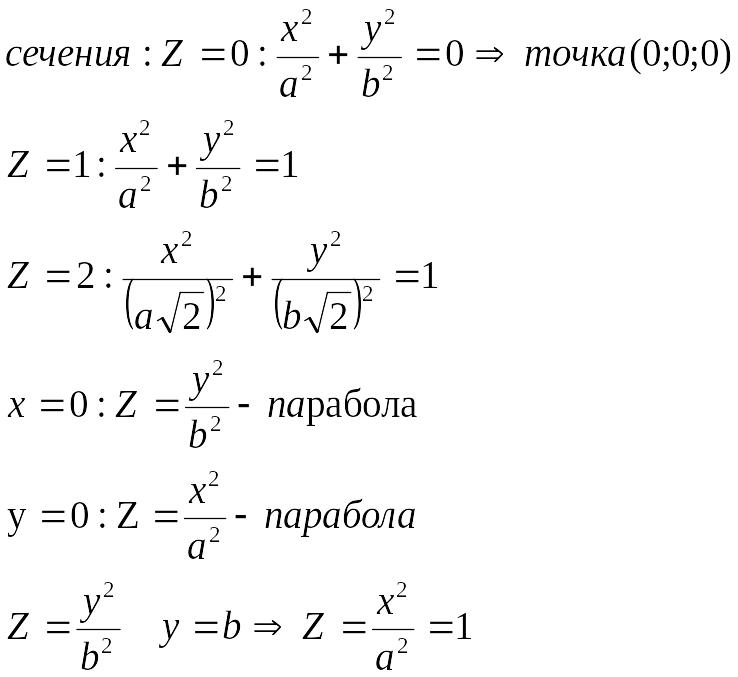
Гиперболический параболоид
![]()
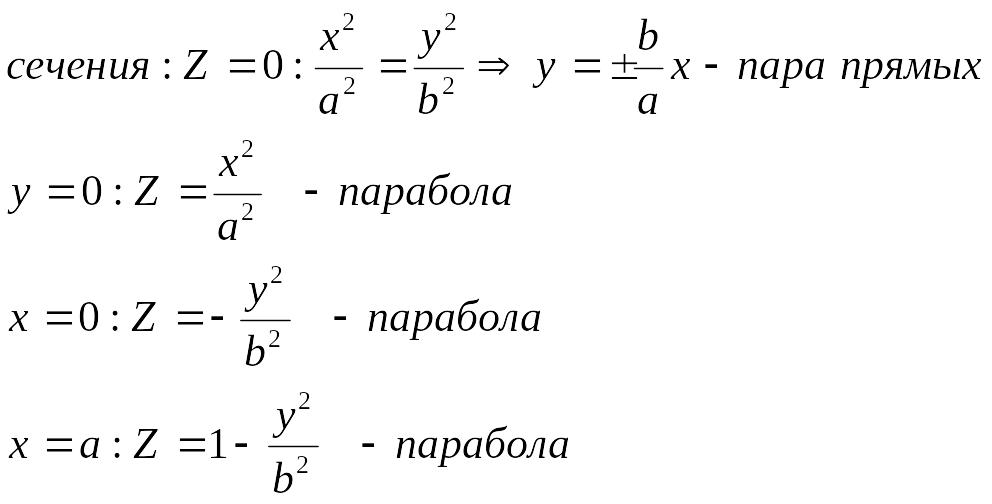
Понятие и примеры числовых последовательностей. Монотонные и ограниченные последовательности. Предел числ. послед-сти.
Числ. последовательность называется функция, заданная на множестве натур. чисел N. F(n)=an – общ. член числ. послед.
: 1; 1/2; 1/3; 1/4; …; 1/100… 0
n ∞
: 1;4;8;16;… ;100… ∞
n ∞
: -1;1;-1;1… нет предела
: -1/2;1/4;-1/8;1/16;… 0
n ∞
: 2;5/2;8/3;11/4; … 3
n ∞
 a1 a2
0 a3
a1 a2
0 a3
x
-1/2 -1/8 1/16 1/4
![]()
Число а назыв-ся
пределом числовой послед-сти
![]() (Lim an=A)
,
(Lim an=A)
,

 n∞
n∞
если E>0 N такой, что n>N выполняется (an-A)<E (разность сколько угодно мала).
Числ. посл., имеющая конечный предел называется сходящейся (в прот. случае расходящейся).
Св-ва ч.п.:
1) монотонность: an>an+1 – убывающая
an≥an+1 – невозр.
аn<an+1 – возраст.
an≤an+1 – неубывающ.
2) огран-сть: M >0, что (an) ≤M.
аn=1/n – убывающ.
(1/n) ≤1 – ограничен.
аn=(-1/2) n – немонотонна
((-1/2)n) ≤1/2 – ограничена
аn=2 n – возраст. и неогр.
Бесконечно малые и б.б. числовые последовательности, связь между ними.
Теорема 1. : Сходящаяся числ. последовательность ограничена.
Т.2: Ограниченная монотонная ч. п. сходится.
Если Lim an=0 , то ч.п. называется б.м.
Пример:
![]() ;
;
![]() ;
;
![]() .
.
Ч.п. называется б.б. и обознач.: Lim an=∞

 n∞
n∞
е сли:
M>0 N такой, что n>N, выполняется:
(an)>M.
сли:
M>0 N такой, что n>N, выполняется:
(an)>M.
пример:
![]() ;
;
![]() .
.
Т.3:
А) если
- б.м. ч.п. и an≠0,
то
 - б.б. ч.п. [1/0=∞]
- б.б. ч.п. [1/0=∞]
Б) если
![]() - б.б. ч.п. и bn
≠0, то
- б.б. ч.п. и bn
≠0, то
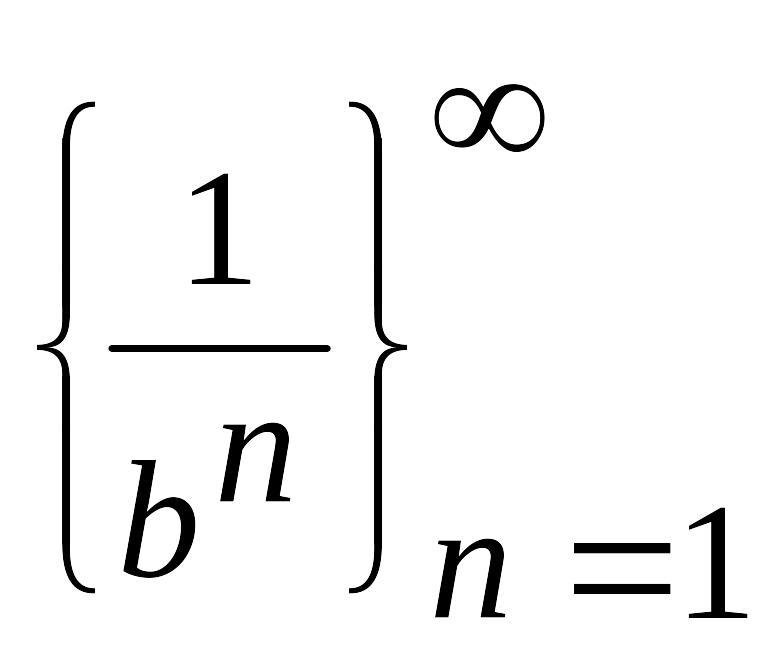 - б.м. ч.п. [1/∞=0].
- б.м. ч.п. [1/∞=0].
Предел ф-ции(2 опред.):
1-ое опред.(на языке
последовательностей(по Гейне)): Число
А наз-ся пределом ф-ции f(x) в точке X0![]() ,
если
,
если
![]() на множестве X выполняется:
на множестве X выполняется:
![]()
![]()
2-ое опред.(на языке
![]() (эпсилам-дельта)
по Коши):
(эпсилам-дельта)
по Коши):
![]() ,
если:
,
если:
![]()
Односторонние пределы и пределы по бесконечному направлению
Односторонние пределы:
1)
![]()
![]()
Теорема 1: Оба определения предела ф-ции в точке эквивалентны.
Теорема 2: Предел ф-ции X0 тогда и только тогда, когда существуют оба односторонних предела и они равны между собой.
![]()
Пределы по бесконечному направлению:
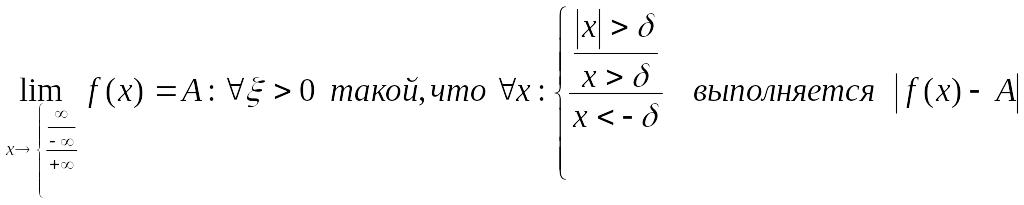
1) Если
![]()
![]()
2) Ф-ция
![]() :
:
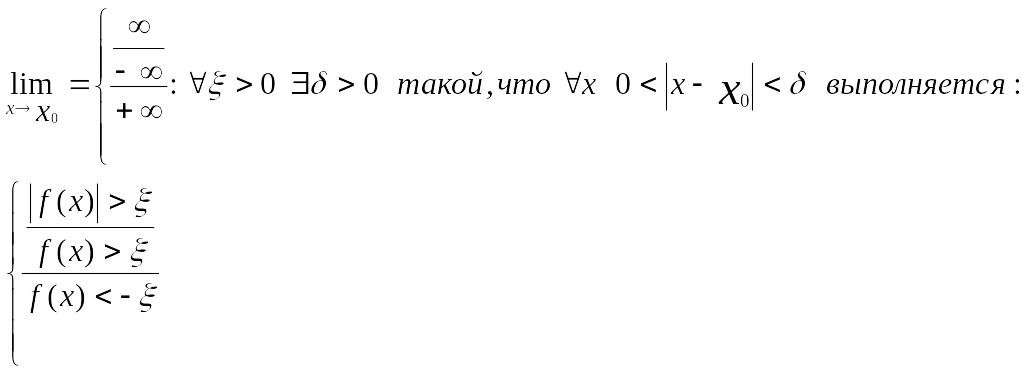
Бесконечно малые и бесконечно большие ф-ции в точке, их св-ва:
1) Если
2) Ф-ция :
Свойства:
Теорема 1:
1) Если f(x)-б.м. ф-ция
в т.![]()
2) Еслиg(x)-б.б. ф-ция
в т.
![]()
![]()
Теорема 2:
Если
![]()
Теорема 3:
Сумма, разность и произведение б.м. ф-ций в т.X0 является б.м. ф-цией в т. X0.
Произведение б.м. в т. X0 на ограниченную, явл. б.м.
Теорема о пределах ф-ции в точке:
Если
![]() :
:
1)
![]()
2)
![]()
3)
![]()
Классификация бесконечно малых функций
Пусть
![]() и
и
![]() .
.
Вычисляем
![]() .
.
Если
![]() ,
то
,
то
![]() -
бесконечно малая функция более высокого
порядка малости, чем
-
бесконечно малая функция более высокого
порядка малости, чем
![]() .
Пример
.
Пример
![]()
Если
![]() ,
то
,
то
![]() -
б.м. функции эквивалентны в т. X0
-
б.м. функции эквивалентны в т. X0
Если
![]() ,
то
,
то
![]() и
и
![]() -
одного порядка малости в т. X0.
Пример 5x2и3x2.
-
одного порядка малости в т. X0.
Пример 5x2и3x2.
Замечательные пределы
1-й замечательный предел:
Пример:
![]()
1)![]()
2)![]()
3)![]()
2-й замечательный предел:
![]()
Пример:
![]()
Непрерывность ф-и в точке. Классиф. точек разрыва. Св-ва ф-й, непрерывность в точке и на отрезке.
Y=f(x) по обл Д Xo €Д Xo+∆X€Д ∆X – приращение аргумента
∆f(x)=f(Xo+∆X) – f(Xo) - приращение ф-и в точке Xo
Ф-я y=f(x),
наз. Непрерывной в точке Xo
если: 1) Xo€Д
т.е. ![]() f(Xo);
2)
f(Xo);
2) ![]() ;
3)
;
3) ![]() (б.м. приращение по аргументу
(б.м. приращение по аргументу ![]() соотв. Б.м. приращение аргумента ∆f)
соотв. Б.м. приращение аргумента ∆f)
Точки в которых нарушается непрерывность, наз. точками разрыва.
Классиф. точек разрыва: Вычислим: пусть Хо – т.разрыва, f(Xo-0) и f(Xo+0) – односторонние пределы.
1)Если однос.пределы f(Xo-0)=A и f(Xo+0)= В – конечны, то Хо наз.точкой разрыва 1-го рода.
2)В частности, если А=В(но ≠f(Хо), то Хо, наз.точкой устранённого разрыва.
3

 )Все
остальные точки разрыва(хотябы один из
одност. пределов бесконечны или не
сущ.)и точки разрыва 2-го порядка.
)Все
остальные точки разрыва(хотябы один из
одност. пределов бесконечны или не
сущ.)и точки разрыва 2-го порядка.


 F(x)
=
F(x)
= ![]()
Х
 =0,т.разрыва
2-го рода F(x)=
=0,т.разрыва
2-го рода F(x)=![]() F(x)=
F(x)=
![]() f(x)=
f(x)=![]()
X=0,т.разрыва 1-го рода x=0, т.устран.разрыва x=1, точка непрерывности
Ф-я f(x) наз.непрер.на отрезке АВ, если она непрерывна в каждой т.этого отрезка.
С
 в-ва
ф-й, непрер.на отрезке: Т1(Вейерштрасса):если
ф-я f(x)
непрер.на отрезке АВ, то она достигает
на этом отрезке наибол.(М) и наимен.(м)
значений.
в-ва
ф-й, непрер.на отрезке: Т1(Вейерштрасса):если
ф-я f(x)
непрер.на отрезке АВ, то она достигает
на этом отрезке наибол.(М) и наимен.(м)
значений.
Т
 2:
если ф-я непрер. На отрезке АВ и принимает
на концах отрезка значение разных
знаков, т.е. f(a)*f(b)<0,то
сущ. C€(a,b)
такой, что f(c)=0
2:
если ф-я непрер. На отрезке АВ и принимает
на концах отрезка значение разных
знаков, т.е. f(a)*f(b)<0,то
сущ. C€(a,b)
такой, что f(c)=0
Т
 3:
если ф-я f(x)
непрер. На отрезке АВ и приним. значение
между м и М, то для любого числа C€(a,b)
такое, что f(c)=c
3:
если ф-я f(x)
непрер. На отрезке АВ и приним. значение
между м и М, то для любого числа C€(a,b)
такое, что f(c)=c
Т еорема:
все остальн. Элементы ф-и( степенная,
показательная, логарифмическая, тригоном.
и обратн. тригоном)непрер. на своей
облости определения. Пример: док-ть, что
ф-я f(x)=2+3x-x2
непрер. на(-∞;+∞)
еорема:
все остальн. Элементы ф-и( степенная,
показательная, логарифмическая, тригоном.
и обратн. тригоном)непрер. на своей
облости определения. Пример: док-ть, что
ф-я f(x)=2+3x-x2
непрер. на(-∞;+∞)
2’)![]() ;
;
![]()
