
Упражнение 45.
Подберите соответствующее с; каким его надо взять? Найдите выражение корней исходного уравнения через параметры p и q. Подкоренное выражение, от знака которого зависит как наличие, так и количество вещественных корней у уравнения, называется дискриминантом (приведённого) квадратного трёхчлена.

Попутно мы можем сделать один весьма важный вывод: параболы - графики Г(р,q) всех приведённых квадратных трёхчленов конгруэнтны, причём относительно одной только группы параллельных переносов – их даже поворачивать (тем более, отражать) не надо!
В терминах действия групп на множествах, можно сказать, что группа трансляций действует на множестве таких парабол транзитивно: все они лежат на одной орбите.
А как влияет на вид параболы старший коэффициент неприведённого квадратного трёхчлена? Для ответа достаточно посмотреть в тетрадь для 6-го класса. Так что полезно хранить тетради.
Вот вы и научились решать квадратные уравнения – теперь достаточно подставлять числа в готовую формулу. А на уроках мы научимся решать и системы уравнений с квадратными уравнениями и уравнения, сводящиеся к квадратным заменой переменной.
Приступим к знакомству с последними из элементарных функций (функций, которые проходят в школе) – тригонометрическим функциям и обратным к ним.
Вначале, пока у нас были только целые числа, мы имели только целочисленную плоскость ZZ и могли рисовать линии, состоящие только из отдельных точек. Затем у нас появились рациональные числа, и мы стали рисовать графики на рациональной плоскости QQ непрерывными линиями, хотя по-прежнему не имели ещё на это права.
И вот, теперь, на вещественной плоскости RR мы, наконец, с чистой совестью можем это делать. Правда, мы ещё пока не можем строго доказывать такие факты, как, например, то что «непрерывная кривая», соединяющая точки А и С квадрата АВСD пересекает аналогичную кривую, идущую из В в D. Мы это с лёгкостью сделаем, как только построим соответствующий технический аппарат. А пока что примем такие, наглядно очевидные, вещи на веру. Например, то, что луч, выходящий из начала координат, пересекает окружность с центром в начале координат.
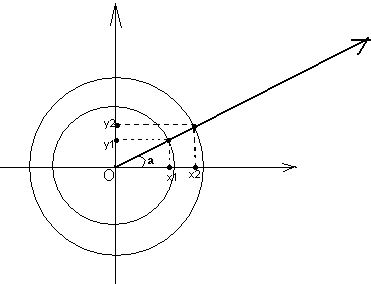
Если мы будем рисовать концентрические окружности с центром в О, то отношение ординат точек пересечения луча с ними к их радиусам остаётся величиной неизменной (почему?), зависящей только от угла а и поэтому может быть принято за его меру. В качестве окружности можно выбрать, например, окружность с радиусом, равным единице, и тогда это отношение просто будет равным ординате.
Def. Углом =(a,b) между лучом ОА=a и ОВ=b называется часть плоскости, заметаемая лучом а, поворачивающимся вокруг вершины О против часовой стрелки до совмещения с углом b.
Упражнение 46. Объясните, почему из этого определения следует -=(b,a)
Def. Пусть на декартовой плоскости с осью абсцисс ОХ=а задан луч ОС=b. Тогда синусом угла =(a,b) называется ордината y его точки A пересечения с единичной окружностью, косинусом – абсцисса x этой точки A и тангенсом – отношение ординаты этой точки к её абсциссе. Обозначения соответственно, sina, cosa и tga.
Иными словами, если А(х,у) – точка на единичной окружности, в которой луч, составляющий угол с осью абсцисс ОХ, встречает окружность единичного радиуса с центром в начале координат О декартовой плоскости ХОУ, то тригонометрические функции угла =АОХ определяются так: sin=y, cos=x, tg=y:x.
Угловыми единицами измерения являются градусы и радианы. Условились считать полный оборот луча вокруг его вершины принять за 360. Тогда развёрнутому углу соответствует 180, прямому - 90 и т.д. В то же время «длина» окружности единичного радиуса, измеренная экспериментально, даёт результат примерно 6,28. Хорошим приближением для неё служит обыкновенная дробь 44/7. На самом деле, определив аккуратно понятие длины кривой (в том числе и окружности), можно доказать, что число это иррационально и, более того, трансцендентно (то есть не может служить корнем никакого многочлена с целыми коэффициентами). Например, не может быть получено в результате последовательного выполнения арифметических действий и возведений в любые рациональные степени. Как вы уже знаете, число это принято обозначать, как 2. Раньше это могло вызвать определённый дискомфорт, ибо «число» это оказывалось вне имевшейся у вас в наличии числовой системы (Q). Сейчас же это не должно вас смутить, особенно после прочтения «лирического отступления о десятичных дробях». Итак, каждому углу соответствует точка А пересечения его луча, отличного от ОХ, с единичной окружностью, а этой точке – длина дуги ЕА окружности, считая от точки Е(1,0) до А против часовой стрелки. Таким образом, углу 360° соответствует вся окружность – радианная мера такого угла равна как раз 2. Радианная мера развёрнутого угла ровно p, прямого угла -p:2 и т.д.
У глы
в тригонометрии принято считать в
радианах, так что sin1 –
это не синус угла в 1°
(почти ноль), а синус угла, чуть меньшего,
чем p:3=60°.
глы
в тригонометрии принято считать в
радианах, так что sin1 –
это не синус угла в 1°
(почти ноль), а синус угла, чуть меньшего,
чем p:3=60°.
Упражнение 47.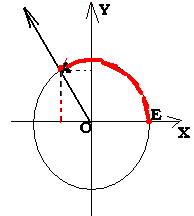
Исходя из данных определений и положений точек на тригонометрической (единичной) окружности, считая, что для некоторого данного угла a, 0a/2 sin a=a, cos a=b найти значения: a) sin(-a); cos(-a) b) sin(p+a); cos(p+a)
Упражнение 48.
В условиях предыдущего упражнения (и исходя из его результатов!), найдите sin(p-a); cos(p-a). Найдите значения функций sin a, cos a для a=0, p/2, p.
Тригонометрические функции |
Значения угла |
||
/6 |
/4 |
/3 |
|
sin a |
|
|
|
cos a |
|
|
|
tg a |
|
|
|
Если мы меряем углы в радианах, то длина пройденной нами дуги окружности может быть сколь угодно велика – мы, как велосипедисты на стадионе, наматываем круги, а спидометр показывает пройденное расстояние. Поэтому функции sin и cos определены на всей числовой оси (R); имеют смысл, например, такие выражения, как sin44 или cos(-7,12). Однако, обе они – периодические. Чему равен их минимальный период? Чему равен (минимальный) период функции tg? Кстати, всюду ли она определена?
Упражнение 49.
Докажите, что хR y, 0y/2 такой, что один из углов - либо x, либо (-x), либо (-x), либо (+x) y(mod2).
Таким образом, синус и косинус любого угла можно выразить через синус или косинус соответствующего острого угла – угла, образованного лучом, исходящим из начала координат и пересекающего окружность(с центром в начале координат) в первом квадранте Декартовой плоскости. Соберите вместе результаты упражнений 2 и 47-49 и докажите основное тригонометрическое тождество:
Упражнение 50.
Докажите, что хR имеет место sin2x+cos2x=1
Упражнение 51.
Теперь вспомнив факт из геометрии – о соотношении гипотенузы и катета, лежащего напротив угла 30 (=/6) в прямоугольном треугольнике (а если забыли, то выведите заново, достроив до равностороннего треугольника), заполните следующую таблицу (значениями соответствующих тригонометрических функций):
Упражнение 52.
Скомбинировав результаты упражнений 46,47 и 49, набросайте эскизы (по точкам, в которых уже известны значения функций, соединяя их плавными дугами) графиков функций y=sinx, y=cosх и y=tgx.
Упражнение 53.
С оставьте
матрицу линейного оператора - поворота
на угол a - в стандартном
базисе (1,0); (0,1). Составьте такую же матрицу
для поворота на угол .
Теперь составьте третью матрицу – для
поворота на угол +.
Поскольку этот же поворот можно получить
последовательным выполнением первых
двух, то получаем матричное уравнение
(составьте его). Из него выведите формулы
сложения: sin(),
cos(),
tg (a±b).
оставьте
матрицу линейного оператора - поворота
на угол a - в стандартном
базисе (1,0); (0,1). Составьте такую же матрицу
для поворота на угол .
Теперь составьте третью матрицу – для
поворота на угол +.
Поскольку этот же поворот можно получить
последовательным выполнением первых
двух, то получаем матричное уравнение
(составьте его). Из него выведите формулы
сложения: sin(),
cos(),
tg (a±b).
Упражнение 54.
Исходя из результатов предыдущего
упражнения, выведите формулы для .![]() .
Какие выводы отсюда можно сделать
относительно графиков функций y=sinx
и y=cosх?
.
Какие выводы отсюда можно сделать
относительно графиков функций y=sinx
и y=cosх?
Выведите формулы для двойного и тройного углов: sin2a=, cos2a=, tg2a=, sin3a=, cos3a= (справа от знака равенства должны стоять выражения, содержащие только sina, cosa и tga)
Упражнение 55. Охарактеризуйте все три тригонометрические функции с точки зрения периодичности, чётности/нечётности, монотонности. Каковы их области значений (Range)?
У тригонометрических функций не может
быть обратных к ним на всей их области
определения. Кстати говоря, почему?
Поэтому для них выделены области, где
эти функции могут быть определены.
Для функции y=sinx
это отрезок
![]() ,
для y=tgx это
интервал
,
для y=tgx это
интервал
![]() ,
а для y=cosx
это отрезок [0,]. Это
также как с у=х
– там нам пришлось для однозначности
обратной функции выбрать одну из двух
ветвей параболы (верхнюю) и назвать её
арифметическим значением корня. Мы
брали обратную к функции у=х2 на
участке х0 её области
определения. Здесь ситуация и того хуже:
приходится выбирать одну из уже
бесконечного множества ветвей. Обратные
функции имеют приставку arc
к соответствующей функции, указанные
области называются областями их
главных значений.
,
а для y=cosx
это отрезок [0,]. Это
также как с у=х
– там нам пришлось для однозначности
обратной функции выбрать одну из двух
ветвей параболы (верхнюю) и назвать её
арифметическим значением корня. Мы
брали обратную к функции у=х2 на
участке х0 её области
определения. Здесь ситуация и того хуже:
приходится выбирать одну из уже
бесконечного множества ветвей. Обратные
функции имеют приставку arc
к соответствующей функции, указанные
области называются областями их
главных значений.
Упражнение 56.
Постройте графики всех этих функций (arcsinx, arccosx, arctgx). Постройте затем графики следующих функций, предварительно установив их области определения (Domain):
y=sin(arcsinx), y=arcsin(sinx), y=cos(arccosx), y=arccos(cosx),
y=arctg(tgx), y=tg(arctgx). Вычислите sin(arccos(-x))
Упражнение 57.
Напишите уравнение окружности с центром в точке О(a,b) и радиусом r.
Упражнение 58.
Напишите уравнение произвольной касательной к этой окружности (касающейся её в точке (u,v)).
Упражнение 59.
Напишите уравнение касательной к этой окружности, проведённой из начала координат.
Напишите уравнение касательной к этой окружности, проведённой из произвольной точки (u,v).
Упражнение 60.
Приведенному
квадратному уравнению
![]() на плоскости параметров (p;q)
соответствует
точка. Отметьте на плоскости параметров
(p;q)
множества
точек, соответствующих следующим
условиям:
на плоскости параметров (p;q)
соответствует
точка. Отметьте на плоскости параметров
(p;q)
множества
точек, соответствующих следующим
условиям:
уравнение имеет единственный корень (совпадающие корни),
не имеет корней,
имеет два корня,
имеет два корня разных знаков,
имеет два положительных корня,
имеет корень равный нулю,
имеет два корня равные по модулю.
Упражнение 61.
Отметьте на плоскости параметров (p;q) множества точек, соответствующих уравнениям, один из корней которых
равен 1,
равен -3.
Постарайтесь получить общее утверждение.
Упражнение 62.
Нарисуйте на
плоскости (p;q)
линии,
соответствующие уравнению
![]() для разных значений константы. Что
получилось и почему?
для разных значений константы. Что
получилось и почему?
Упражнение 63.
Нарисуйте на
плоскости (p;q)
линии,
соответствующие уравнению
![]() для разных значений константы.
для разных значений константы.
Упражнение 64.
Проведите
исследование количества корней уравнения
![]() на плоскости (p;q).
на плоскости (p;q).
Упражнение 65.
Сколько решений в зависимости от значений параметра а имеет система уравнений:
![]()
Упражнение 66.
Обоснуйте следующие формулы для нахождения корней уравнения ах2+вх+с=0
Если a+b+c=0, то х1=1, х2=
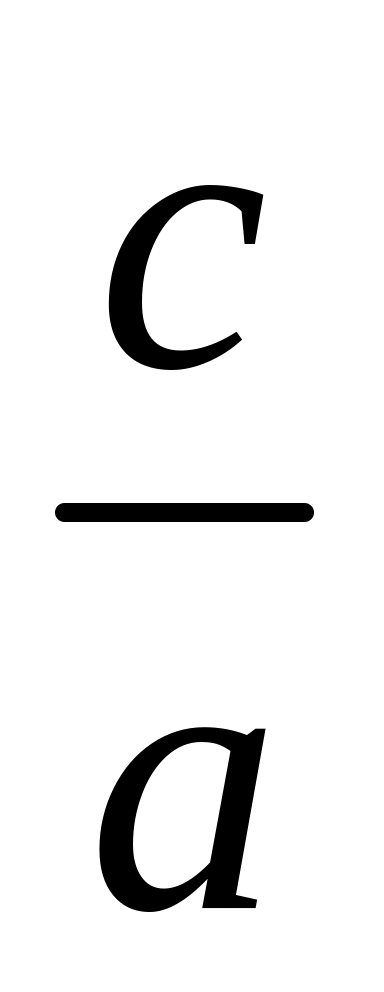 ;
;Если a-b+c=0, то х1=-1, х2=- .
Упражнение 67.
Составьте квадратное уравнение, имеющее следующие корни: х1=2-3, х2=2+3.
Упражнение 68.
Найдите правильную дробь, которая, при увеличении знаменателя на 3 и возведения числителя в куб, увеличивается в 3 раза.
Упражнение 69.
Выведите следующие тригонометрические формулы:
tg();
coscos (substitute =u+v, =u-v);
sinsin;
coscos=____;
sinsin=____;
sincos=____
Соберите все тригонометрические формулы вместе, составьте из них шпаргалку, распечатайте её и наклейте в тетрадь так, чтобы удобно было ею пользоваться.
Рассмотрим уравнение sinx=a.
Если |a|>1, то решений (во множестве R вещественных чисел) нет. При а=0 х=k, kZ.
При а=1, x=![]() +2k,
kZ.
При а(-1,0)(0,1)
x=arcsina+2k
и x=-arcsina+2k,
kZ..
Обе последние серии решений можно
объединить в одну формулу: х=(-1)karcsina+k.
+2k,
kZ.
При а(-1,0)(0,1)
x=arcsina+2k
и x=-arcsina+2k,
kZ..
Обе последние серии решений можно
объединить в одну формулу: х=(-1)karcsina+k.
Решите уравнения:
Упражнение 70.
cos2x=1-sinx.
Следующее уравнение – однородное, оно приводится к квадратному уравнению относительно тангенсов:
Упражнение 71.
5sin2x-4sinxcosx-cos2x=4
Упражнение 72.
4-cos(2(13x+9)2)=5sin((13x+9)2).
Упражнение 73*.
![]()
Упражнение 74.
sinx+sin5x=0 (Answer: two series, first x=/4+k/2, second x=k/3, kZ)
Упражнение 75.
sin2x+sin23x=1 (Answer: two series, first x=/8+k/4, second x=/4+k/2, kZ)
Метод решения тригонометрических уравнений с помощью введения дополнительного угла основан на следующем упражнении:
Упражнение 76.
Докажите, что a,bR | cos=
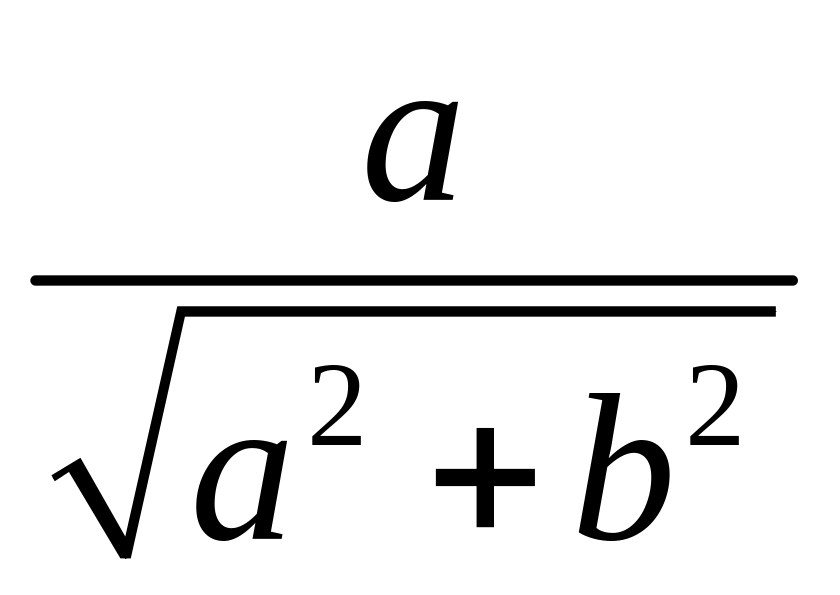 ,
sin=
,
sin=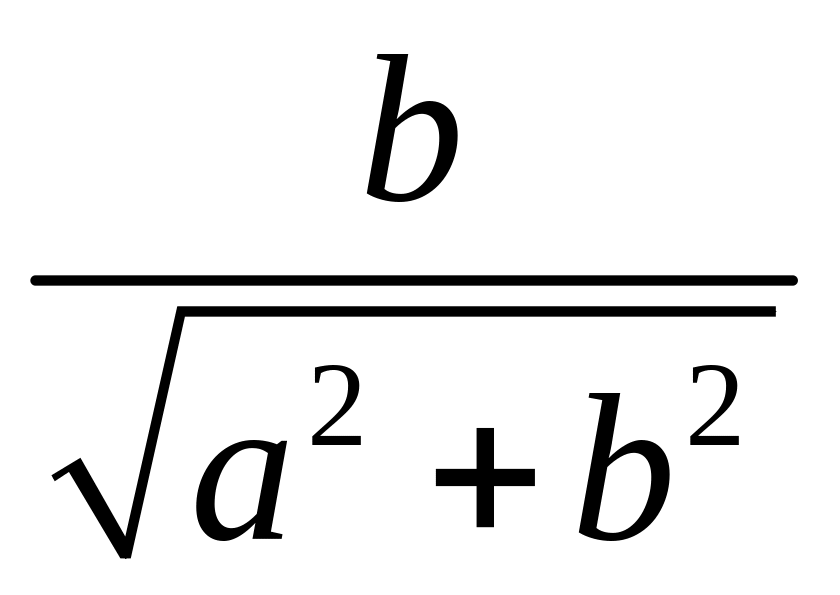 ;
;Докажите, что в случае
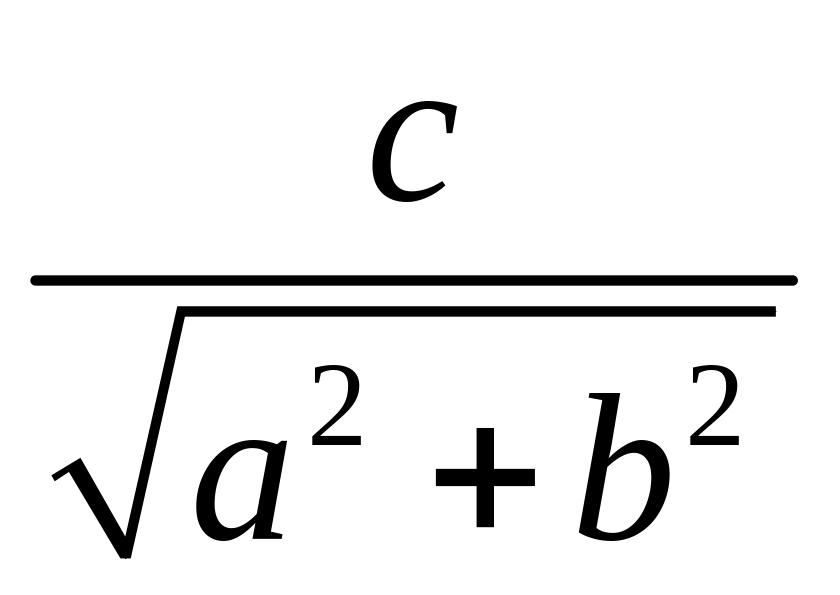 [-1,1],
решением уравнения coscosx+sinsinx=
является x=arccos
+2k.
В иных случаях у этого уравнения
(вещественных) решений нет.
[-1,1],
решением уравнения coscosx+sinsinx=
является x=arccos
+2k.
В иных случаях у этого уравнения
(вещественных) решений нет.
Упражнение 77.
Основываясь на предыдущем упражнении, решите уравнение sinx+3cosx=1.
Решите уравнения:
Упражнение 78.
2sin2x+3cosx=0; (Answers: /2+n, (-1)narcsin(3/4)+n)
2cos2x+3sinx=0; (Answers: (-1)n/6)+n)
sin3x-sinx+cos2x=1; (Answers: n, -/2+2n, (-1)n/6)+n)
sinx-sin3x=cos2xsin3x. (Answers: /4+n/2)
Упражнение 79.
2sin2x+cos-2x=3; (Answers: /4+n/2)
cosx-2sin2xsinx-4cos2x-4sin2x=0; (Answers: /2+n, 2/3+2n)
2cos2x-1=(2cos2x+1)tgx; (Answers: -/4+n, (-1)n/12+n/2)
(cosx-sinx)(1+0,5sin2x)+sinx=2cos2x (Answers: p/2+pn)
Упражнение 80.
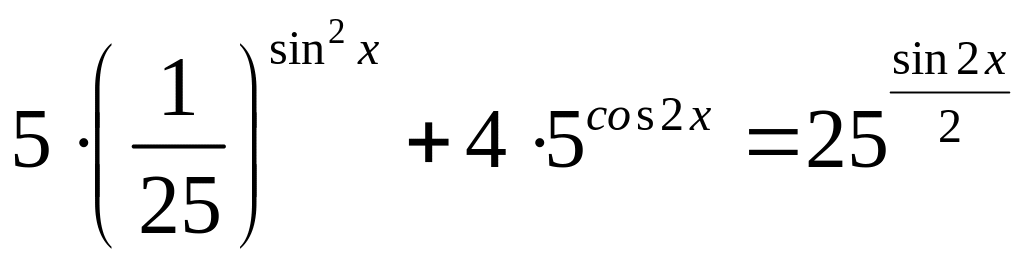 ; (Answers:
p/2+pn)
; (Answers:
p/2+pn)sin4x+cos4x=sin2x; (Answers: 0,5(-1)narcsin(3-1)+n/2)
(2cosx-sinx-2)(sinx-1)=cos2x ; (Answers: p/2+2pn, /3+2n)
4cos4x+6sin22x+5cos2x=0 (Answers: ±p/3+pn)
Упражнение 81.
|sinx+cosx|=1+2sin2x; (Answers: pn/2)
sin6x+cos6x=
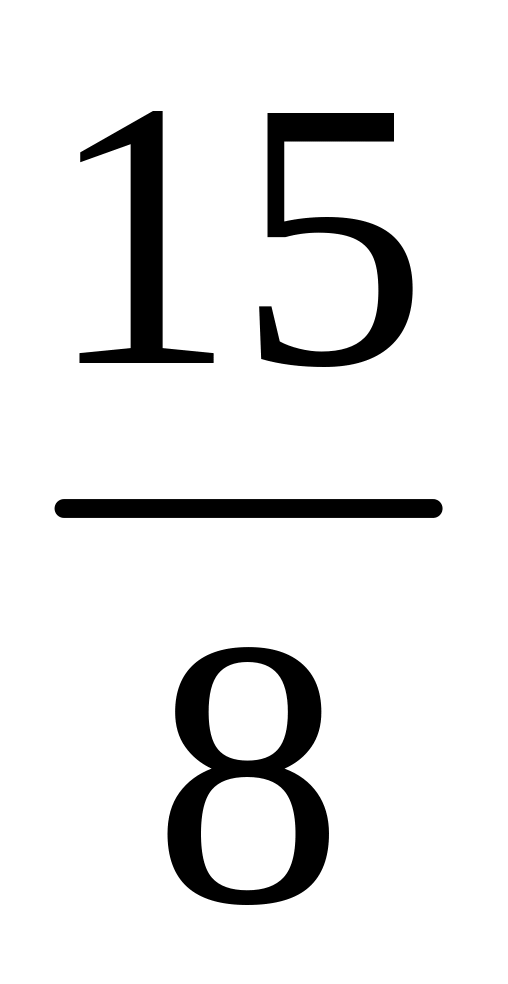 cos2x-
cos2x-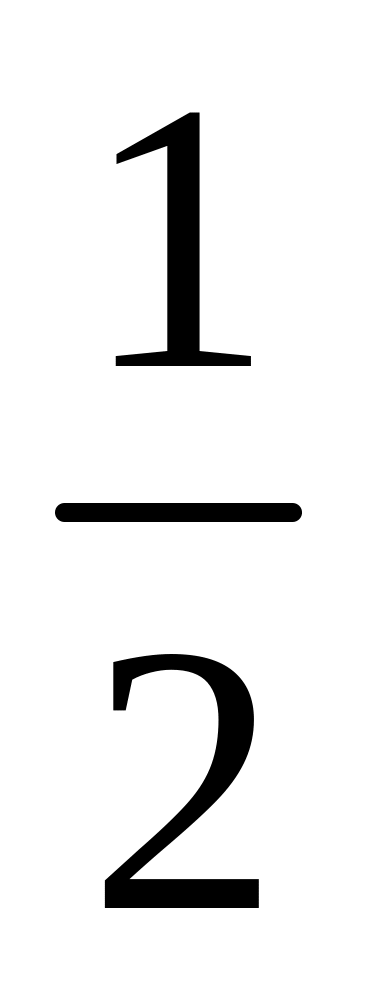 ; (Answers:
±p/6+pn
; (Answers:
±p/6+pncos2x+2cosx+7=2sin(7/2+x)+4sin2(x/2) (Answers:+2n)
Упражнение 82.
Решите системы уравнений:
 ; (Answers:
; (Answers: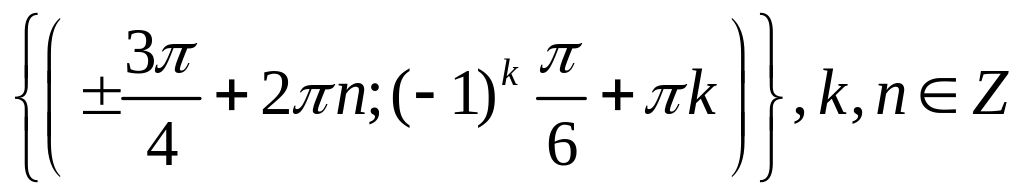 )
)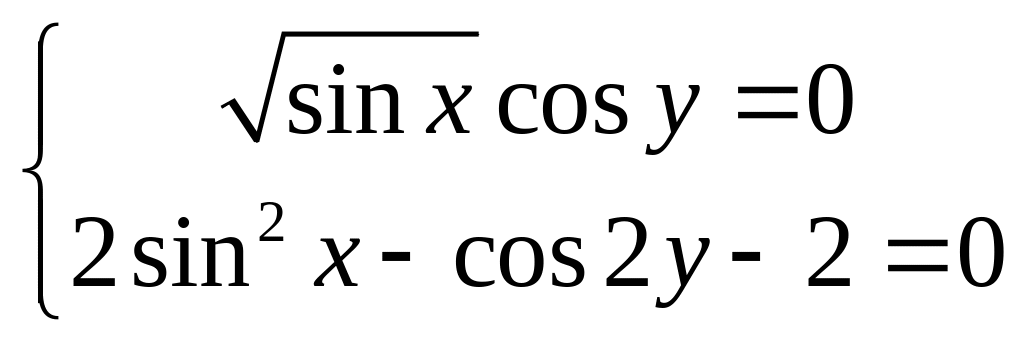 ; (Answers:
; (Answers:
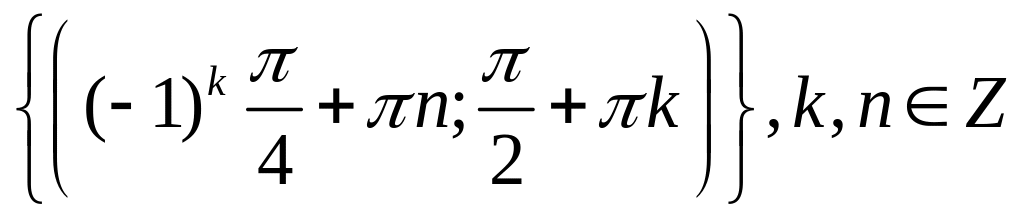
найдите все решения системы
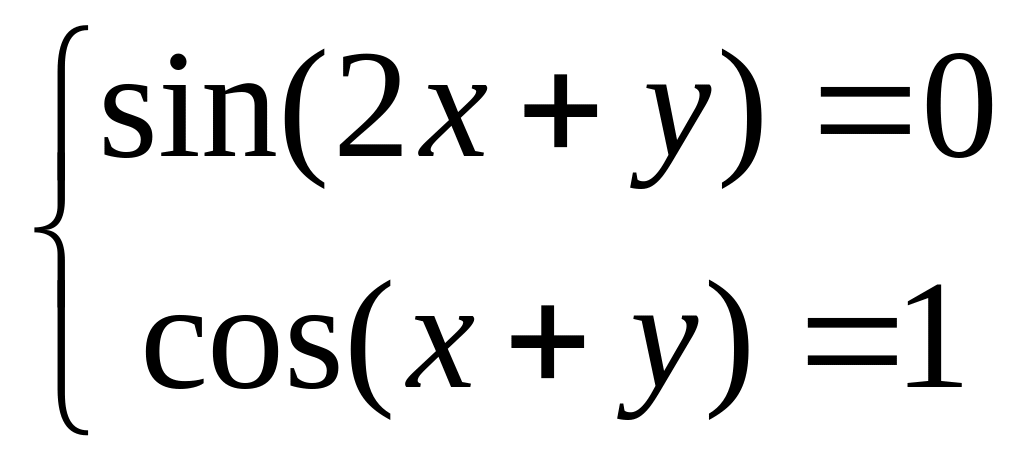 ,
удовлетворяющие условиям
-х,
-2у- (Answers:
{(-;-),(0;-2),(,-)})
,
удовлетворяющие условиям
-х,
-2у- (Answers:
{(-;-),(0;-2),(,-)})
Упражнение 83.
(sin2x−sinx)(2+![]() )
= 0.
)
= 0.
Упражнение 84.
Вычислить
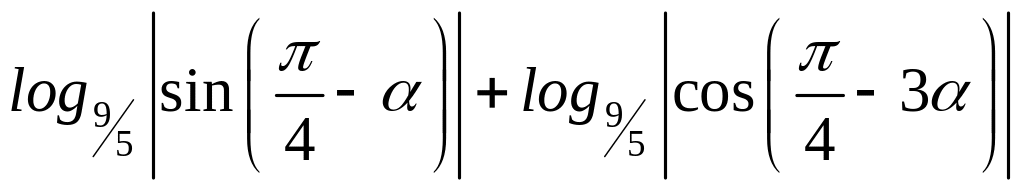 ,
если известно, что sin-cos=
,
если известно, что sin-cos=![]() .
.
Упражнение 85.
Найти все корни уравнения
![]()
(Answers: (-1)n/6)+n)
Упражнение 86.
Найти все значения параметра а, при которых среди корней уравнения
sin2x-2acosx-sinx+a=0 найдутся два, разница между которыми равна /2. (Answers: 1/2, 2/2)
Решите системы уравнений:
Упражнение 87.
![]()
Упражнение 88.
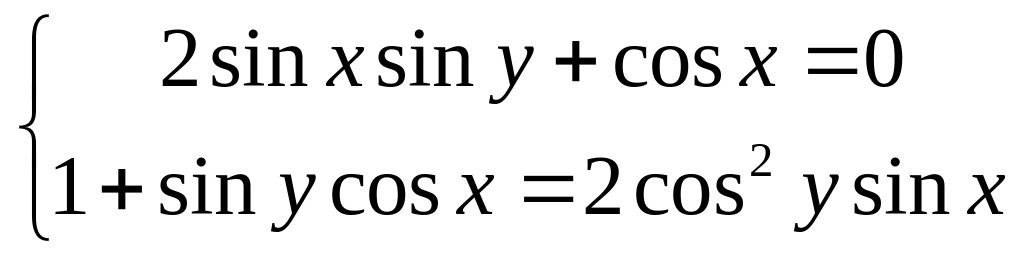
Упражнение 89.
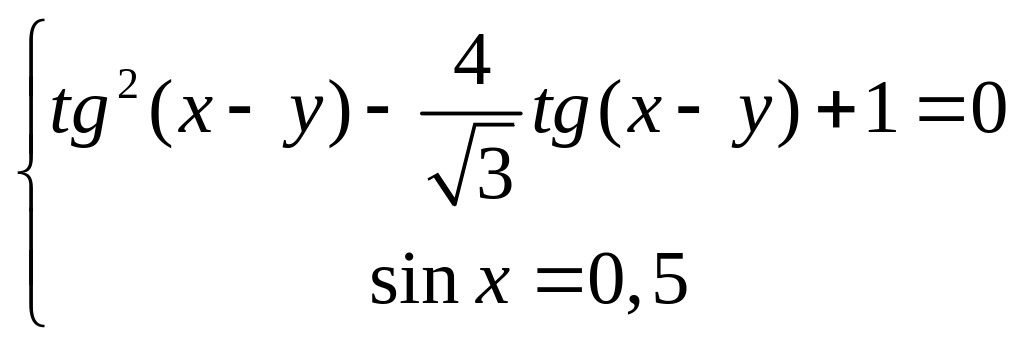
Упражнение 90.
Найдите tgx, если
![]() (Answers:3)
(Answers:3)
Упражнение 91.
При каких значениях х, числа 0, log8(2sin2x), log30,5sin2x в некотором порядке образуют арифметическую последовательность? (Answers: arctg0,25+2n)
Упражнение 92.
Найдите минимальное значение выражения cos2x-8cosx. (Answer: -7)
Лирическое отступление о десятичных дробях.
Мы знаем (и умеем доказывать), что любая обыкновенная дробь эквивалентна конечной десятичной дроби, если её знаменатель содержит лишь степени двойки и пятёрки или бесконечной периодической дроби, если он содержит ещё иные простые делители.
А как понимать выражение вида 34,501002000300004….?
Рассмотрим бесконечную последовательность рациональных чисел:
34; 34,5; 34,501; 34,501002; 34,5010020003; 34,501002000300004;…
Она ограничена (например, числом 35), монотонно возрастает. По упражнению 28, у неё имеется верхняя грань. Это и есть то вещественное число, которое соответствует данной бесконечной десятичной дроби. Можно сказать, что оно выражается этой дробью.
Обратно, допустим мы ткнули в какую-либо точку х на числовой вещественной прямой. Допустим, что х>0. Рассмотрим [x] – целую часть х, то есть, наибольшее целое число, не превосходящее х. Пусть [x]=n0. Разобьём теперь отрезок [n0, n0+1] на 10 равных частей и пусть n1 такое из чисел 0,1,2,3,4,5,6,7,8,9, что n0,n1x<n0,n1+0,1.
Пусть числа n0, n1,…,nk-1 уже выбраны, и пусть nk – наибольшее целое число такое, что n0+10-1 n1+10-2n2+…+10-knkx.
Рассмотрим множество Е={n0+10-1 n1+…+10-knk}, k=0, 1, 2,…
Тогда х – верхняя грань множества Е. Если не все nk начиная с некоторого номера k=t равны 9 (то есть 9=nt=nt+1=nt+2=…), то десятичное разложение числа х равно n0,n1n2n3n4,…
Если же бесконечная дробь содержит бесконечную последовательность девяток, например, 3,240999…, то её верхняя грань –десятичная дробь (рациональное число).
В приведённом примере ею служит число 3,241.
В расширенной двумя символами + и - системе вещественных чисел выполняются (по определению) следующие правила: х+=+, х-=-, х:+=х:-=0.
Если х>0, то х(+)=+, х(-)=-. Если х<0, то х(+)=-, х(-)=+. xR-<x<+. В расширенной числовой системе каждое множество имеет нижнюю и верхнюю грань.
|
Julius Wilhelm Richard Dedekind (6 октября 1831— 12 февраля 1916)
|
|
В 1850 году Дедекинд поступил в университет Георга-Августа в Гёттингене (Гёттингенский университет), ведущий и старейший университет в Нижней Саксонии, слушает курс теории чисел, который читал профессор Мориц Штерн. Карл Фридрих Гаусс, работающий в Гёттингенском университете, к тому времени преподавал начальный курс, и Дедекинд стал его последним студентом. В числе его университетских друзей был Бернхард Риман.
В 1852 году, в возрасте 21 года, Дедекинд получил докторскую степень за работу над диссертацией по теории интегралов Эйлера. В то время Берлинский университет был центром математических исследований, поэтому Дедекинд переехал в Берлин и учился в университете 2 года вместе с Риманом. Затем он вернулся в Гёттинген и в должности приват-доцента преподавал курсы теории вероятности и геометрии.
В 1855 году умер Гаусс, и его кафедру занял Дирихле, общение с которым оказало огромное влияние на Дедекинда. Позже Дедекинд писал, что Дирихле сделал его «новым человеком». До конца жизни Дирихле (1859) они работали вместе и стали близкими друзьями.
Первое время Дедекинд изучал эллиптические и абелевы функции. Кроме того, он был первым в Гёттингене, кто преподавал теорию Галуа и ввёл в широкое употребление предложенное Галуа понятие поля.
В 1858 году Дедекинд начал преподавать в Техническом университете в Цюрихе. В 1859 году вместе с Риманом совершил поездку в Берлин, где встречался с Вейерштрассом, Куммером и другими видными математиками берлинской школы.
Когда в 1862 году Collegium Carolinum был преобразован в Технический институт, известный сейчас как «Технический университет Брауншвейга» (Technische Universität Braunschweig), Дедекинд возвращается в родной Брауншвейг, где проводит остаток своей жизни, преподавая в этом институте. В 1894 году он ушёл на заслуженный отдых, но продолжал иногда читать лекции и публиковаться.
Дедекинд избирался членом Берлинской (1880), Римской и Французской (1900) Академий наук. Он получил докторские степени в университетах Осло, Цюриха и Брауншвейга.

