7

ELECTRICAL CONDUCTIVITY OF FULLY IONIZED PLASMA

7.1Kinetic equations and the results of asymptotic theories

Following the review by Gryaznov et al. (1980), we shall briefly dwell on the basic approaches to the calculation of kinetic coe cients for weakly nonideal plasma. The starting point of the kinetic theory is Liouville’s equation for the N – particle distribution function describing the time evolution of the ensemble of N particles obeying Hamilton’s equations. Integration over coordinates and particle momenta leads to the Bogoliubov, Born, Green, Kirkwood, Yvon (BBGKY) hierarchy of equations.

The BBGKY hierarchy of equations is a set of integro–di erential equations for s–particle distribution functions, each containing in the right–hand side a function of (s + 1)th order. For uncoupling this hierarchy, use is made of an approximation which ignores triple correlations and, in addition, includes the plasma polarization indicative of the fact of charge interaction with a large number of neighbors. This leads to the kinetic equation for the distribution function (Klimontovich 1982, 1999):

∂f1(p1)

∂I(p1)

= −

,

∂t

∂p1

∞ dω

V 2

(k)k2δ(kv1

ω)δ(kv2

ω)

I(p1) = π −∞

−

−

×

2π

∂v11

|ε(k, ω)|2

(7.1)

× f (v2)

− f (v1) ∂v22

(2π)3 .

∂f (v )

∂f (v )

dk

The dielectric permeability of the plasma has the form (Lifshitz and Pitaevskii 1981)

ε(k, ω) = 1 +		4πe2					dpα		∂f		(7.2)
			α					k		,
	α	k2			ω	−	kvα + iδ		∂pα

were δ = +0 and V (k) = 4e2/k2 is the Coulomb potential in the Fourier represen-

tation. For fast processes (ω ωpe = 4πe2ne/m) the dielectric permeability is ε(k, ω) = 1. In this case the screening does not have enough time to evolve and the collision integral has the form proposed by Landau. This expression diverges at large and small distances. For slow processes (ω ωpe), static screening is realized, ε(k, ω) = 1 + (kD/k)2, where kD = rD−1. This eliminates divergence at

276

KINETIC EQUATIONS AND THE RESULTS OF ASYMPTOTIC THEORIES 277

large distances. In order to eliminate divergence at small distances, the collision integral was represented (Hubbard 1961a, 1961b) as a combination of Boltzmann, IB (infrequent “strong” collisions), Landau, IL, and Lenard–Balescu, ILB integrals:

I = IB − IL + ILB.

(7.3)

This corresponds, in fact, to the inclusion of dynamic polarization of the plasma in the Boltzmann collision integral.

Along with the approaches based on the BBGKY hierarchy of equations, the method of time Green functions is employed to write the kinetic equations for the plasma. The emerging kinetic equations are written for advanced and retarded Green functions defining the particle density and the probability of allowed states with pre–assigned momentum and energy. It is by using this method equipped with the diagram technique for classification and regrouping of terms in the series of perturbation theory (ring and ladder fragments are included) that Gould and DeWitt (1967) obtained a convergent equation including the interparticle interaction via the screened Coulomb potential. The emerging approximation is, in a sense, analogous the combination (7.3).

The inclusion of collective e ects in the Coulomb interaction was performed on to the basis of the Fokker–Planck equation, with the collision integral incorporating all moments of the distribution function. In such a procedure, the contribution made by close collisions is described by Boltzmann’s integral and that made by distant collisions is described by the Lenard–Balescu integral with cuto of the contributions from small and large distances.

In order to discuss concrete results, we shall write the expression for electrical conductivity in the form

σ = e2ne/mνi,

		π3/2			Ze2	2
	νi =					nivTe γE−1 ln Λ,	(7.4)
		4√
					kT
			2

where, in the roughest approximation, ln Λ = ln(bmax/bmin). The maximum impact parameter bmax is provided by the screening length. The minimum impact

parameter is the maximum of the two lengths, namely, the classical distance of

√

closest approach, e2/kT , and the thermal electron wavelength, λ = / 2mkT . Spitzer’s formula (6.8), derived for a classical nondegenerate plasma, is only

logarithmically correct. Spitzer’s Coulomb logarithm,

ln ΛSp = ln(3/Γ), Γ = e2/rDkT, rD = kT /8πe2ne,

may serve as the starting point for further refinement.

The result of Williams and DeWitt (1969), who used the collision integral (7.3), corresponds to the Coulomb logarithm with numerical correction,

ln Λ = ln (1/Γ) − 2C + ln 2, C = 0.577.

(7.5)

278 ELECTRICAL CONDUCTIVITY OF FULLY IONIZED PLASMA

Similar result can be obtained from the binary collision approximation assuming a Debye–H¨uckel interaction potential. In the limit Γ 1, Libo (1959) obtained

ln Λ = ln (1/Γ) − 21 − C + ln 2.

The subsequent correction is analogous to the relaxation correction to the ion mobility in solutions of strong electrolytes (Lifshitz and Pitaevskii 1981). The external electric field a ects the correlation functions leading to a spatial deformation of the screening cloud. This reduces somewhat the coe cient of electrical conductivity, because the electric field acting on a particle is compensated to some extent (Kadomtsev 1957, Ebeling and R¨opke 1979). As a result, R¨opke (1988) derived

ln Λ = ln γ−3/2 + 1.102 + √		+ √		−1	γ3/2 ln γ−3/2 + ,
	6		3

where γ = e2(4πne/3)1/3(kT )−1 (Γ2 = 3γ3). The range of validity is limited by the inequalities γ 1 and γ2θ−1 ln Λ , where θ = kT /EF.

The calculation of the coe cient of electrical conductivity for a quantum nondegenerate plasma, using the Lennard–Balescu collision integral, leads to the expression

∞ dq Sii(q)				exp −	2q2	.
ln Λ = 0							(7.6)
	q		|ε(q)|2		8mkT

The use of Debye–H¨uckel static expressions for Sii(q) and ε(q) (5.6) leads to the series whose first terms are (Kivelson and Du Bois 1964)

∞	q3dq
ln Λ = 0		exp	−η2q2/4! = ln η−1 − (C − ln 2) /2, (7.7)
	(q2 + 2)(q2 + 1)

where η = λ/rD. The subsequent terms of this series are given in Ichimaru and Tanaka (1985).

It is not only that the resultant expressions (7.5) and (7.7) are logarithmically exact, but their extralogarithmic terms are exact as well. For a classical ideal plasma (kT Ry), Eq. (7.5) is valid, and for a quantum plasma, Eq. (7.7) is valid. The solution derived by Williams and DeWitt (1969) joins expressions (7.5) and (7.7),

ln Λ = ln η−1 − 2C + ln 2 − 12 exp(z)Ei(z),

where Ei(z) = ∞ dtt−1 exp(−t) and z = exp(2C)(e2/2λkT ). The high–tempera-

z

ture limit corresponds to the limit when z 1, and the low–temperature limit corresponds to that with z 1. Later on, the result of Gould and DeWitt (1967) and Williams and DeWitt (1969) was improved by Rogers et al. (1981).

ELECTRICAL CONDUCTIVITY MEASUREMENT RESULTS

279

102

cm
ohm	10

5

10

15

T 103 K

Fig. 7.1. Electrical conductivity of argon plasma at p = 1 atm (Khomkin 1974). Symbols correspond to the measurement results by Kopainsky (1971) – ; Bues et al. (1967) – ; Hackmann and Ulenbush (1971) – ◦. Solid line corresponds to the calculation by Devoto (1973); dashed line shows the result from the Spitzer formula; symbols + are calculated using the expression (6.12).

7.2Electrical conductivity measurement results

The electrical conductivity is the most revealing and readily observed characteristic of a plasma which governs the dissipative heating of the latter and its interaction with the electromagnetic field. Experimenters are further attracted by the relative simplicity of the well developed registration techniques, as well as by the possibility of performing electrophysical measurements under most diverse experimental conditions.

In the early experiments reviewed by Asinovsky et al. (1971), the attained nonideality parameters did not exceed Γ ≈ 0.2–0.3. Nevertheless, even at these relatively small values of Γ, slight but systematic divergences of the measured and calculated values were observed. The results of a series of investigations of the electrical conductivity of a plasma of inert gases, mainly, in a plasma of arc discharges with plasma density in the range of 1016–1018 cm−3 and temperature on the order of 104 K, demonstrated appreciable deviations of electrical conductivity from the Spitzer values. It has turned out that for the bulk of experimental data the agreement with calculation results is attained if one allows in the calculations for the fact that the plasma is not fully ionized and that collisions with atoms may appreciably reduce the electrical conductivity. Presented in Figs. 7.1 and 7.2 are the results of measurements of the electrical conductivity for argon plasma and the calculation results by Devoto (1973).

However, at somewhat larger Γ, the inclusion of electron collisions did not eliminate the di erence between measured and calculated values of electrical conductivity. The typical experimental conditions (Popovic et al. 1974; Bakeev and Rovinskii 1970; Popovic et al. 1990; G¨unther et al. 1983) corresponded to

280 ELECTRICAL CONDUCTIVITY OF FULLY IONIZED PLASMA

ohm cm

K

0.1 MPa

Fig. 7.2. Electrical conductivity of argon plasma as a function of pressure at di erent temperatures. Measurement results marked by dots: ◦ – Kopainsky (1971); • – Bauder et al. (1973); + – Goldbach et al. (1978). Calculations by Devoto (1973) are shown by solid lines.

pressures in the discharge, p = 1–2 MPa, and temperature T = (1–1.8)·104 K (Fig. 7.3). The inclusion of collisions with atoms (curve 2) leads to agreement between theory and experiment in the low–temperature range. One can see, however, that an increase of temperature causes an appreciable deviation. Curve 3 is plotted with due regard for collision complexes and agrees well with the experimental data. The model of Vorob’ev and Khomkin (1977) introduced new quasiparticle states into the classification of electron–ion interactions, namely, quasibound states and collision complexes. They show up under conditions when Γ is close to unity, and enable one to describe the observed decrease of the coefficient of electrical conductivity. Fortov and Iakubov (1989) outlined this theory, and Khomkin (1978) discussed the role played by electron–atom collisions. An analogous situation is observed in xenon plasma, see Fig. 7.4.

The dynamic methods discussed in Chapters 3 and 9 helped us to perform measurements (Ivanov et al. 1976a; Ebeling et al. 1991; Sechenov et al. 1977; Tkachenko et al. 1976; Fortov et al. 2003) of static electrical conductivity of a plasma in a wide range of nonideality parameters from Γ ≈ 0.3 to the region of extremely high values of Γ, where most of theoretical approximations diverge and the experimental results provide a basis for the construction of physical models of electron transfer in a dense disordered medium. This range has been studied using various media such as cesium, air, neon, argon and xenon.

The high values of plasma density (p of up to 11 GPa, ne up to 1021 cm−3, T of the order of (1–2)·104 K) were obtained by Ivanov et al. (1976a) and Ebeling et al. (1991) for xenon (see Fig. 3.9). In these experiments it was possible to follow the behavior of the electrical conductivity from the states of low density described

ELECTRICAL CONDUCTIVITY MEASUREMENT RESULTS

281

ohm cm

K

Fig. 7.3. Electrical conductivity of argon plasma (Vorob’ev and Khomkin 1977). Experiment: • correspond to Bakeev and Rovinskii (1970); are from Popovic et al. (1990); are from G¨unther et al. (1983). Theory: curve 1 corresponds to Spitzer conductivity; curve 2 is calculated taking into account collisions with atoms; curve 3 accounts for collision complexes.

by the plasma models up to the states obtained by shock compression of liquid xenon in the region of solid–state densities, where the shock compressibility is described by the band theory of solids (Keeler et al. 1965). Figure 7.5 shows the values of “reduced” dimensionless electrical conductivity

√

σ = e2 mσ/(kT )3/2. (7.8)

The resulting combination of experimental data (see Fig. 7.5) definitely points to an underestimation of the measured values of electrical conductivity as compared with Spitzer’s theory. At the same time more stringent theories predict an increase of conductivity with a rise of Γ, as compared with Eq. (7.4).

The existing quantitative divergence between di erent groups of experiments in Fig. 7.5 is due to the physical peculiarities of the high–temperature plasma behavior, as well as to the actual discrepancy of the primary data and to the di culties in determining the Coulomb component of electrical conductivity, i.e., derivation of the frequency νi from the total e ective frequency ν. The latter circumstance is most characteristic of experiments with alkali metals (Sechenov et al. 1977; Barol’skii et al. 1972; Barol’skii et al. 1976) where the contribution by neutrals to the collision frequency is especially large (Pavlov and Kucherenko 1977) in view of a large cross–sections of electron–atom scattering. Thus, at

282 ELECTRICAL CONDUCTIVITY OF FULLY IONIZED PLASMA

, ohm cm

K

Fig. 7.4. The coe cient of electrical conductivity of xenon plasma (Vitel et al. 1990). Symbols are from Popovic et al. (1990); are from Vitel et al. (1990); correspond to Spitzer values.

maximum pressures in the experiment by Ermokhin et al. (1971), the degree of plasma ionization does not exceed 0.1%, thus making it impossible to single out the Coulomb component of σ.

The use of powerful shock waves (Chapter 3) enabled to produce a plasma with high degree of ionization (Ivanov et al. 1976a; Mintsev et al. 1980) for which there was no problem in singling out the Coulomb component. The results obtained using the dynamic methods can be conventionally divided into low– temperature with T ≤ 2 · 104 K (Ivanov et al. 1976a; Ebeling et al. 1991) and high–temperature with T > 2 · 104 K (Ivanov et al. 1976b; Mintsev et al. 1980). The low–temperature points correspond to extremely high densities (up to 4 g cm−3) which are close to the degeneracy limit of the electron component where the strong Coulomb interaction is realized (Γ = 6–10). In the high–temperature region, a plasma emerges with developed single and double ionization (see Section 7.5). As seen in Fig. 7.5 the results obtained for di erent gases (Ar, Xe, Xe, air) agree with each other and enable one to follow the e ect of the Coulomb interaction on the electrical conductivity in a wide and continuously varying range of nonideality parameters, Γ = 0.1–10.

The highest degrees of nonideality are attained as a result of irradiation of the surface of condensed matter by powerful pulses of laser radiation. Speaking of relevant studies, that by Milchberg and Freeman (1990) deserves a special note.

CALCULATIONS OF THE COEFFICIENT OF ELECTRICAL CONDUCTIVITY283

.

.

.

.

.

.

.

.

. . . .

Fig. 7.5. The dimensionless coe cient of electrical conductivity of a plasma σ as a function of the nonideality parameter Γ (Kraeft et al. 1985). The numbered curves correspond to theoretical results: 1 – σSp, 2 – t-matrix, 3 – Born approximation, 4 – expression (7.10). Symbols correspond to experiments: – argon, 11 750 K ≤ T ≤ 159 920 K (G¨unther

et al. 1976); – argon, ◦ – xenon, and	– krypton at T ≈ 25 000 K (G¨unther et al.
1983); – argon, 12 800 K ≤ T ≤ 17 400 K (Bakeev and Rovinskii 1970);		– xenon,

9000 K ≤ T ≤ 13 700 K (Bakeev and Rovinskii 1970); × – cesium, 4000 K ≤ T ≤ 25 000 K (Sechenov et al. 1977; + – hydrogen, 15 400 K ≤ T ≤ 21 500 K (G¨unther et al. 1976);

– air, 13 500 K ≤ T ≤ 18 300 K (Andreev and Gavrilova 1975; Andreev 1975); – polyethylene, 37 000 K ≤ T ≤ 39 000 K (G¨unther et al. 1976).

7.3The results of calculations of the coe cient of electrical conductivity

The asymptotic expressions for ln Λ , given in Section 7.1, are justified only on condition that ln Λ 1 and, when they go into infinity (for example, σSp → ∞ at Γ → 3), they lose their meaning. The simplest convergent value for σ may be derived if, in order to avoid formal divergences, one uses

ln Λ =	1
	2 ln 1 + bmax2 /bmin2 ! ,	(7.9)

where bmax and bmin are the maximum and minimum impact parameters, respectively. Unfortunately, this expression fails to solve the whole problem of constructing an expression for σ, which would turn into correct limiting formulas and describe well the available experimental data.

For this purpose, Gryaznov et al. (1976) proposed a model based on Ziman’s approximation. The derivation is based on the expression for conductivity ob-

284 ELECTRICAL CONDUCTIVITY OF FULLY IONIZED PLASMA

tained in a Lorentz approximation as discussed in Section 6.1 and takes into account ion–ion correlations (see Section 6.3). The resulting expression is

8

e2

∞

−

∂f0

dE.

σ =

3√

0

E2νi(E)−1

(7.10)

m(kT )3/2λ3

∂E

π

Here f0 = {1 + exp[(E − µ)/kT ]}−1

is the electron distribution function and

µ is the chemical potential. The following expression was used for the collision frequency:

/

2 πe4ne νi(E) = π E3/2

qm

0

q3

(q2 + qD2 )2

S(q) dq. (7.11)

Here, ne = (4/√		)(2π 2/m)−3/2			√
						Ef0(E) dE and the quantity qm = 2E/e2
	π
ensures for Eq. (7.10), with an			accuracy to electron–electron interaction, Spitzer’s

asymptote for electrical conductivity. Limiting ourselves to a Debye approximation for the ion–ion correlation function

		g(r) = 1 − (e2/rkT ) exp(−qDr),						(7.12)
and substituting it in the expression for the structure factor, we get
	1	ln(1 + α) −	α		α2
ln Λ =				−		,	α = (qmrD)2.	(7.13)
	2		α + 1		2(α + 1)2

In the limit of weakly nonideal plasma (α 1), this expression reduces to the regular Coulomb logarithm. For strongly nonideal plasma (α 1), the expression for electrical conductivity (7.13) proves finite and contains no nonphysical divergences while reasonably describing experiments (cf. Fig. 7.5).

Apparently, the most systematic approach to constructing interpolation expressions is based on approximation (7.3). It consists in using the unscreened t-matrix approximation, subtraction of the unscreened Born approximation and addition of the Born approximation with dynamic screening. In addition, the electron–atom collisions and electron–electron interactions must be included. The result of such treatment would adequately describe exact limiting expressions. Kraeft et al. (1985) presented the results of extended studies and gave the results of calculations in a wide range of conditions.

H¨ohne et al. (1984) calculated the coe cient of electrical conductivity in a second Born approximation with dynamic screening (see Fig. 7.6). At low density, in order to make an e ective transition to a t–matrix approximation, the thermal wavelength has been replaced (at the place where it acts as the cuto length) by the Landau length. At low and high density, σ has the Lorentz and Ziman asymptotics, respectively. The equation of ionization equilibrium, whose solution gave the electron number density, describes ionization by pressure. The broken curve corresponds to Mott’s transition which, in the approximation used, occurred in a jump rather than continuously. A minimum of the coe cient of

Fig. 7.6.

CALCULATIONS OF THE COEFFICIENT OF ELECTRICAL CONDUCTIVITY285

( ohm cm )

. .

.

.

.

cm

The coe cient of electrical conductivity σ of hydrogen plasma as a function of electon concentration ne for di erent values of temperature T (in units of 104 K) (H¨ohne et al. 1984). The vertical dashed lines indicate Mott’s transition.

electrical conductivity (whose value is a ected by the electron–atom scattering) occurs in the region of Mott’s transition.

Ziman’s formula may be derived from Eqs. (7.10) and (7.11), with due regard for the fact that, under conditions of strong degeneracy, df0/dE = δ(E − EF), and the maximum transferred momentum is equal to 2 kF . Then,

	3/2			ln Λ = 0	2kF	2	S(q)q3 dq,
σZ = π√2Ze2F√m ln Λ ,					+V (q)/4πZe2,
ε

where V (q) is the Fourier component of the potential, and EF = 2kF2 /(2m). The importance of electron–electron interactions is a maximum under con-

ditions of low number density of charged particles, when it is defined by the Spitzer factor γE. It decreases as the nonideality increases, and is suppressed in the case of strong degeneracy due to Pauli’s principle (Schlanges et al. 1984) (see Fig. 7.7).

In Fig. 7.5, the experimental data are compared with the results of calculations in a statically screened t–matrix approximation (curve 2) and statically screened Born approximation (curve 3). At small values of Γ, curve 2 tends to the Spitzer result (curve 1).

The calculations performed by Kraeft et al. (1985) may be classed as widerange calculations of the coe cient of electrical conductivity. Such methods were

286 ELECTRICAL CONDUCTIVITY OF FULLY IONIZED PLASMA

ohm cm

.

cm

Fig. 7.7. The coe cient of electrical conductivity σ of hydrogen plasma, calculated in view

(1) of and disregarding (2) the electron–electron interactions (Schlanges et al. 1984).

called into being by application requirements. Under conditions of a large pulsed energy contribution, the matter may pass through the entire range of nonideality parameters. Ichimaru and Tanaka (1985) tabulated the Coulomb logarithm, given by expression (7.6), in a very wide range of parameters. In a plasma with arbitrary degree of degeneracy, the exchange–correlation correction with Lindhardt’s dielectric permeability was included, and the value of the structure factor was borrowed from the solution of hypernetted–chain equations (see Section 5.1). The nonideality parameter is γ = (Ze2/kT )(4πni/3)1/3 ≤ 2.

Lee and More (1984) performed calculations with reference to the conditions realized during laser–induced thermonuclear fusion. Simple calculations, in which the Coulomb logarithm was provided by expression (7.9), covered a very wide range of conditions (see Fig. 7.8). The screening distance in Lee and More (1984) was provided by the Debye–H¨uckel or Thomas–Fermi radii in the region of weak nonideality, or the mean interionic distance in the range where γ ≥ 1 (see Section 7.4), while in the range where ln Λ turned to be less than two, it was assumed that ln Λ = 2. In the region of Mott’s transition, the coe cient was assumed equal to the minimum Mott value (see Section 4.5), while in the strongly correlated degenerate system an expression of the type of Ziman expression was used for the coe cient of electrical conductivity. Thereby, all of the simplest constructive models were employed.

One can assume that, under conditions of isochoric heating from the melting

CALCULATIONS OF THE COEFFICIENT OF ELECTRICAL CONDUCTIVITY287

keV

g cm

Fig. 7.8. The temperature and density regions treated by Lee and More (1984): Region 1 corresponds to Debye–H¨uckel and Thomas–Fermi screening; in region 2 screening occurs on the average interionic distance; in region 3 it is assumed ln Λ = 2; In region 4 σ = σmin; and region 5 corresponds to Ziman’s region.

point to 100 eV, the matter will pass through the entire set of nonideal–plasma states from liquid metal to ideal plasma. Milchberg and Freeman (1990) constructed the isochore of specific resistance ρ (see Fig. 7.9) as a result of treatment of the results of measurements of the coe cient of reflection of radiation from the aluminum surface heated by a powerful laser pulse with intensity I up to 1015 W cm−2. During the period of 400 fs, the matter does not have enough time to expand, and retains the density of solid aluminum. The measured values were compared by Iakubov (1991) with those derived by the methods of a wide–range description of ρ. The e ect of non–Coulomb scattering (see Section 7.5) from the core of complex Al+3 ions proves to be of extreme importance. The resistance of a degenerate plasma is described by the curve 2 accounting for the non–Coulomb scattering from a core of radius Rc = 1.1a0. In the degeneracy region, the ρZ curve is constructed by Ziman’s formula taking into account scattering by Ashcroft’s pseudopotential with the core radius Rc = 1.1a0. In the region of T 19 eV, the free path length proved to be less than the interparticle distance. Here, the Io e–Regel formula is valid (curve IR),

σIR = (nee2/m)rs/v.

(7.14)

In the aggregate, the curves 2, ρIR, and ρZ give a qualitative description of experiments.

288ELECTRICAL CONDUCTIVITY OF FULLY IONIZED PLASMA

µohm cm

				F		W cm
						eV
. . .

. . . .

k k

Fig. 7.9. The measurements by Milchberg and Freeman (1990) (points) and calculation by Iakubov (1991) (curves) of values of specific resistance ρ for a dense aluminum plasma. Curve 1 corresponds to conversion from the data of Fig. 7.5; curve 2 accounts for non— Coulomb scattering; and curve 3 corresponds to the specific resistance of liquid aluminum.

7.4The coe cient of electrical conductivity of a strongly nonideal “cold plasma”

As the nonideality increases, considerable di culties are encountered in substantiation of the input kinetic equations and methods of solving these equations. In view of the strong collective interaction in a dense plasma, one cannot unambiguously separate the characteristic times of elementary processes, and the time evolution of the system under the e ect of an external field, generally speaking, is no longer described by the Markovian process. The inclusion of bound states in a partly ionized plasma presents a special problem (Klimontovich 1982) because of the absence of appropriate kinetic equations. The results of qualitative analysis point to the possibility of the emergence, under conditions of nonideality, of new types of quasiparticle states. Their description is given below, largely in accordance with Likal’ter (1987, 1992) and Vorob’ev (1987). For γ > 1, the regions of

ELECTRICAL CONDUCTIVITY OF A NONIDEAL “COLD PLASMA” 289

Fig. 7.10. The density of electron states: 1, density of states in a nonideal plasma; 2,

density of states of an isolated atom; 3, density of states of free electrons.

electron interaction with di erent ions overlap, because e2/kT > rs. An electron is permanently in the state of collision, making a transition from the field of one ion to that of another ion. The trajectory of an electron with E > 0 (and e2/E > rs) consists of segments of conjugate hyperbolas, and the trajectory of an electron with E < 0 consists of conjugate segments of ellipses (e2/|E| > rs). Of course, no significant di erences are observed between the trajectories of these two types.

In view of the foregoing, it is obvious that the electron density of states ρ(E) must vary relatively little for low energy values, when |E| ≤ e2/rs, and correspond qualitatively to curve 1 in Fig. 7.10. For high energy values, when E γT , the density of states is close to (6.22). For negative energy of high absolute values, when |E| γT , ρ(E) reaches the asymptotic of quasiclassical density of states for a hydrogen–like atom, ρ(E) = niRy3/2Z3/|E|5/2. The estimation of ρ(E) in the vicinity of zero energy may be performed with the aid of formula (6.25), if one uses the distribution of potential energy of the electron in the field of the nearest ion,

∞		π			Ze2
P (U ) = 4πni 0	R2dR exp −	4	niR3	δ U +		.	(7.15)
		3			R

Indeed, the probability of finding the nearest ion at the distance R from the electron, F (R) = 4πni exp[−4πniR3/3], decreases exponentially at R > rs. We use Eq. (7.15) to derive from Eq. (6.25)

ρ(E) = 2π	2(2h3	Γ(5/6)		2	s	1 + 2Zes2			Γ(5/6)	.	(7.16)
	m)3/2		Ze2/r				Er		Γ(7/6)

Therefore, for low values of energy, the density of states is weakly dependent on energy.

290 ELECTRICAL CONDUCTIVITY OF FULLY IONIZED PLASMA

The situation proves to be close to that discussed in Section 6.4 for the case of weakly ionized dense plasma. As in the latter case, the importance of the energy EP at which the classically accessible regions of motion for negativeenergy electrons overlap for the first time increases. The criterion of overlapping of randomly arranged spheres of radius R at concentration ni has the form 1 − exp(−4πniR3/3) = 0.29 (Shklovskii and Efros 1984). This gives the level of percolation energy

EP = −e2/(0.7rs).

(7.17)

Electrons with E > EP, as well as free electrons, are conduction electrons. However, even if the energy, though exceeding EP, is close to it, these electrons do not yet possess all characteristics of free electrons. Their mobility proves to be smaller.

Let us write the known relation

	σ = e2ne D(E) /kT.
The mean coe cient of electron di usion is
D(E) =	∞ dEρ(E) exp(−E/kT )H(E)D˜ (E)
	2

(7.18)

∞ dEρ(E) exp(−E/kT ) .

EP EP

˜

Here, D(E) is the di usion coe cient for free electrons, and H(E) takes into account the di erence of the electronic di usion coe cient in the vicinity of the

˜

percolation threshold D(E) from D(E). The function H(E) may be determined accurately with the aid of the e ective medium theory (Sarychev 1985). This function, however, has evident properties as well. It is zero at the point E = EP, and it increases with E to unity when E ≥ 0 is reached.

Under conditions of strong nonideality, in view of the properties of H(E), we derive

D(E) = D˜ (EP)	dH	E=EP kT ≈ D˜	(EP)	kT		(7.19)
	dE			EP .

˜ ≈

In order to calculate the di usion coe cient D(EP) v(EP)rs, one must know the mean velocity of an electron with energy close to EP. It is believed that, during transition from one potential well to another, most of the time is spent by the electron in passing through the saddle point. In the saddle point region, the kinetic energy of the electron is not high, of the order of T (there is no other

˜

energy scale). Then, D(EP) = vTe rs. Substituting the written-out quantities in (7.18) we finally derive the following expression for the coe cient of electrical conductivity (accurate to a numerical factor):

σ ωp/√			(7.20)
	γ,

where ωp = 4πnee2/m is the plasma frequency, and ne is the number density of conduction electrons, i.e., electrons with energy E > EP.

ELECTRICAL CONDUCTIVITY OF HIGH–TEMPERATURE PLASMA 291

The question of the coe cient of electrical conductivity for such a system may hardly be regarded as closed, although it is evident that σ is proportional to ωP, because there is no other relevant parameter. If one assumes that an electron, on the contrary, passes through the saddle point very quickly, then v(EP) ≈

EP/m. In this case σ ωp. This expression was proposed by Kurilenkov and Valuev (1984) on entirely di erent model grounds.

7.5Electrical conductivity of high–temperature nonideal plasma. The ion core e ect

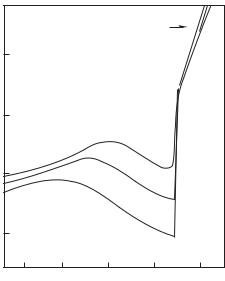
Nonideal plasma experiments are characterized by relatively low (T < 3 · 104 K) temperatures because these experiments are directed toward attaining developed Coulomb nonideality decreasing with a temperature rise. The use of cumulative shock tubes and the e ects of shock wave reflection from obstacles (Mintsev et al. 1980) enables one to advance into the region of extremely high temperatures and obtain a highly heated, multiply ionized plasma with developed Coulomb nonideality of the order of Γ 1–5 (Fig. 7.11). The electrophysical properties of such a plasma turned out to be unexpected to some extent (Ivanov et al. 1976b; Mintsev et al. 1980) because they point to the nonexistence of similarity: the dimensionless electrical conductivity of high–temperature plasma turns out to be smaller than that of low–temperature plasma at the same values of the Coulomb nonideality parameter Γ. Figure 7.12 shows the quantity

				1/2				σ
	= 1 + Z!−				γE−1	Z!			Γ	(7.21)
σ
								ωp

as a function of the nonideality parameter Γ = Ze2/kT rD, where Z is the averaged ion charge, and rD−2 = 4πe2(1 + Z)ne/kT . The experimental data at low and high temperatures clearly separate.

Indeed, in view of the long–range character of the Coulomb potential, the dominant contribution to the transport coe cient at moderate temperatures is made by electron scattering with large impact parameters, thus justifying the use of semiqualitative inclusion of close collisions by introducing various forced cuto s. As the temperature rises, the amplitude of Coulomb scattering, Ze2/kT turns out to be comparable with the proper size of ions, ri, so that the high–energy conduction electrons on their scattering may approach rather closely the nucleus where the interaction potential is no longer purely Coulomb and appears distorted by inner electron shells. The estimates made for rarefied plasma (Ebeling et al. 1991; Maev 1970) indicate that this e ect starts to show against the background of Coulomb scattering only at extremely high temperatures of the order of 2 · 106 K. An increase of the plasma density causes a strengthening of screening of the Coulomb interaction and, consequently, an increase of the importance of close collisions in the plasma which, in its turn, makes possible the manifestation of the e ect of non–Coulomb scattering of electrons with small impact parameters in the region of lower temperatures accessible for experiment, T ≥ 5 · 104 K.

292 ELECTRICAL CONDUCTIVITY OF FULLY IONIZED PLASMA

ohm cm

km s−1

Fig. 7.11. Electrical conductivity σ as a function of shock wave velocity D in xenon at initial pressure p0 = 0.1 MPa. Symbols correspond to experiment: • – Mintsev et al. (1980);

◦ – Ivanov et al. (1976a). Solid curve corresponds to calculation using Eq. (6.8), dashed line accounts for non–Coulomb corrections.

In experiments by Mintsev et al. (1980), characterized by developed ionization (Z = 3) at temperature up to 105 K, use was made of explosion cumulative plasma generators, as well as of linear explosion systems for preparing a highly heated plasma in reflected shock waves. The experiments were performed with xenon gas because the high molecular weight makes the heating of this gas by shock waves e ective, while a large number of bound electrons causes a marked distortion of the Coulomb potential at close distances. The cumulative systems permitted the preparation of a plasma with p ≈ (0.5–3.5) GPa, T ≈ (5 −10) ·104 K, ρ ≈ 0.05–0.5 g cm−3, ne ≈ (0.4–3)·1021 cm−3, Γ ≈ 1.1–2.6, and Z ≈ 2–3. The plasma parameters behind the reflected shock wave amounted to p ≈ (4–8) GPa,

T≈ (3–8)·104 K, ρ ≈ 0.3–2 g cm−3, ne ≈ (2–6)·1021 cm−3, Γ ≈ 2–5, and Z ≈ 2. In the region of low temperatures the obtained data agree well with the

previously obtained results (Fig. 7.5). However, the electrical conductivity of the plasma increases with the shock wave velocity at a much slower rate than one could expect on the basis of conventional plasma models. This points to the absence of similarity of the Coulomb component of the electrical conductivity. The potential of the electron–ion interaction at small distances is stronger than Ze2/r, which leads to an increase of the scattering cross–section as compared with the Coulomb one and, consequently, to a relative decrease of electrical conductivity. The electron–ion interaction can be described by the e ective two– body potential (Maev 1970) allowing for the presence of the ion core,

Fig. 7.12.

ELECTRICAL CONDUCTIVITY OF HIGH–TEMPERATURE PLASMA 293

The reduced coe cient of electrical conductivity σ as a function of the nonideality parameter Γ: Symbols • correspond to experiment in argon, krypton, and xenon at

T ≈ 2.5 · 104 K (Ivanov et al. 1976b); symbols correspond to experiment in xenon at

T ≈ 7 · 104 K (Mintsev et al. 1980). Numbered curves correspond to theoretical calculations: curves 1 and 2 are obtained using pseudopotential (7.22) at the same temperatures; curve 3 shows the Spitzer result σSp.

V (r) =

Zj

(Z − Zj)

exp(

Br)

exp

r

,

B =

1.8Z4/3

,

− r

−

−

(Z − Zj)a0

ei

r

−rD

(7.22) where Z, Zj are the nuclear and ion charges, and rD is the Debye screening distance. At small values of r, the potential (7.22) coincides with the Thomas– Fermi potential and, at r → ∞, it reduces to the Debye–H¨uckel potential. This potential was used in the numerical solution of Schrodinger’s equation for the radial part of the wavefunctions. The phases of scattering δl were determined. The transport cross–sections for electron–ion scattering were then calculated using these scattering phases. The results of these calculations show that for the pseudopotential (7.22) in the region of electrons with the energy of the order of 0.7 a.u. making the main contribution to the electrical conductivity of the plasma at T ≈ 7 · 104 K, the presence of an interaction stronger than (Zje2/r) approximately doubles the scattering cross–sections.

The results of electrical conductivity calculations in accordance with the employed model are shown in Figs. 7.11 and 7.12. It is seen that the ion core model