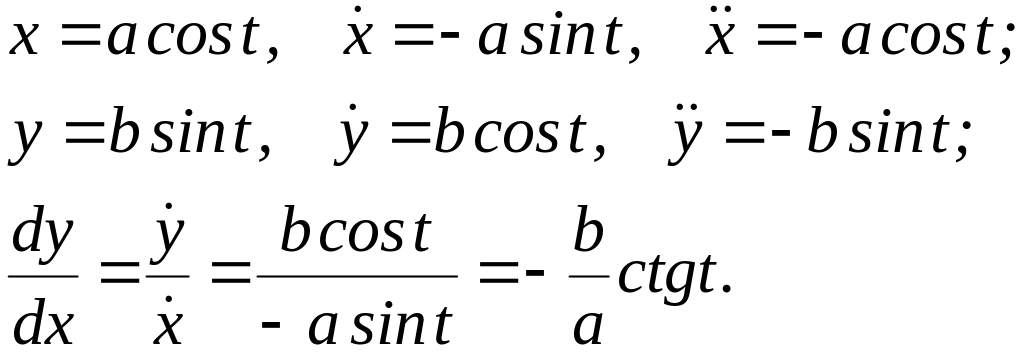- •Предисловие
- •1. Введение в анализ
- •1.1. Основные элементарные функции
- •1.1.1. Некоторые множества вещественных чисел
- •1.1.4. Понятие о функции
- •1.2. Предел последовательности. Бесконечно малые и
- •1.2.1. Предел поcледовательности
- •1.2.2. Ограниченные и неограниченные последователь-
- •1.2.3. Бесконечно малые и бесконечно большие последо-
- •1.2.5. Основные теоремы о пределах
- •1.2.6. Монотонные последовательности
- •1.2.7. Понятие о подпоследовательности числовой по-
- •1.2.8. Необходимое и достаточное условие сходимости
- •1.3. Функция. Предел функции. Непрерывность функции
- •1.3.1. Определение предела функции
- •1.3.2. Теорема (критерий Коши существования предела
- •1.3.3. Непрерывность функции в точке
- •1.3.4. Односторонние пределы
- •1.3.5. Свойства функций, непрерывных в точке
- •1.3.6. Два замечательных предела
- •1.3.7. Эквивалентные бесконечно малые функции и их
- •1.3.8. Монотонные функции. Теорема о существовании
- •1.3.9. Разрывы первого и второго рода
- •2.2. Основные правила и формулы дифференцирования
- •2.3. Дифференциал функции
- •2.4. Производная сложной функции, обратной функции, функции, заданной параметрически
- •Производная обратной функции
- •Производные обратных тригонометрических функций
- •Аналогично
- •2.5 Уравнения касательной и нормали к графику функ-
- •Рассмотрим кривую, уравнение которой .
- •2.6. Производные высшего порядка. Формула Лейбница
- •2.7. Возрастание и убывание функции в окрестности
- •Доказательство:
- •2.8. Поведение функции на отрезке. Теоремы о среднем
- •2.9. Критерии возрастания и убывания функции на ин-
- •2.10. Формула Тейлора Начнем с того, что выведем формулу Тейлора для многочлена
- •Формулы Тейлора для важнейших элементарных функций
- •2.11. Раскрытие неопределенностей. Правило Лопиталя
- •Замечание 1.
- •2.12. Исследование функции одной переменной
- •2.12.1. Отыскание участков монотонности функции
- •2.12.2. Отыскание точек возможного экстремума
- •2.12.3. Выпуклость и вогнутость кривой. Точки перегиба
- •2.12.4. Асимптоты графика функции
- •2.12.5. Общая схема исследования функции и построения ее графика
- •Целесообразно провести следующие исследования:
- •2.13. Наибольшее и наименьшее значение функции, непрерывной на отрезке
- •3. Функции нескольких переменных
- •3.1. Примеры функций нескольких переменных
- •3.2. Определение функции двух переменных. Область определения функции двух переменных
- •3.3. Геометрическое изображение функции двух переменных
- •3.4. Предел и непрерывность функции двух переменных
- •3.5. Частные приращения и частные производные
- •3.6. Полное приращение и полный дифференциал. Использование дифференциала для приближенных вычислений
- •3.7. Сложная функция и ее полная производная
- •3.8. Производная неявно заданной функции
- •3.9. Частные производные высших порядков
- •3.10. Производная по направлению
- •Где и стремятся к нулю, если . Разделим все члены в (3.10.1) на :
- •То , тогда и
- •Аналогично производные и являются производными вдоль положительных направлений координатных осей и .
- •3.11. Градиент
- •3.12. Формула Тейлора для функции двух переменных
- •3.13. Экстремум функции двух переменных
- •3.14. Условный экстремум функции многих переменных
- •Логинов Вениамин Анатольевич
- •Дифференциальное исчисление
- •Курс лекций по дисциплине «Математика» для студентов
- •Инженерных и экономических специальностей мгавт
- •117105, Г. Москва, Новоданиловская нанбережая, строение 2, корп. 1
Производная обратной функции
Теорема.
Если
![]() – строго монотонная непрерывная функция
и
– строго монотонная непрерывная функция
и
![]() – обратная к ней функция, имеющая в
точке у
производную
– обратная к ней функция, имеющая в
точке у
производную
![]() ,
то функция f
имеет в соответст-вующей точке х
производную
,
то функция f
имеет в соответст-вующей точке х
производную
![]() .
.
Доказательство.
 ,
так как функция f(x)
непрерывна, то при
,
так как функция f(x)
непрерывна, то при
![]() и
и
![]() ,
тогда
,
тогда
 .
.
Примеры использования производной от обратной функции
Найти
 .
Мы уже вывели эту формулу. Вывод был
достаточно громоздкий.
.
Мы уже вывели эту формулу. Вывод был
достаточно громоздкий.
Теперь:
если
![]() ,
то
,
то
![]() ,
,
![]() .
.
![]() – результат
тот же самый.
– результат
тот же самый.
Если
а=е,
т.е. у=lnx,
то
![]() .
.
Производные обратных тригонометрических функций
![]() – строго
возрастает на отрезке [1,1].
Напомню график
– строго
возрастает на отрезке [1,1].
Напомню график

Обратная
функция x=siny
имеет производную
![]() ,
если
,
если
![]() .
.
Поэтому
![]()
![]()
Аналогично
![]()
Таким образом, у нас имеется таблица производных основных элементарных функций. Тем самым ясно, как вычислять производные элементарных функций, которые получают из основных элементарных путем конечного числа арифметических операций и взятия функции от функции.
Производная функции, заданной параметрически
Пусть х и у заданы как функции некоторого параметра t:
![]() .
(1)
.
(1)
Каждому значению t соответствуют значения х и у.

Если
рассматривать эти значения x
и y
как координаты точки на плоскости xОy,
то каждому значению t
соответствует определенная точка
плоскости. При изменении t
от
![]() эта
точка описывает на плоскости некоторую
кривую.
эта
точка описывает на плоскости некоторую
кривую.
Уравнения (1) называются параметрическими уравне-ниями этой кривой, t называется параметром, а способ задания кривой (1) –параметрическим.
Предположим,
что функция
![]() имеет обратную,
имеет обратную,
![]() ,
тогда
,
тогда
![]() т.е. у
является сложной функцией от х.
т.е. у
является сложной функцией от х.
По правилу дифференцирования сложной функции
![]() .
Но по правилу дифференцирования обратной
функции
.
Но по правилу дифференцирования обратной
функции
![]() .
.
Эта формула называется формулой дифференцирования функции, заданной параметрически.
Пример:
![]()
![]()
2.5 Уравнения касательной и нормали к графику функ-
ции
Рассмотрим кривую, уравнение которой .

Возьмем
на этой кривой точку М
![]() .
Уравнение любой прямой, проходящей
через эту точку, имеет вид
.
Уравнение любой прямой, проходящей
через эту точку, имеет вид
![]() где k
– ее угловой коэффициент.
где k
– ее угловой коэффициент.
Для
касательной
![]() ,
поэтому уравнение касательной имеет
вид
,
поэтому уравнение касательной имеет
вид
![]() .
.
Прямая, проходящая через точку М перпенди-кулярно касательной, называется нормалью.
Для
нее
![]() .
Поэтому уравнение нормали к графику в
точке М
имеет вид
.
Поэтому уравнение нормали к графику в
точке М
имеет вид
![]() ;
здесь предполагается, что
;
здесь предполагается, что
![]() .
.
2.6. Производные высшего порядка. Формула Лейбница
Если
найдена производная от функции f(x),
т.е. вычислена
![]() – снова функция аргумента х.
Можно еще раз найти производную от
– снова функция аргумента х.
Можно еще раз найти производную от
![]() .
Если эта производная существует, то она
называется второй производной от f(x)
и обозначается через
.
Если эта производная существует, то она
называется второй производной от f(x)
и обозначается через
![]() или
или
![]() .
.
![]() .
.
По
индукции производная n-го
порядка определяется как первая
производная от производной (n–1)
порядка
![]()
![]() .
.
Пример 1.
Пусть
![]() ,
где m
– целое число. Эта функция имеет
производные любого порядка.
,
где m
– целое число. Эта функция имеет
производные любого порядка.

Пусть
 ,
где
произвольное (не целое) число. Тогда
для x>0
эта функция имеет любую производную,
вычисляемую по аналогичной формуле:
,
где
произвольное (не целое) число. Тогда
для x>0
эта функция имеет любую производную,
вычисляемую по аналогичной формуле:
![]()
3.
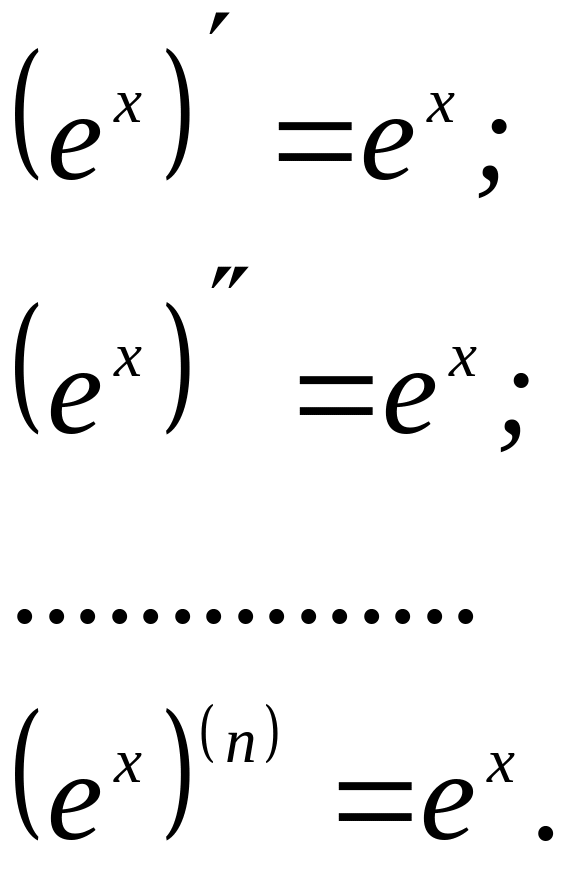
4.

Формула Лейбница
Это формула дает возможность вычислить производную n-го порядка от произведения двух функций u(x)v(x).
Давайте найдем несколько первых производных и установим общий закон, пригодный для вычисления производной любого порядка.

Вспомним бином Ньютона:

Если
в этой формуле заменить
![]() (соответственно считая, что
(соответственно считая, что
![]() ),
то и получим формулу, которая носит
название формулы Лейбница.
),
то и получим формулу, которая носит
название формулы Лейбница.
![]()
Производные различных порядков от неявных функций и функций, заданных параметрически
Сначала покажем способ нахождения производных различного порядка от неявных функций (на примере).
Пусть
![]() – неявная связь у
и х
(у
не выражен явно через х).
– неявная связь у
и х
(у
не выражен явно через х).
Или
![]() (1)
(1)
Дифференцируем по х обе части равенства, имея в виду, что у есть функция х:
![]() .
.
Отсюда:
![]() .
Первая производная найдена, но выражена
она и через х
и через у.
.
Первая производная найдена, но выражена
она и через х
и через у.
Последнее равенство еще раз дифференцируем по х (имея опять в виду, что у=у(х)).

Подставляя
вместо
![]() ее значение (зависящее от х
и у),
найдем
ее значение (зависящее от х
и у),
найдем

Из
(1) заметим, что
![]() ,
так что
,
так что
![]()
Дифференцируя
по х
полученное равенство, найдем
![]() и.т.д.
и.т.д.
Производная второго порядка от функции, заданной параметрически
![]()
Мы знаем формулу для первой производной

Продифференцируем это равенство по х, имея в виду, что t – функция х.
![]()
Пример.