1.2. Предел последовательности. Бесконечно малые и

бесконечно большие последовательности.

Основные теоремы о пределах

1.2.1. Предел поcледовательности

Определение.

Если каждому числу n натурального ряда чисел 1,2, …, n, … ставится в соответствие по определенному закону некоторое действительное число x_n, то множество занумерованных чисел x₁, x₂, …, x_n, … будем называть последовательностью. Числа x_n называются членами или элементами последовательности.

Примеры вам хорошо известны:

1. – арифметическая последовательность;

2. – геометрическая последовательность.

Примеры других последовательностей:

Обычно последовательности обозначают символом и т.д.

Понятие предела последовательности связано с поведением последовательности при

Определение.

Число A называется пределом последовательности найдется такой номер , что для всех натуральных n>N выполняется неравенство

При этом записывают:

Последовательность, имеющую предел, называют сходящейся, в противном случае ее называют расходящейся.

Отметим следующие два обстоятельства:

1. Неравенство 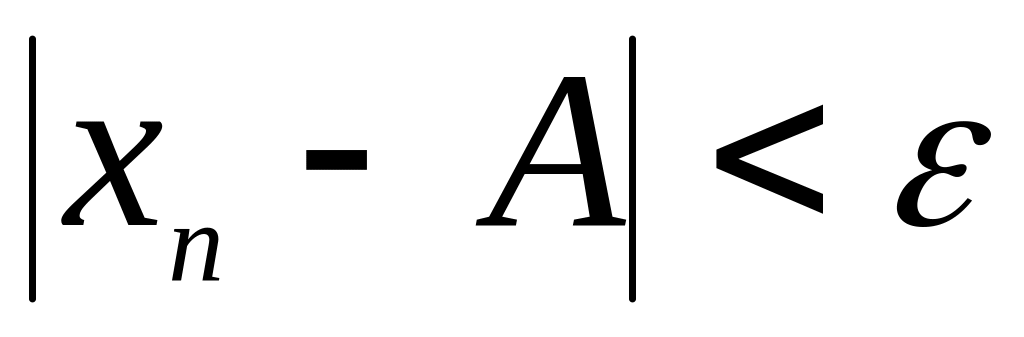означает, что Таким образом, если последовательность сходится, то при любом начиная с некоторого номера все члены последовательности находятся внутри –окрестно-сти точки А;

2. Номер, начиная с которого все члены попадают в , зависит от выбранного значения

Примеры:

1. Рассмотрим последовательность .

Покажем, что число 0 является пределом этой последовательности, т.е. что В соответствии с определением предела это означает, что для любого необходимо найти , так чтобы при n>N , т.е.

Пусть . Тогда все члены, начиная с 101-го будут меньше, чем 0,01. Почему? Потому что при n 101 и т.д. Действительно, все члены, начиная со 101, оказываются меньше, чем 0,01. Как это выглядит геометрически?

В интервал (0; 0,01) попадает бесконечное число членов последовательности, причем ни один из них из этого интервала не выходит.

Пусть Тогда и картина будет такая:

Начиная с номера 1001, все члены последовательности попадают в интервал (0; 0,001).

А если Тогда поступим так: поскольку может оказаться числом не целым, то положим (дробная часть отброшена). Тогда при все члены последовательности находятся в интервале

Таким образом, мы показали, что, выбирая , получаем, что для всех т.е. число 0 является пределом нашей последовательности и мы можем записать:

.

В приведенном примере все члены нашей последовательности оказываются больше, чем предел и стремятся к нему при , приближаясь справа. Но это совсем не обязательно.

2. Пусть т.е. имеем последовательность .

При этом также. Но как ведут себя члены последовательности?

Члены последовательности “сгущаются” около 0, оказываясь попеременно то справа, то слева от предельного значения. Но если взять любую - окрестность точки 0 (а именно это утверждается в определении предела), то для все члены последовательности оказываются в этой - окрестности нуля.

3. Приведу примеры расходящихся последовательностей:

a) ; 1, 2, ….

Ни к какому конечному числу эта последовательность не стремится.

б) 0, 2, 0, 2,0, 2, … .

Казалось бы, в точках 0 и 2 имеются “сгущения”, но в любую - окрестность этих точек все члены, начиная с некоторого номера N, не попадают. Последовательность расходится.

Из приведенных примеров ясно, что можно привести другие определения предела последовательности. Дадим еще два определения.

Определение 2.

Число А называется пределом последовательности найдется такое число N, что все точки x_n с индексами n > N попадают в - окрестность точки A.

Определение 3.

Число А называется пределом последовательности , если вне любой окрестности числа А имеется конечное или пустое множество точек x_n.

Все три определения равноценны.