Функции нескольких переменных

Пусть - некоторое подмножество - мерного пространства: .

Определение. Если в силу некоторого закона каждой точке поставлено в соответствие определенное число 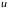, то говорят, что на множестве задана функция

т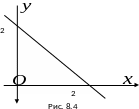 очки -мерного пространства или функция переменных

При этом множество называют множеством (областью) определения функции

В случае 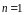данное определение совпадает с определением числовой функции одной переменно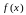й . При 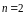вместо 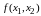будем писать также 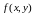, в случае 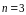вместо 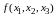- также

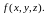
Основной способ задания функций двух и более переменных - аналитический, то есть с помощью формул. Если нет каких-либо дополнительных условий, то областью определения функции 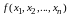считается множество точек , для координат которых формула имеет смысл.

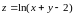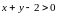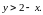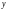П ример. Рассмотрим формулу . Она имеет смысл при или Каждой точке координаты которой удовлетворяют данному условию, формула ставит в соответствие определенное вещественное число , то есть определяет как функцию двух переменных и . Область определения функции есть множество точек плоскости , координаты которых удовлетворяют неравенству 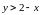. Это все точки плоскости, которые лежат выше прямой 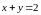(рис. 8.4).

Ф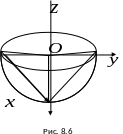 ункция 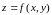двух переменных имеет простую геометрическую интерпретацию. Каждую пару значений переменных и из области определения функции вместе с соответствующим значением можно рассматривать как декартовы координаты некоторой точки 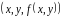трехмерного пространства. Когда точка с координатам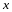и и пробегает все множество определения функции на плоскости 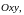соответствующая ей точка в пространстве будет описывать обычно некоторую поверхность. Эта поверхность и будет геометрическим образом (графиком) функции

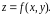
Примеры.

1. Для функции 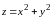область определения - вся плоскость график функции - параболоид вращения (рис.8.5).

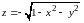2. Функция имеет областью определения круг 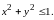Графиком ее является нижняя полусфера с центром в начале координат и радиусом, равным 1 (рис.8.6). Для наглядного геометрического изображения функции трех переменных кроме трех координатных осей переменных 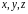потребовалась бы еще четвертая ось для переменной 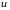, что не может быть осуществлено в пределах трехмерного пространства.

Предел функции нескольких переменных

Рассматривая функцию переменных как функцию точки -мерного пространства, можно дать определение предела функции нескольких переменных аналогично тому, как это было дано для функции одной переменной.

Пусть функция 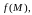где определена в некоторой окрестности конечной или бесконечной точки 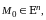причем, если - конечная точка, то в самой этой точке функция может быть и не определена.

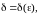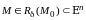
Определение. Если для любого наперед заданного положительного числа можно указать такое положительное число зависящее от что из условия 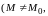если - конечная точка) следует условие 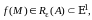то называется пределом функции 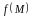в точке (или при , стремящейся к . При этом пишут

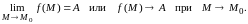
Если 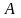- число, то предел функции называется конечным, если же равно 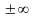или 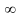, то предел называется бесконечным или несобственным.

Для предела функции нескольких переменных справедливы теоремы, аналогичные по формулировкам и доказательствам, соответствующим теоремам о пределах функции одного аргумента. Ограничимся формулировкой теоремы о конечных пределах.

Теорема. Если при 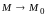функци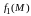и и 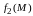стремятся каждая к конечному пределу, то

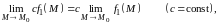
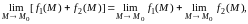
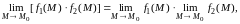
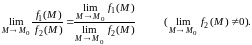
Определение. Функция 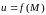называется бесконечно малой в точке (или пр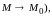и если

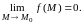
Как и для функции одной переменной, если функция 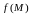имеет в точке конечный предел то ее можно представить в виде

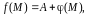
где 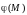- бесконечно малая при

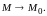
Сравнение бесконечно малых функций нескольких переменных производится так же, как для бесконечно малых функций одной переменной.