
- •Гаврилов в.Л. Функции нескольких переменных
- •Евклидово -мерное пространство
- •Окрестности. Области
- •Функции нескольких переменных
- •Предел функции нескольких переменных
- •Непрерывность функции нескольких переменных
- •Решение задач
- •Вопросы для самопроверки по теме 8.1
- •Тесты для самопроверки по теме 8.1
- •Ответы на тесты по теме 8.1
- •8.2. Дифференцирование функций нескольких переменных
- •Частные производные
- •Дифференцируемость функции нескольких переменных
- •Полный дифференциал
- •Дифференцирование сложной функции одной переменной. Полная производная
- •Дифференцирование сложной функции нескольких переменных. Инвариантность формы полного дифференциала
- •Тогда функция
- •Дифференцирование неявных функций
- •В нашем случае
- •Частные производные высших порядков
- •Полные дифференциалы высших порядков
- •Рассмотрим функцию
- •Аналогично предыдущему можно показать, что
- •Решение задач
Вопросы для самопроверки по теме 8.1
Дайте определение -мерного евклидова пространства.
Дайте определение -окрестности точки. Приведите примеры -окрестности точки на плоскости и в пространстве.
Дайте определение внутренней и граничной точки множества.
Дайте определение открытой и замкнутой области.
Приведите примеры ограниченной замкнутой области на плоскости и в пространстве.
Дайте определение функции
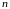 переменных.
переменных.Дайте определение предела функции в точке . Когда предел называется конечным?
Дайте определение непрерывности функции в точке.
Вспомните свойства непрерывных функций одной переменной. Сформулируйте эти свойства для функций нескольких переменных.
Тесты для самопроверки по теме 8.1
Значение функции
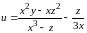 в точке
в точке
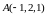 равно
равно
а)
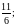 б)
б)
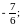 в)
в)
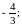 г)
г)
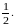
Область задана системой неравенств
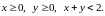 Точка
Точка
 будет для области
будет для области
а) внутренней; б) граничной; в) внешней.
Точка
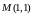 для области определения функции
для области определения функции
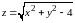 будет
будет
а) внутренней; б) граничной; в) внешней.
Функция
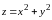 на множестве
на множестве
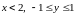
а) ограничена сверху, но не ограничена снизу;
б) ограничена снизу, но не ограничена сверху;
в) ограничена;
г) не ограничена ни сверху, ни снизу.
Функция
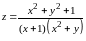
а) непрерывна; б) имеет одну точку разрыва;
в) имеет две точки разрыва; г) имеет линии разрыва.
Ответы на тесты по теме 8.1
1-б; 2-б; 3-в; 4-б; 5-г.
8.2. Дифференцирование функций нескольких переменных
При изучении данной темы Вам предстоит ознакомиться со следующими вопросами:
Частные производные.
Дифференцируемость функций нескольких переменных.
Полный дифференциал.
Дифференцирование сложной функции одной переменной. Полная производная.
Дифференцирование сложной функции нескольких переменных. Инвариантность формы полного дифференциала.
Дифференцирование неявных функций.
Частные производные высших порядков.
Полные дифференциалы высших порядков.
После изучения темы Вам следует ответить на вопросы для самопроверки и решить тест. При возникновениии вопросов следует обратиться к [6], глава 2, с.13-31.
Студентам очно-заочной и заочной форм обучения надо решить две задачи в соответствии со своим вариантом из № 171-180 и 181-190.
Частные производные
Рассмотрим
функцию двух переменных
Будем считать,
что она определена и непрерывна в
некоторой окрестности
точки
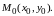 Придадим
аргументу
постоянное
значение
Придадим
аргументу
постоянное
значение
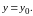 Тогда функция
Тогда функция
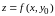 будет функцией одного переменного
будет функцией одного переменного
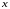 .
Зададим
фиксированному значению
произвольное
приращение
.
Зададим
фиксированному значению
произвольное
приращение
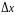 ,
но такое,
чтобы
,
но такое,
чтобы
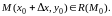 При
этом функция получит приращение
При
этом функция получит приращение
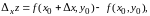
которое называется частным приращением по переменной в точке .
Определение.
Если
при
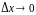 отношение
отношение
 стремится
к конечному или бесконечному пределу,
то этот предел
называется частной
производной функции
по переменной
в точке
стремится
к конечному или бесконечному пределу,
то этот предел
называется частной
производной функции
по переменной
в точке
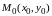 и
обозначается
и
обозначается
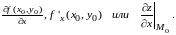
Итак, по определению,
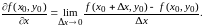
Аналогично определяются и обозначаются частное приращение и частная производная функции по переменной в точке
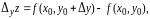
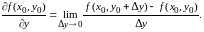
Частные производные называются конечными или бесконечными в зависимости от того, конечен (равен числу) или бесконечен соответствующий предел.
Значение
частной производной зависит от точки
в которой
она вычисляется. Поэтому частная
производная функции
двух переменных
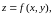 вообще говоря, есть функция точки
то есть является функцией двух переменных
и
.
Частные производные, рассматриваемые
как функции двух переменных,
обозначаются одним из следующих символов:
вообще говоря, есть функция точки
то есть является функцией двух переменных
и
.
Частные производные, рассматриваемые
как функции двух переменных,
обозначаются одним из следующих символов:
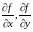 или
или
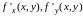 ;
;
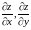 или
или
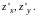
Все, сказанное о частных производных функции двух переменных с надлежащими изменениями, распространяется и на функции любого числа переменных.
Так как при отыскании частных производных функций нескольких переменных все переменные, кроме той, по которой производится дифференцирование, считаются постоянными (фиксированными), то правила и формулы дифференцирования функций одной переменной остаются в силе и при отыскании частных производных функций нескольких переменных.
Пример 1. Найти частные производные функции
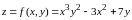 .
.
Решение.
Заданная функция есть функция двух
переменных
и
.
При дифференцировании по
,
то есть при нахождении
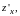 полагаем, что
полагаем, что
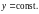 Поэтому
Поэтому

Аналогично
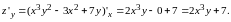
Пример
2. Найти
частную производную функции
 по переменной
по переменной
 в точке
в точке
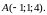
Решение.
При дифференцировании по переменной
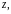 считая
считая
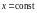 и
и
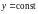 имеем
имеем
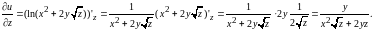
Теперь
находим значение частной производной
в точке

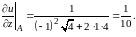
Выясним геометрический смысл частных производных функции двух переменных.
П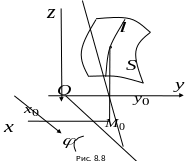 усть
функция
задана в некоторой области
и ее геометрическим образом служит
поверхность
усть
функция
задана в некоторой области
и ее геометрическим образом служит
поверхность
 (рис. 8.8).
(рис. 8.8).
Возьмем
точку
 .
При
.
При
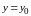 функция
будет функцией одной переменной
функция
будет функцией одной переменной
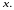 Графиком этой функции будет кривая
Графиком этой функции будет кривая
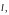 полученная при пересечении поверхности
плоскостью
полученная при пересечении поверхности
плоскостью
Если
при
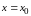 существует касательная к кривой
существует касательная к кривой
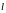 (лежащая в плоскости
(лежащая в плоскости
 ),
то тангенс угла
),
то тангенс угла
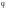 наклона этой касательной (к оси
наклона этой касательной (к оси
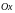 )
и будет численно равен значению
)
и будет численно равен значению
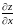 в точке
.
В этом и заключается геометрический
смысл частной производной по переменной
.
в точке
.
В этом и заключается геометрический
смысл частной производной по переменной
.
Аналогично выясняется геометрический смысл частной производной по переменной .
