Дифференцируемость функции нескольких переменных
Пусть
функция
определена в некоторой окрестности
точки
.
Зададим в этой точке произвольные
приращения аргументам
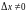и
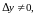но такие, чтобы точка
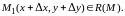При этом функция получит полное приращение
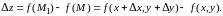
Определение.
Функция
называется
дифференцируемой в точке
если ее полное приращение
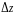можно представить в виде
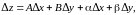(8.7)
где
и
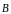не зависят от
и
,
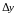а
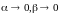при
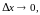
Необходимые условия дифференцируемости функции двух переменных дает следующая теорема.
Теорема. Если функция дифференцируема в точке то в этой точке существуют конечные частные производные по переменным и , причем
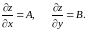(8.8)
Заметим,
что
и
не зависят от
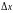и
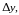но зависят от
и
,
то есть выбора точки
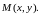
В
случае функции одной переменной
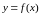представимость приращения функции
в виде суммы
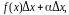где
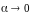при
обеспечивается одним фактом существования
конечной производной
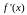в рассматриваемой точке
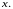Если же мы имеем дело с функцией двух
(или большего числа переменных), то
только существование конечных частных
производных
и
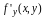функции
уже недостаточно для того, чтобы полное
приращение
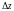можно было представить в точке
в виде (8.7), то есть чтобы функция была
дифференцируема в точке
Достаточные условия дифференцируемости функции двух переменных дает следующая теорема.
Теорема.
Если в точке
функция
обладает непрерывными частными
производными
и
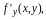то она дифференцируема в этой точке.
Для функции двух (и более) переменных, как и для функции одной переменной, имеет место теорема о непрерывности дифференцируемой функции.
Теорема. Если функция дифференцируема в точке то она непрерывна в этой точке.
Доказательство.
Из (8.7) следует, что
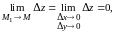а это и означает непрерывность функции
в точке
В заключение отметим, что изложение велось для функции двух переменных только для краткости записей. Все сказанное без существенных изменений распространяется на функции любого конечного числа переменных.
Так,
функция трех переменных
называется дифференцируемой
в
точке
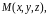если ее полное приращение
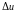можно представить в виде
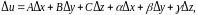(8.9)
где
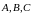не зависят от
,
а
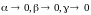при
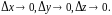
Необходимое условие дифференцируемости в точке функции любого числа переменных – существование конечных частных производных, достаточное – существование непрерывных частных производных в этой точке.
Полный дифференциал
Пусть функция дифференцируема в точке то есть выполняется условие (8.7). С учетом (8.8) полное приращение функции можно записать в виде
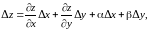(8.10)
где
и
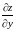- частные производные в точке
и
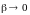при
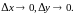
Определение. Если функция дифференцируема в точке то ее полным дифференциалом в этой точке называется выражение
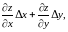
которое
обозначают
или
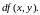
Как
и для функции одной переменной, если
и
независимые переменные, то принимается
по определению, что
и принято записывать
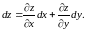(8.11)
Пример.
Найти полный дифференциал функции
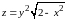в точке
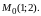
Решение. Найдем сначала выражение для полного дифференциала в точке по формуле (8.11). Так как
то
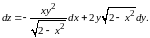
В точке имеем
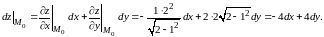
При рассмотрении полного дифференциала необходимо обратить внимание на следующее.
Из определения следует, что полный дифференциал (в дальнейшем - просто дифференциал) представляет собой ту часть приращения функции, которая пропорциональна приращениям аргументов (линейна относительно и
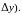
Разность между приращением и дифференциалом функции
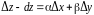(8.12)
есть
бесконечно малая более высокого порядка
малости по сравнению с
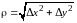(расстоянием между исходной точкой
и смещенной точкой
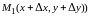при
На основании этого дифференциал называют главной (линейной) частью приращения функции.
Дифференциал
имеет более простую зависимость от
приращения
аргументов по сравнению с приращением
функции и сколь угодно
мало от него отличается при достаточно
малых значениях
.
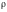Это
дает возможность заменять приращение
функции ее
дифференциалом при приближенных
вычислениях.
Все сказанное о дифференциале функции двух переменных легко обобщается на случай трех и более переменных. Так, например, формула (8.11) для дифференциала функции трех переменных примет вид
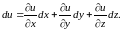(8.13)