
- •Чисельні методи
- •5 Методи розв'язку інтегральних рівнянь
- •1 Пакет pde Tools решения задач для уравнений в частных производных
- •1.2. Выполнение расчетов в пакете matlab
- •1.3 Задачи для самостоятельного решения
- •2 Метод сіток розв'яЗання еліптичних рівнянь
- •2.1 Метод сіток – постановка задачі
- •2.2 Побудова сітки й апроксимація рівняння
- •2.4 Погрішність вирішення й збіжність
- •2.5 Задача для самостійного вирішення на практиці
- •2.6. Завдання до лабораторної роботи
- •3 Метод сіток
- •3.1 Постановка задачі
- •3.2 Явна різницева схема
- •3.3 Неявна різницева схема
- •3.4 Різницеві схеми підвищеної точності. Схема Кранка-Нікольсона
- •3.5 Задачі для самостійного розв'язку на практиці
- •Завдання до лабораторної роботи
- •3.7 Контрольні питання
- •4 Метод сіток розв'язку крайових задач для хвильових рівнянь
- •4.1 Постановка задачі
- •Явна схема
- •4.3 Неявна схема
- •4.4 Задача для самостійного розв'язку на практиці
- •Завдання до лабораторної роботи
- •4.6 Контрольні питання
- •5 Методи розв'язку інтегральних рівнянь
- •5.1 Загальні відомості про інтегральні рівняння
- •5.2 Метод послідовних наближень розв'язку інтегральних рівнянь Фредгольма
- •5.3 Квадратурний метод розв'язку інтегральних рівнянь Фредгольма
- •5.4 Загальні відомості про інтегральні рівняння Вольтерра
- •5.5 Метод послідовних наближень розв'язку інтегральних рівнянь Вольтерра
- •5.6 Квадратурний метод розв'язку інтегральних рівнянь Вольтерра
- •5.7 Завдання до лабораторної роботи
- •5.8 Контрольні питання
- •6 Література
3 Метод сіток
РОЗВ'ЯЗКУ початково-крайових задач
для РІВНЯНЬ ПАРАБОЛІЧНОГО ТИПУ
3.1 Постановка задачі
Розглянемо розв'язок змішаної крайової задачі для диференційних рівнянь з частинними похідними (ДРЧП):
![]() ,
,![]() ,
,
![]() (3.1)
(3.1)
с початковою умовою:
![]() ,
,
![]()
і граничними умовами:
![]() ,
,
![]() ,
.
,
.
Розглянуте
рівняння описує розподіл температури
в стрижні, початкова температура якого
дорівнює значенню функції
![]() .
Температура на лівому кінці стрижня
змінюється за законом
.
Температура на лівому кінці стрижня
змінюється за законом
![]() ,
на правому кінці стрижня відбувається
теплообмін з навколишнім середовищем,
температура якого визначається функцією
,
на правому кінці стрижня відбувається
теплообмін з навколишнім середовищем,
температура якого визначається функцією
![]() .
.
Для розв'язку задачі методом кінцевих різниць побудуємо прямокутну сітку (рис. 3.1), вузли якої визначаються формулами:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Значення
![]() на лівій і нижній сторонах сітки відомі
з початкових і граничних умов. На правій
границі відоме значення частинної
похідної розв'язку рівняння по змінній
.
на лівій і нижній сторонах сітки відомі
з початкових і граничних умов. На правій
границі відоме значення частинної
похідної розв'язку рівняння по змінній
.
Замінимо частинні похідні в рівнянні теплопровідності їх кінцево-різницевими апроксимаціями в кожному внутрішньому вузлі:
![]() ,
(3.2)
,
(3.2)
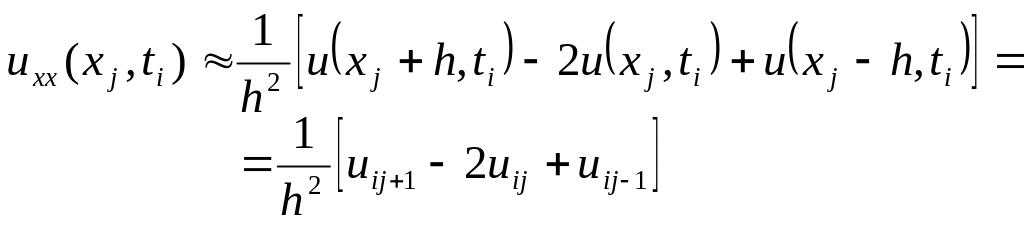 (3.3)
(3.3)
Р исунок
3.1 – Просторово - часова сітка й шаблони,
що використовуються для розв'язку
рівнянь параболічного типу
исунок
3.1 – Просторово - часова сітка й шаблони,
що використовуються для розв'язку
рівнянь параболічного типу
Вираз
(3.2) можна вважати наближенням похідної
як у точці
![]() так і в точці
так і в точці
![]() порядку
порядку
![]() .
.
Вираз
(3.3) апроксимує похідну з порядком
![]() .
Таким чином, порядок апроксимації
диференційного рівняння
.
Таким чином, порядок апроксимації
диференційного рівняння
![]()
Для розв'язку змішаної крайової задачі необхідно апроксимувати похідну в граничній умові на правому кінці:
![]() .
.
Використовуючи кінцево-різницеву апроксимацію, одержуємо:
![]() (3.4).
(3.4).
Порядок
апроксимації останньої формули
![]() .
.
3.2 Явна різницева схема
Підставимо вирази (3.2) і (3.3) у рівняння (3.1) і розв'яжемо його щодо значень функції на верхньому часовому шарі:
![]() .
(3.5)
.
(3.5)
Формула (3.5) вирішує поставлену задачу, оскільки вона виражає розв'язок у цей момент часу через розв'язок у попередній момент часу.
З
(3.4) знаходимо: ![]() .
(3.6)
.
(3.6)
Алгоритм обчислень за явною схемою реалізується наступною послідовністю дій.
Обчислюємо значення сіткової функції на першому часовому шарі з початкових умов:
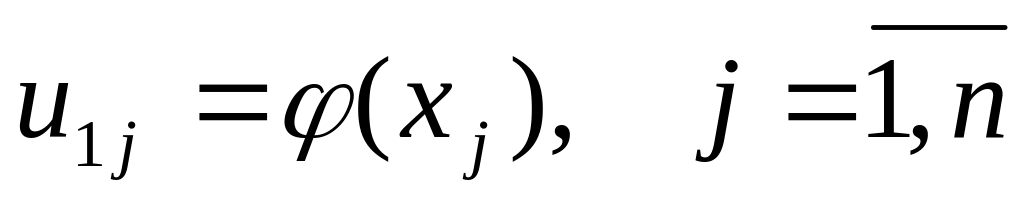 .
.Знаходимо розв'язок на сітковому шарі
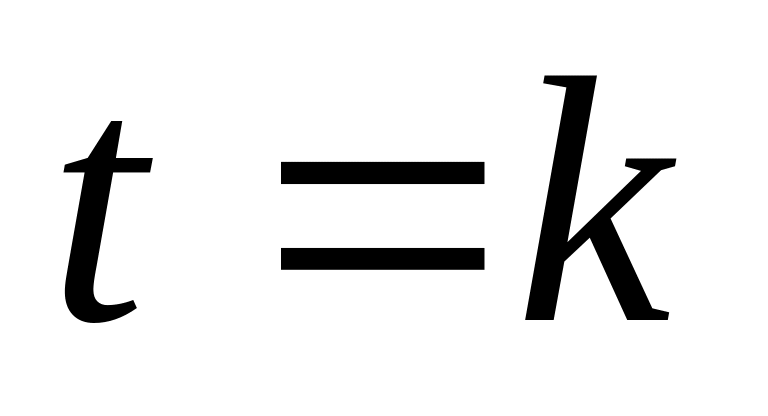 ,
використовуючи явну формулу:
,
використовуючи явну формулу:
![]() ,
,
![]() ,
,
![]() .**
.**
Обчислюємо величину
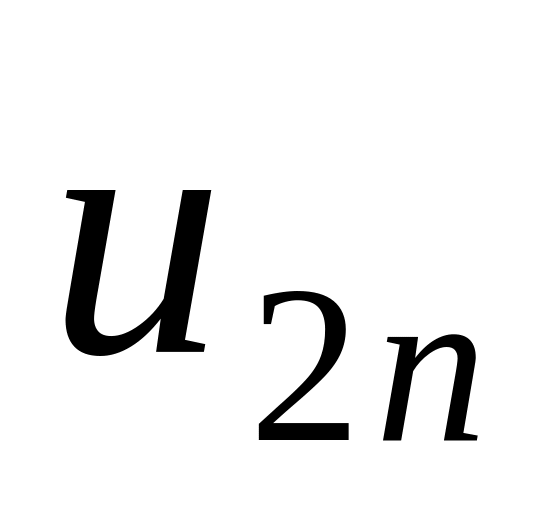 за формулою (5.6)
за формулою (5.6)
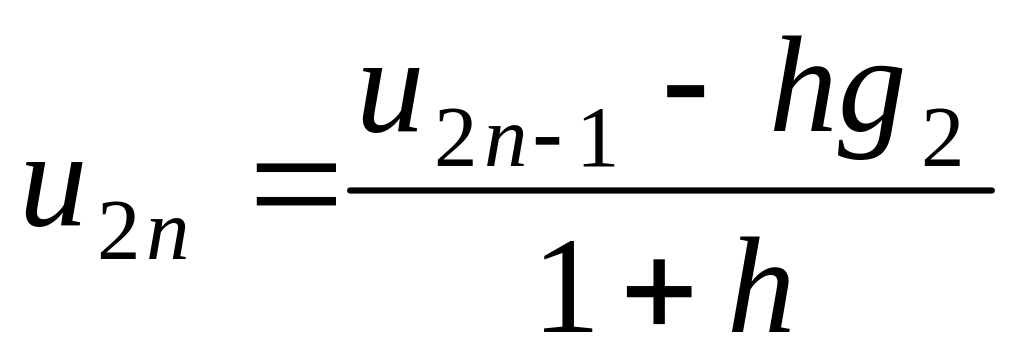 .
.
Завершивши
кроки 1-3 одержуємо розв'язок при
.
Для одержання розв'язку при
![]() повторюють кроки 2,3, піднімаючись щораз
на один рядок нагору, тобто збільшивши
повторюють кроки 2,3, піднімаючись щораз
на один рядок нагору, тобто збільшивши
![]() на одиницю й використовуючи
з попереднього рядка.
на одиницю й використовуючи
з попереднього рядка.
Явна схема відповідає верхньому шаблону, наведеному на рисунку 3.1.
Недолік
явної схеми:
якщо крок за часом
![]() виявляється досить великим у порівнянні
із кроком по
,
то погрішності обчислень можуть стати
настільки великими, що отриманий
розв'язок втрачає сенс, тобто розв'язок
стає нестійким. Для стійкості явної
схеми повинна
виконуватися умова
виявляється досить великим у порівнянні
із кроком по
,
то погрішності обчислень можуть стати
настільки великими, що отриманий
розв'язок втрачає сенс, тобто розв'язок
стає нестійким. Для стійкості явної
схеми повинна
виконуватися умова
![]() ,
,
яка
накладає досить жорсткі
обмеження на крок за часом (![]() ) і веде до значного збільшення часу
рахунку. Така схема називається умовно
стійкою.
) і веде до значного збільшення часу
рахунку. Така схема називається умовно
стійкою.
Приклад 3.1. Обчислити за допомогою явної схеми наближ
ений розв'язок змішаної задачі
![]() ,
,![]() ,
,
![]() ,
,
с
початковою умовою
![]() й граничними умовами
й граничними умовами
![]() .
.
Розв'язок.
Формула (5.5) з урахуванням кроків по
![]() -
-
![]() і по
-
і по
-
![]() після перетворень прийме вигляд:
після перетворень прийме вигляд:
![]() .
.
Схема
стійка, якщо
![]() .
Перевіримо:
.
Перевіримо:![]() ,
тобто обрана різницева схема є стійкою.
,
тобто обрана різницева схема є стійкою.

Рисунок 3.2 – Просторово - часова сітка для прикладу 3.1
З початкових умов одержимо:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ;
;
із граничних умов одержимо
![]() ,
,
![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Підрахуємо
значення для
![]() :
:
![]() ;
;
![]()
![]()
![]()
Аналогічно обчислюємо для інших значень .
Графіки розв'язку для чотирьох моментів часу наведені на рис. 5.3. Початковий розподіл температури позначений на графіку точками.
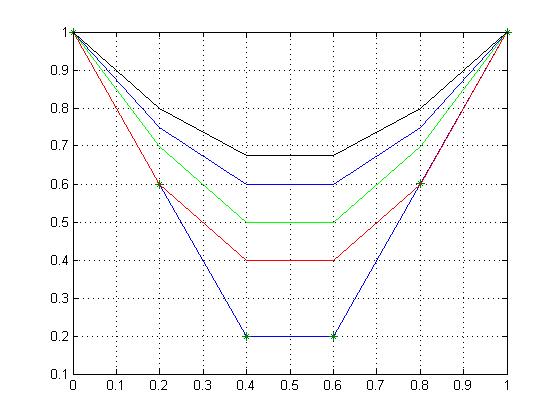 **
**
Рисунок 3.3 – Графіки розв'язку прикладу 3.1.
