3.7 Контрольні питання

1. Якого виду граничні умови використовуються в задачах параболічного типу?

2. Які види шаблонів використовуються в методі сіток у задачах параболічного типу? Яким чином будують на цих сітках різницеві апроксимації?

3. Опишіть метод прогону і його роль у розв'язку задач із ДРЧП.

4. З яких міркувань вибирають крок сітки в методі сіток?

5. У яких випадках може виникати нестійкість розв'язку задачі? Як впливає вибір параметрів сітки на стійкість?

6. Що розуміють під збіжністю процесу розв'язку задачі?

7. Що таке різницеві схеми підвищеної точності і які шаблони при цьому використовуються?

8. Як можна одержати апостеріорні оцінки погрішності отриманого розв'язку та уточнити розв'язок?

4 Метод сіток розв'язку крайових задач для хвильових рівнянь

4.1 Постановка задачі

Р озглянемо задачу поздовжніх коливань тонкого однорідного стрижня довжиною , коли його деформація залежить тільки від поздовжньої ( уздовж осі стрижня) координати й часу (рис. 6.1).

Рисунок 4.1 - Модель стрижня

Коливання стрижня описуються диференціальним рівнянням:

, (4.1)

де , і – модуль пружності й щільності матеріалу стрижня

с початковими умовами:

,

і граничними умовами:

, .

Для розв'язку задачі методом кінцевих різниць побудуємо прямокутну сітку (мал. 6.2), вузли якої визначаються формулами: , , , .

Значення на лівій, правій і нижній сторонах сітки відомі з початкових і граничних умов.

Р исунок 4.2 - Просторово-часова сітка й шаблон, що використовуються для рішення рівнянь гіперболічного типу

2. Явна схема

Замінимо частинні похідні в рівнянні (4.1) їх кінцево-різницевими апроксимаціями й підставимо їх у рівняння коливання. Одержимо:

Тут використовується п’яти точковий шаблон, представлений на рис. 4.2.

Отримане рівняння дозволяє виразити значення функції в момент часу через значення функції в попередні моменти часу:

.

Позначимо , приведемо подібні в останьому рівнянні і отримаємо розрахункову формулу для явної схеми:

(4.2)

У якості граничних умов по можуть використовуватися будь-які умови, що описують спосіб закріплення стрижня. Наприклад, тверде закріплення припускає нульове зрушення на кінцях стрижня. Це відповідає умові , . За часом у якості початкових умов задамо при вхідну деформацію стрижня й початкову швидкість його коливань , .

Алгоритм обчислень за явною схемою реалізується наступною послідовністю дій.

1. Визначимо деформацію стрижня в моменти й 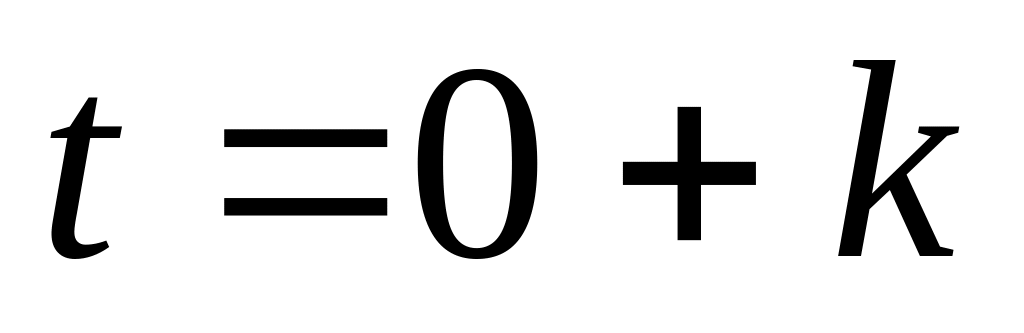. Для деформація відома з початкових умов . Для наступного моменту часу деформацію визначимо за допомогою другої початкової умови, що задає швидкість при :

, тоді , отже

(4.3)

Погрішність формули (4.3) .

2. Для одержання розв'язку при використовуємо формулу (4.2).

Схема (4.2)-(4.3) дає порядок апроксимації . Але порядок апроксимаціїї можна збільшити. Для цього введемо фіктивний часовий шар з вузлами , що лежатиме за межами області сітки. Значення сіткової функції на цьому шарі позначимо , . Для апроксимації похідної за часом у вузлах першого часового шару використаємо центральну симетричну різницю:

Відповідне різницеве рівняння запишется таким чином:

.

Звідки . Щоб виключити значення функції у фіктивному вузлі , використаємо різницеве рівняння (4.2), записавши його на нульовому шарі для :

Виключаємо з останього рівняння і використовуємо початкову умову, тоді отримуємо явну формулу для обчислення наближеного розв'язку на другому часовому шарі:

(4.4)

Різницева схема (6.2), (6.4) апроксимує диференціальну задачу з порядком .

Явна схема умовно стійка. Це означає, що при розв'язку гіперболічного рівняння за явною схемою слід обирати на крок по залежно від кроку по . Теоретично можна показати, що наближений розв'язок, що одержаний за допомогою (4.2), сходиться до точного при й зі швидкістю , якщо . При метод стає нестійким. Останнє означає, що при продовженні обчислень помилки катастрофічно наростають.

Приклад 4.1. Поздовжні коливання тяги описуються рівнянням ,***

де – модуль пружності, – щільність матеріалу стрижня. Тяга має довжину й закріплена на кінцях. Захопивши тягу в центрі, її деформують так, що поздовжнє переміщення стає рівним :

.

Потім тяга звільняється. Розрахуйте коливання при заданих параметрах. ***

, см	10	, Н/м^2	103
, см	1	, кг/м^2	103

Р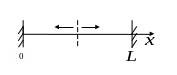 исунок 4.3 – Модель стрижня прикладу 4.1

Розв'язок. Побудуємо сітку, як показано на рис. 4.4.

Різницеве рівняння коливання струни

(з урахуванням кроків по й по відповідно: , ) після перетворень прийме вигляд:

.

Схема стійка, якщо . Перевіримо цю нерівність при заданих умовах задачі: , тобто схема є стійкою.

Із граничних умов одержимо:

, , , , , .

Тому що тяга закріплена на кінцях, маємо

, ; , ; , .

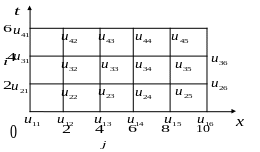
Рисунок 4.4 – Просторово-тимчасова сітка прикладу 4.1.

Так як , тоді , отже . Тобто для : , , , .

Підрахуємо значення для :

;

;

;

.

Аналогічно обчислюємо для інших значень .

Графік розв'язку, отриманий із кроком і із кроком за часом , наведений на рис. 4.5. Початкове положення стрижня показане на графіку точками, інші графіки відповідають моментам часу 1, 2, 3 і 4.

Погрішність розв'язку, як видно з порівняння графіків з наведеними розрахунками для , трохи менше 0.2, що становить майже половину абсолютного значення розв'язку. Це говорить про необхідність зменшення кроку по координаті й за часом відповідно. Розрахунки із кроком наведені на рис. 4.6 і показують, що погрішність розв'язку, оцінена за правилом Рунге, не перевищує абсолютного значення 0.05. (5% відносна погрішність).

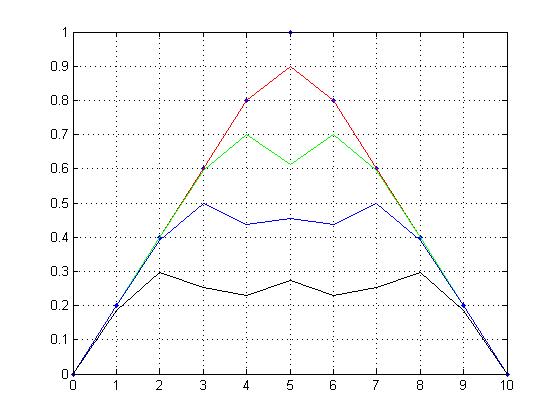
Рисунок 4.5 – Розв'язок задачі 4.1 із кроком

Рисунок 4.6 – Розв'язок задачі 4.1 із кроком