
- •1 Первообразная функция
- •2 Интегрирование по частям
- •3 Понятие о «не берущихся» интегралах.
- •5 Деление в ,,уголок’’
- •10 Интегрирование
- •8 Дать общий вид разложения правильного дробнорационального выр-я на сумму….
- •9 Интегрирование рациональных функций от sinx, cosx.
- •Частные случаи
- •11 Приближенное определение площади криволинейой трапеции.Риман
- •Пусть на отрезке [а,b] дана функция f(х), которую будем считать непрерывной.Построим разбиение отрезка [а,b]. Под разбиением будем понимать множество точек х0, х1, …, хn, удовлетворяющих условию:
- •12 Свойства определенного интеграла
- •13 Теорема о среднем для интеграла от непрерывной функции
- •14 Дифференцирование интеграла по верхнему пределу.
- •15 Формула Ньютона-Лейбница
- •17 Формула интегрирования по частям Можно пользоваться формулой ибо
- •26 Несобственный интеграл по полу- и –бесконечному промежуткам.
- •27 Простейшие свойства сходящихся несобственных интегралов с бесконечными пределами.
- •28 Несобственные интегралы от неограниченных функций(т.Е. Второго рода)
- •29 Определение главного зн. Для несоб. Инт. Второго рода
- •30 Признаки сходимости несобственного интеграпа
- •31 Понятие о условной сходимости
10 Интегрирование
![]() ;
;
![]() ;
dx//
рационально через dt
Несколько более общий случай:
;
dx//
рационально через dt
Несколько более общий случай:
![]() ,
где М – общий знаменатель
,
где М – общий знаменатель
![]()
8 Дать общий вид разложения правильного дробнорационального выр-я на сумму….
Пусть многочлен,
стоящий в знаменателе, удалось разложить
на множители:
![]() .
Тогда интеграл
.
Тогда интеграл![]() можно
существенно упростить за счет следующих
общих выкладок. Берем интеграл от каждого
слагаемого. Так, имеем:
можно
существенно упростить за счет следующих
общих выкладок. Берем интеграл от каждого
слагаемого. Так, имеем:
![]() =
=![]() Рациональные части от всех слагаемых
объединяем. Получаем в итоге равенство
Рациональные части от всех слагаемых
объединяем. Получаем в итоге равенство
![]() Здесь
многочлены Q1(x)
и Q2(x)
таковы:
Здесь
многочлены Q1(x)
и Q2(x)
таковы:
![]()
![]()
Оставшийся интеграл
достаточно простой. При нахождении
коэффициентов многочленов исходим из
последовательности равенств: 1)
![]() 2)
2)
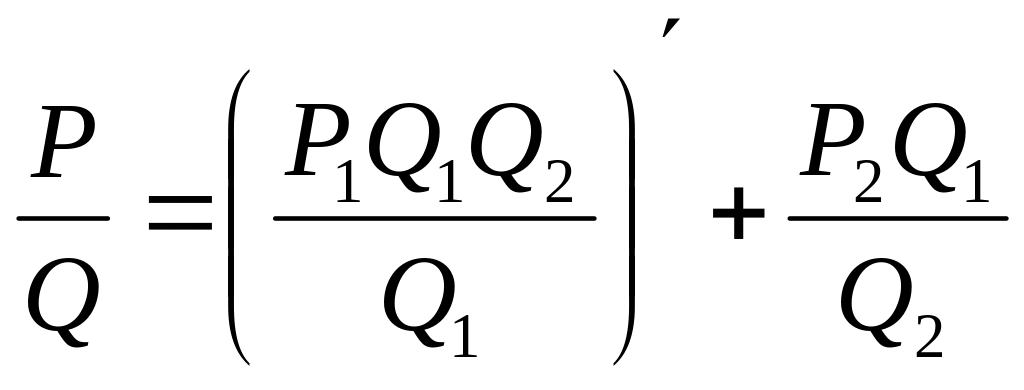 3)
3)
![]()
9 Интегрирование рациональных функций от sinx, cosx.
Рассмотрим
неопределенный интеграл![]() где R(
, ) – рациональная функция от sin
x
и cos
x.
Этот интеграл может быть в общем случае
сведен к интегралу от рациональной
функции, для чего надо подставить
где R(
, ) – рациональная функция от sin
x
и cos
x.
Этот интеграл может быть в общем случае
сведен к интегралу от рациональной
функции, для чего надо подставить
![]() .
.
Имеем
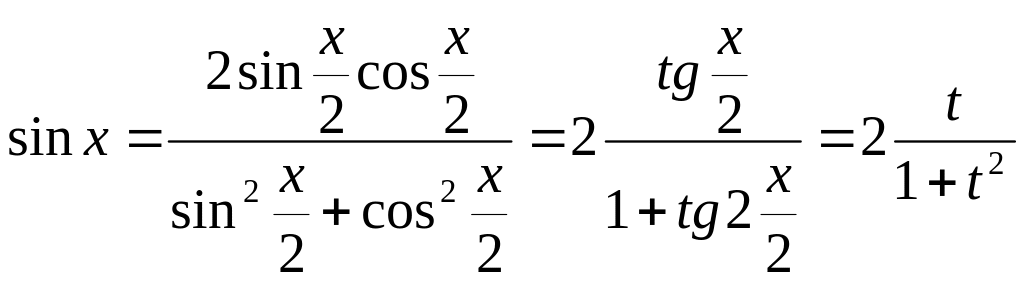
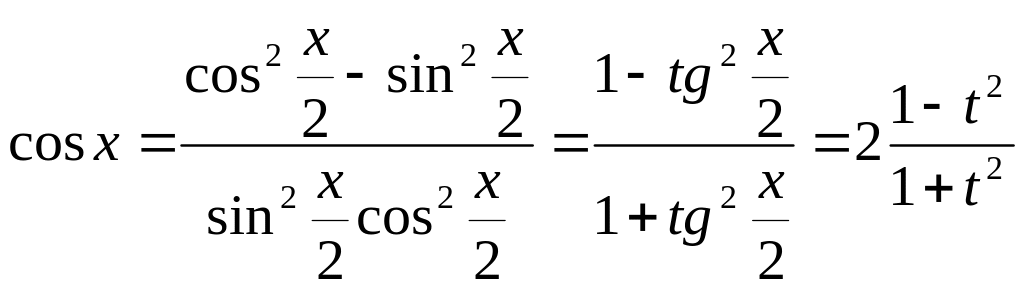
х=2arctgt![]()
![]()
Частные случаи
![]()
если
 или
или
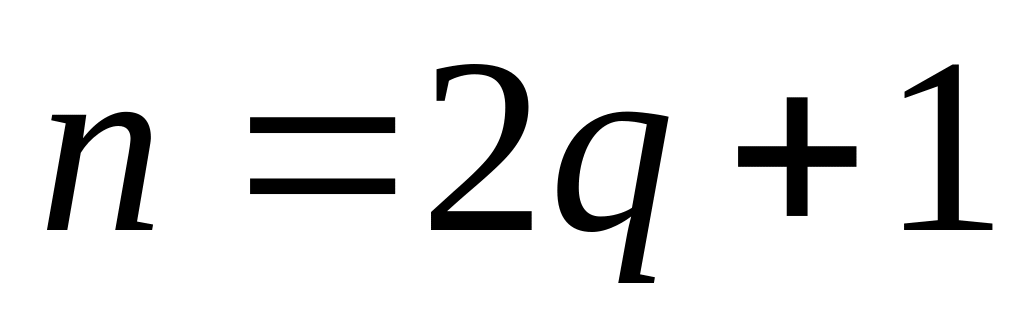 ,
то можно не применять универсальную
подстановку. Пусть, например, m-
нечетное
,
то можно не применять универсальную
подстановку. Пусть, например, m-
нечетное
а)
![]()
б)
![]()
2.
![]() и
и
![]() .
Тогда понижаем порядок вдвое, приходим
к интегралу вида
.
Тогда понижаем порядок вдвое, приходим
к интегралу вида
![]() .После
возведения в степени p
и q
и перемножения, снова имеем интегралы
вида
.После
возведения в степени p
и q
и перемножения, снова имеем интегралы
вида
![]() Пример
Пример
![]() =
=![]()
11 Приближенное определение площади криволинейой трапеции.Риман
Требуется определить площадь криволинейной трапеции АВСД, ограниченной сверху кривой y = f(х), слева и справа прямыми х=а и х=b и снизу прямой у = 0 (осью х). Сначала рассмотрим приближенное решение этой задачи. Разобьем [а,b] точками х0=а, х1, х2,…,хn-1, хn=b; хj-хj-1=Δ хj-1.
Проведем ординаты (вычислим) f(х0), f(х1), …, f(хn-1), f(хn).
Вычислим суммарную площадь прямоугольников высоты f(х0)…, f(хn-1)
Имеем
![]()
Величину σ можно рассматривать в качестве приближенного значения площади. Сумма Σ f(хj) Δхj является примером интегральной суммы.
Разбиение отрезка [а,b] можно характеризовать в данном случае максимальным значением Δхj, которое обозначим λ:
λ=max(Δxj) j=0,1,...,n-1 λ- параметр разбиения. Ему соответствует сумма площадей σ.
Возьмем более
«мелкое» разбиение с параметром λ', λ'<λ
. Ему соответствует сумма площадей
прямоугольников:![]() Измельчая разбиения и устремления
параметра λ к нулю, получим последовательность
интегральных сумм σ, σ', σ",… Если эта
последовательность имеет предел при
λ→0, равный S, что можно записать так
Измельчая разбиения и устремления
параметра λ к нулю, получим последовательность
интегральных сумм σ, σ', σ",… Если эта
последовательность имеет предел при
λ→0, равный S, что можно записать так
![]() то этот предел принимают (по определению)
за площадь криволинейной трапеции АВСД.
то этот предел принимают (по определению)
за площадь криволинейной трапеции АВСД.
Интеграл Римана (определенный интеграл)
Пусть на отрезке [а,b] дана функция f(х), которую будем считать непрерывной.Построим разбиение отрезка [а,b]. Под разбиением будем понимать множество точек х0, х1, …, хn, удовлетворяющих условию:
а= х0< х1<х2<…< хn-1< хn=b
Сумма
![]() называется интегральной
суммой для произвольной
функции f(х) на отрезке [а,b]
. Если существует предел (конечный)
называется интегральной
суммой для произвольной
функции f(х) на отрезке [а,b]
. Если существует предел (конечный)
![]() ,не
зависящий от выбора точек ξj
на интервалах [хj,
хj+1]
и от выбора точек хj,
то такой предел называют определенным
интегралом
от f(х); обозначается символом
,не
зависящий от выбора точек ξj
на интервалах [хj,
хj+1]
и от выбора точек хj,
то такой предел называют определенным
интегралом
от f(х); обозначается символом
![]() Итак
Итак
![]() a
называется нижним пределом интегрирования,
b
– верхним
пределом интегрирования, f(х) называют
подынтегральной функцией, f(х)dх –
подынтегральное выражение.
a
называется нижним пределом интегрирования,
b
– верхним
пределом интегрирования, f(х) называют
подынтегральной функцией, f(х)dх –
подынтегральное выражение.
Функции f(х), для
которых существует конечный предел
![]() ,
называют
,
называют
интегрируемыми в смысле Римана (мы будем иметь дело только с таким интегралом) .
