2. Морфизмы топологических пространств.

Def. f:XY называется непрерывным, если прообраз f^-1(B) открыт в ТП Х В, открытого в Y.

Упражнение 29.

А) f:XY непрерывно  прообразы замкнутых множеств замкнуты.

В) композиция непрерывных отображений непрерывна.

С) тождественное отображение непрерывно.

D) Сужение f|_A:AY непрерывного f:XY на АХ непрерывно.

Е) включение подмножества АХ в ТП Х непрерывно.

Упражнение 30.

Для непрерывности f:X®Y достаточно открытости прообразов некоторой предбазы ТП Y.

Def. Непрерывное отображение называется открытым, если образы открытых множеств открыты и замкнутым, если образы замкнутых множеств замкнуты.

Отображение f:XY называется непрерывным в точке хХ, если  окрестности V(f(x))  окрестность U(x) такая, что f(U)V.

Упражнение 31.

1. открытость и замкнутость отображений сохраняется при композиции.

2. Пусть B=В(f(x)) – база окрестностей точки f(x), а Г(х) – предбаза окрестностей точки х. Тогда f:X®Y непрерывно в х  любая VB содержит образ некоторой UГ.

3. f:X®Y непрерывно  оно непрерывно в каждой точке.

Упражнение 32*.

Приведите пример непрерывной биекции, обратное отображение к которой не непрерывно.

Def. Биекция f:X®Y такая, что и f и f^-1 непрерывны, называется гомеоморфизмом. Пространства, между которыми можно установить гомеоморфизм, называются гомеоморфными. С топологической точки зрения они эквивалентны. Топология изучает свойства множеств, инвариантные относительно гомеоморфизмов. Множество гомеоморфизмов f:X®Х образует, конечно, группу.

До сих пор у нас морфизмами назывались отображения, коммутировавшие с операциями (в случаях групп, колец, ВП) или с операцией сравнения в случае упорядоченных множеств.

Упражнение 33.

А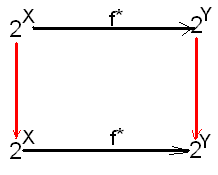 что можно сказать об операторе, коммутирующим с операторами замыкания, т.е. таким, для которого следующая диаграмма коммутативна (вертикальные красные стрелки означают замыкания в соответствующих топологических пространствах): f* - индуцированное отображением f:ХY отображение подмножеств ТП Х в подмножества ТП Y. Множества всех подмножеств Х и Y обозначены, как обычно, 2^Х и 2^Y соответственно.

Упражнение 34.

Сформулируйте определение непрерывного отображения в случае, когда оба пространства – метрические. Потом повторите его для f:RⁿR^m и затем, наконец, для случая f:RR. Для непрерывности в точке приведите его к форме «-» определения: «>0 |…»

Def. ТП называется связным, если его нельзя представить в виде объединения двух непересекающихся открытых подмножеств.

Упражнение 35.

Докажите, что это определение эквивалентно тому, что в пространстве нет подмножеств, открытых и замкнутых одновременно, кроме него самого и пустого множества.

Упражнение 36. Докажите, что при непрерывном отображении а) образом связного множества является связное множество,

b) образом компактного множества является компактное множество. Таким образом, свойства ТП быть связным или компактным являются топологическими, т.е., инвариантными относительно гомеоморфизмов.

Иерархия классов топологических пространств.

Самый общий класс ТП, так называемые Т₀-пространства, выделены А.Н.Колмогоровым. Это такие пространства, в которых для каждой пары точек, по крайней мере, у одной из них имеется окрестность, не содержащая другую точку.

Упражнение 37.

Докажите, что Т₁-пространства являются Т₀-пространствами. Приведите пример (возьмите пространство из трёх точек, например) Т₀-пространства, не являющегося Т₁-пространством. Таким образом, класс Т₀-пространств, действительно, шире класса Т₁-пространств.

Def. ТП называется Т₂-пространством, или хаусдорфовым пространством, если любые две различные точки обладают непересекающимися окрестностями.

Упражнение 38.

Докажите, что Т₂-пространства являются Т₁-пространствами (это почти очевидно). Приведите пример (это уже не столь просто) Т₁-пространства, которое не было бы Т₂-пространством. Таким образом, класс Т₁-пространств, действительно, шире класса Т₂-пространств.

Def. «Аксиома Т₃»: у каждой точки и у каждого не содержащего её замкнутого множества имеются непересекающиеся окрестности. «Аксиома Т₄»: у любых двух непересекающихся замкнутых множеств есть непересекающиеся окрестности.

Упражнение 39.

А) Аксиома Т₃ эквивалентна следующему утверждению: каждая окрестность каждой точки содержит замыкание некоторой другой окрестности этой точки.

В) Аксиома Т₄ эквивалентна следующему утверждению: каждая окрестность замкнутого множества содержит замыкание некоторой другой окрестности этого множества.

С) Т₄  любой конечный набор попарно непересекающихся замкнутых множеств можно вписать в окрестности с попарно непересекающимися замыканиями.

Упражнение 40*.

Приведите примеры ТП, удовлетворяющих аксиоме Т₃ и даже Т₄, но не являющихся при этом даже Т₁-пространствами!

Этим обстоятельством мотивированы следующие определения:

Def. ТП, для которых выполняются аксиомы Т₃ и Т₁ (для любой пары точек у каждой из них имеется окрестность, не содержащая другую; проверьте эквивалентность этого утверждения аксиоме №5 нашего определения ТП) называются регулярными, а ТП, в которых выполняются аксиомы Т₄ и Т₁ называются нормальными.

Упражнение 41.

Нормальностьрегулярностьхаусдорфовость.

Подпространства хаусдорфова ТП хаусдорфовы, регулярного ТП – регулярны, и замкнутые подпространства нормального ТП – нормальны.

Def. Топологии, заданные на одном и том же множестве частично упорядочены: топология А считается сильнее или тоньше топологии В, если все множества, открытые в В, открыты также и в А (если верно также и обратное, то они эквивалентны). Топология В при этом считается слабее или грубее топологии А. Сильнейшей из возможных является топология, в которой все вообще подмножества считаются открытыми (при этом, разумеется, все они же и замкнуты, так что оператор замыкания просто тождественен). Такая топология называется дискретной. Слабейшей из всех возможных является топология, в которой всего два подмножества открыты (они же и замкнуты) – все множество и его пустое подмножество.

Такая топология называется тривиальной.

Def. Точка р называется предельной точкой (= точкой накопления) множества М, если р . Множество dМ=М^d всех предельных точек множества М называется производным множеством (или производной) множества М. Если же рМ\М^d, то она называется изолированной точкой множества М.

Упражнение 42.

Точка р является предельной точкой множества М  любая окрестность точки р содержит точки множества М, отличные от самой точки р. Соответственно, для того чтобы точка р была изолированной, необходимо и достаточно, чтобы существовала окрестность точки р, не содержащая никаких точек М, кроме самой р.

Упражнение 43.

Докажите, что рМ^d  каждая окрестность точки р содержит бесконечно много точек из М.

Таким образом, рМ^d  множество М не является локально конечным в точке р.

Докажите следующие формулы:

Упражнение 44.

1. (XY)^d=X^dY^d;

2. X^d\Y^d(X\Y)^d;

3. d²X=d(dX))d(X);

4. ;

5. ;

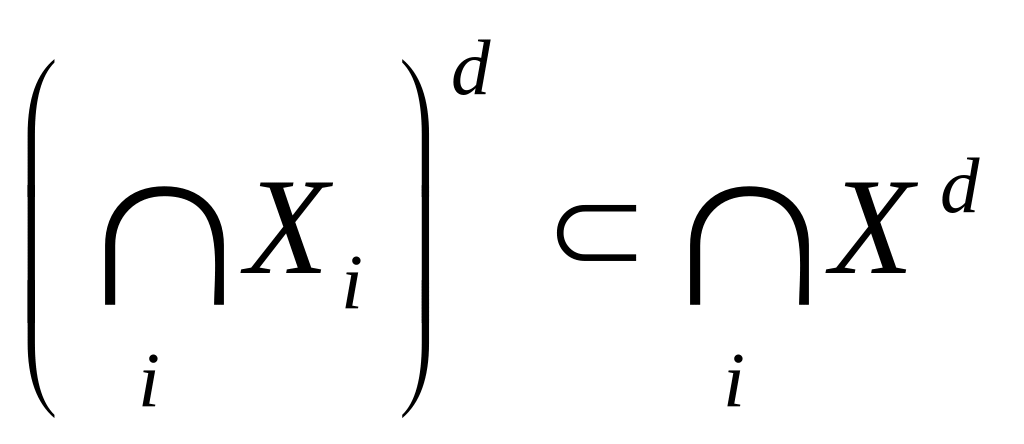6. (XY)X^dY^d;

7. d =dX;

8. =XdX.

Def. Множество, состоящее из одних только изолированных точек, называется дискретным.

Множество, не содержащее изолированных точек, называется плотным в себе. Замкнутое множество, плотное в себе называется совершенным.

Упражнение 45.

1. Любое конечное множество дискретно.

2. Любое подмножество дискретного множества дискретно.

3. Точка р является изолированной точкой ТП Т  точка р является открытым множеством в ТП Т. Т.о., ТП Т дискретно  все его подмножества открыты!

4. Подмножество ТП замкнуто  оно содержит все свои предельные точки.

Упражнение 46.

1. Множество Х совершенно  X=dX.

2. Х плотно в себе  совершенно.

3. Объединение любого числа плотных в себе множеств плотно в себе.

4. Если пространство плотно в себе, то каждое открытое и каждое всюду плотное множество плотны в себе.

Упражнение 47.

Пусть А – несчётное подмножество пространства со счётной базой. Тогда А обладает, по крайней мере, одной предельной точкой.

Упражнение 48.

Пространство со счётной базой является пространством Линделёфа (финально компактным).

Def. Про пространства со счётной базой говорят также, что они удовлетворяют второй аксиоме счётности. Говорят, что пространство удовлетворяет первой аксиоме счётности, если система окрестностей каждой его точки обладает счётной базой.

Упражнение 49.

Докажите, что из второй аксиомы счётности следует первая, и приведите пример пространства, удовлетворяющего первой аксиоме счётности и не удовлетворяющего второй.