
Определители.
Начнём издалека, с самого начала, беглым обзором охватив весь путь, приводящий к построению теории определителей – важнейшего инструмента в исследовании линейных преобразований (и не только них).
Решая систему двух уравнений с двумя неизвестными
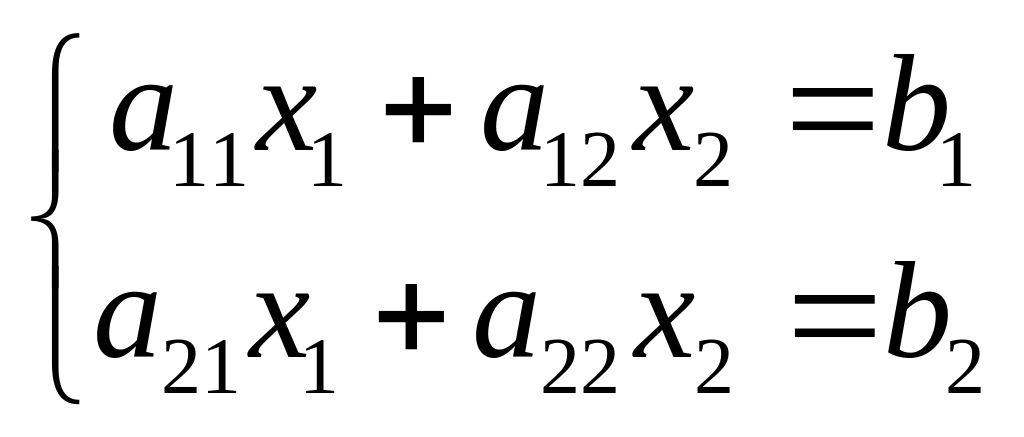 (1),
мы обнаружили, что имеет она
единственное решение (пару элементов
х1, х2 поля F
или, говоря иначе, вектор (x1,x2)F2)
в том и только в том случае, если величина
a11a22-a12a210.
Эту величину мы назвали определителем
матрицы А=
(1),
мы обнаружили, что имеет она
единственное решение (пару элементов
х1, х2 поля F
или, говоря иначе, вектор (x1,x2)F2)
в том и только в том случае, если величина
a11a22-a12a210.
Эту величину мы назвали определителем
матрицы А=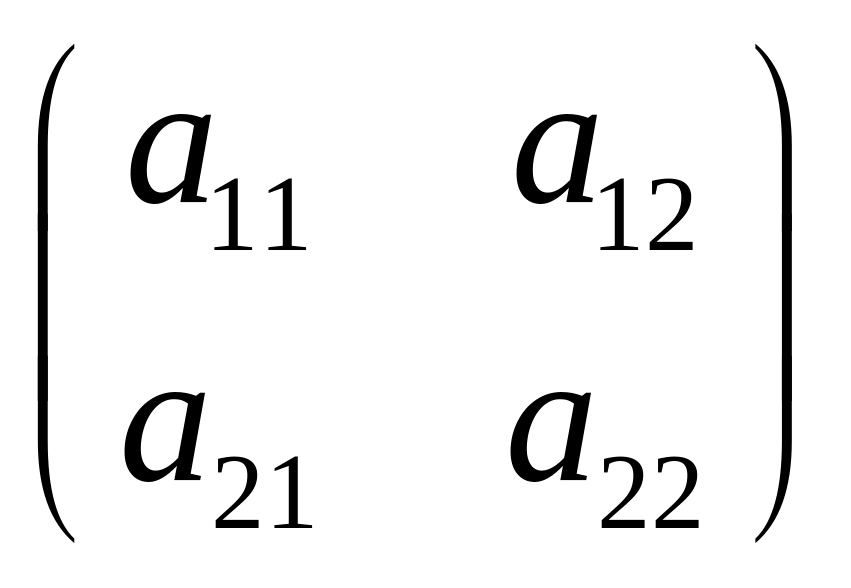 ,
а саму систему переписали в векторном
виде:
,
а саму систему переписали в векторном
виде:
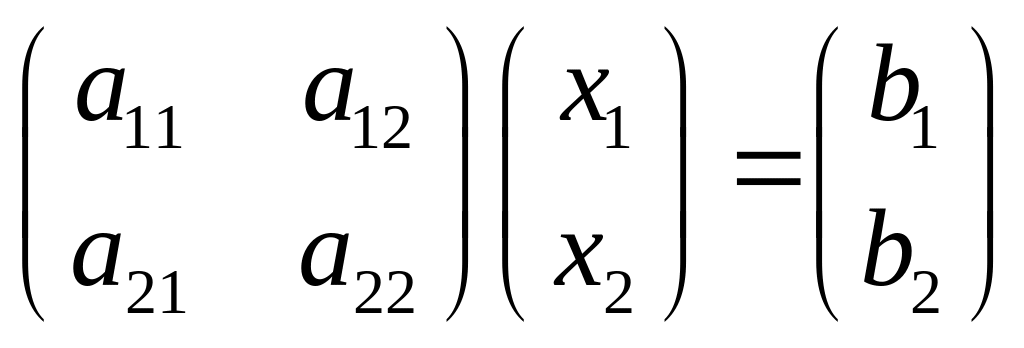 или АХ=В, где Х и В –
вектора (искомый и данный соответственно),
а А – линейный оператор, соответствующий
матрице А в стандартном базисе.
Если
мы исключим из системы (1) неизвестное
х2, умножив первое уравнение на
a22, второе на (-a12)
и сложив, то получим
или АХ=В, где Х и В –
вектора (искомый и данный соответственно),
а А – линейный оператор, соответствующий
матрице А в стандартном базисе.
Если
мы исключим из системы (1) неизвестное
х2, умножив первое уравнение на
a22, второе на (-a12)
и сложив, то получим
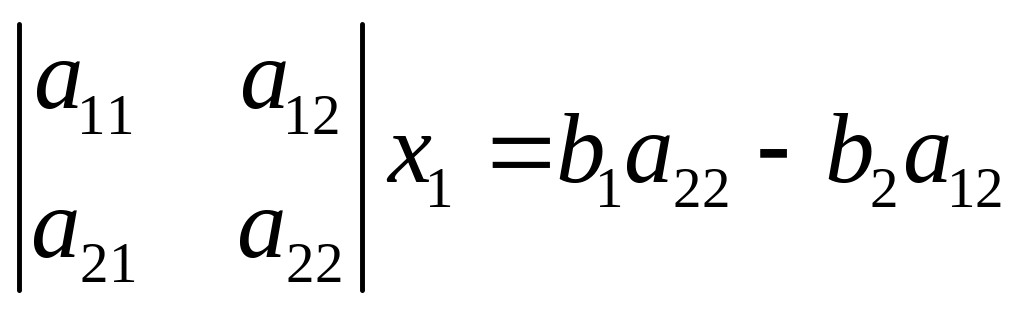 .
Правая часть – это тоже определитель,
определитель матрицы
.
Правая часть – это тоже определитель,
определитель матрицы
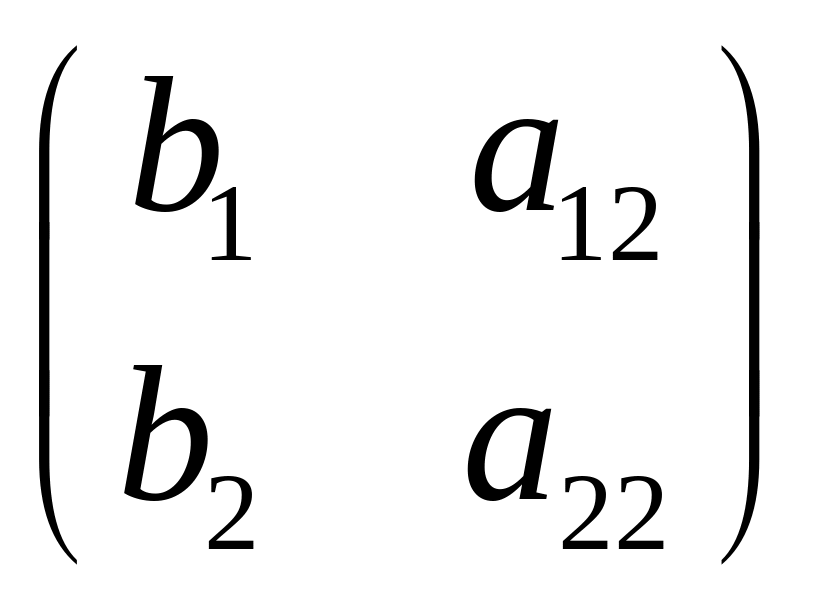 .
Получаем в итоге:
.
Получаем в итоге:
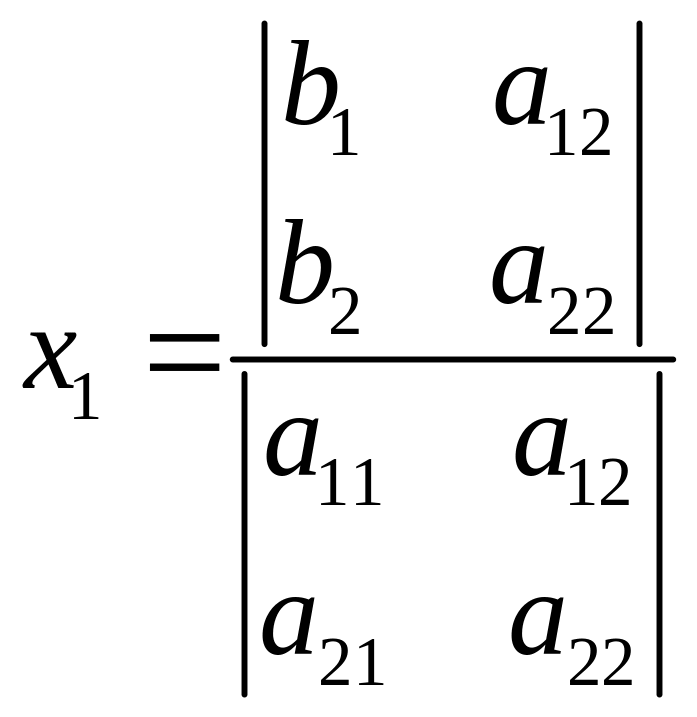 и, аналогично,
и, аналогично,
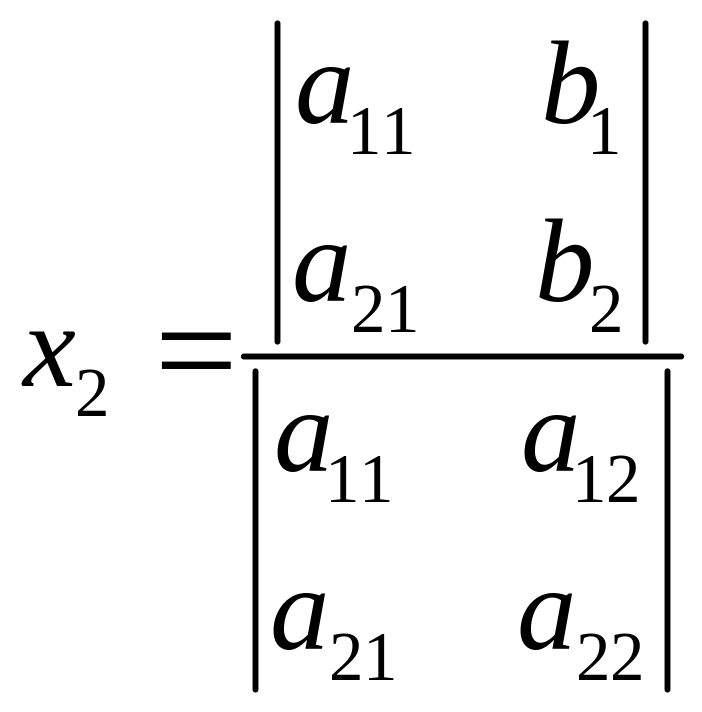 . (2)
Теперь
рассмотрим систему двух однородных
уравнений с тремя неизвестными:
. (2)
Теперь
рассмотрим систему двух однородных
уравнений с тремя неизвестными:
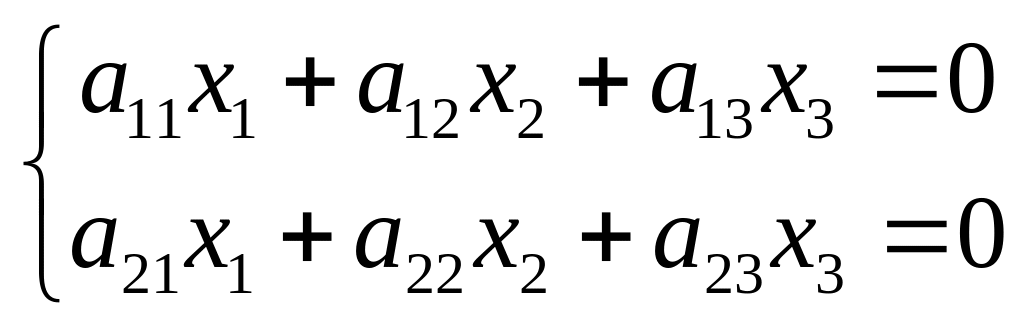 (3)
Если
мы найдём хотя бы одно ненулевое
решение этой системы – вектор
х=(х1,х2,х3), то
решением будет и любой коллинеарный
ему вектор х=(х1,х2,х3),
то есть вся прямая, содержащая вектор
х или порождённая вектором х
(его линейная оболочка, в данном случае
– одномерное подпространство F3).
Если ненулевое решение существует, то
хотя бы один из хi0
i=1,2,3. Допустим, что это
так и х30.
Тогда разделив уравнения на х3
и введя новые переменные y1=-x1/x3;
y2=-x2/x3
получим систему
(3)
Если
мы найдём хотя бы одно ненулевое
решение этой системы – вектор
х=(х1,х2,х3), то
решением будет и любой коллинеарный
ему вектор х=(х1,х2,х3),
то есть вся прямая, содержащая вектор
х или порождённая вектором х
(его линейная оболочка, в данном случае
– одномерное подпространство F3).
Если ненулевое решение существует, то
хотя бы один из хi0
i=1,2,3. Допустим, что это
так и х30.
Тогда разделив уравнения на х3
и введя новые переменные y1=-x1/x3;
y2=-x2/x3
получим систему ,
которую мы уже умеем решать. В качестве
порождающего одномерное пространство
всех решений системы (3) вектора можно
взять вектор с координатами x1=
,
которую мы уже умеем решать. В качестве
порождающего одномерное пространство
всех решений системы (3) вектора можно
взять вектор с координатами x1= ,
x2=-
,
x2=-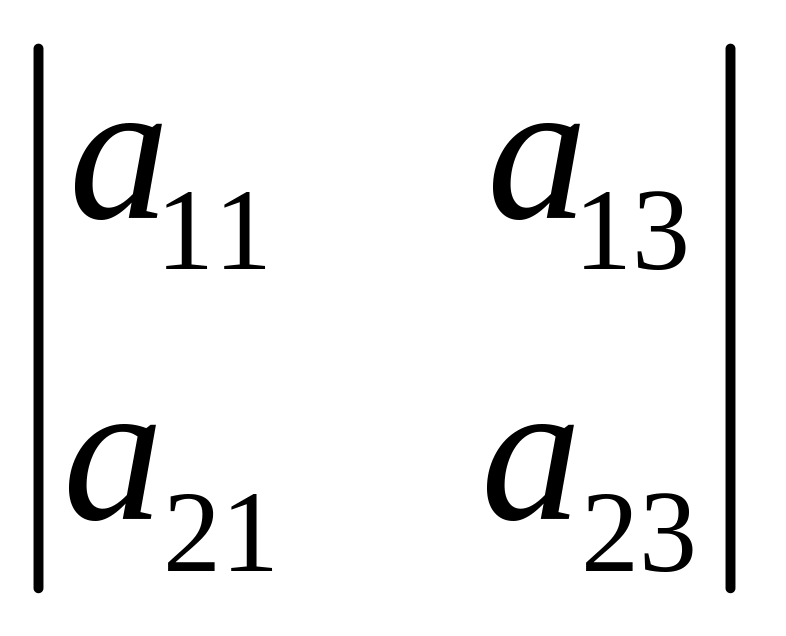 ,
x3=
,
x3=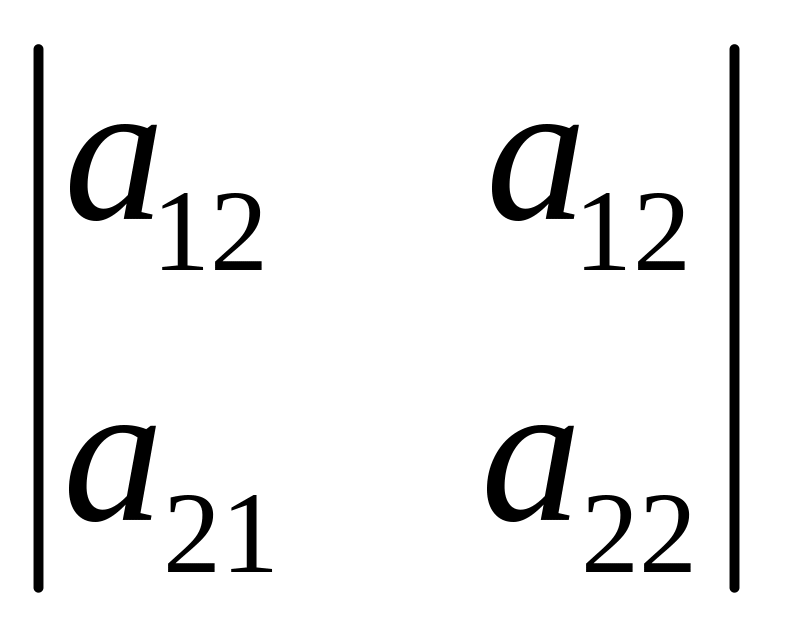 (4).
(4).
Упражнение 10. Формулы (4) были выведены в предположении, что 0. Докажите, что они имеют место, если хотя бы один (любой) из этих трёх определителей 0. Приведите пример, когда в случае равенства нулю всех трёх определителей у системы (3) имеются ненулевые решения.
П
 ереходим
к системам трёх уравнений с тремя
неизвестными:
ереходим
к системам трёх уравнений с тремя
неизвестными:
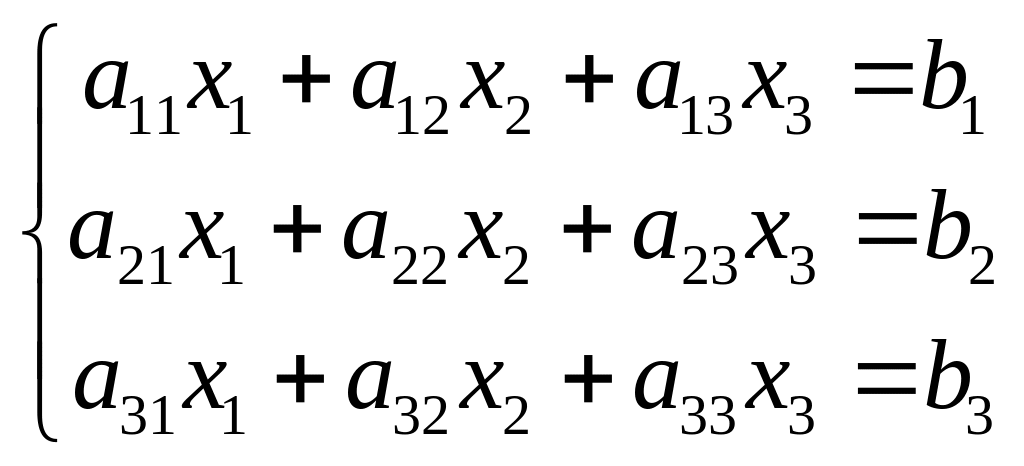 (5)
Решим
её также как и систему двух уравнений
с двумя неизвестными методом Гаусса
исключения неизвестных. Подберём
множители с1, с2 и с3
так, чтобы умножив на них соответственно
первое, второе и третье уравнения и
затем сложив, мы бы избавились от
неизвестных х2 и х3. Это
приводит нас к системе двух однородных
уравнений с тремя неизвестными - с1,
с2 и с3, аналогичную системе
(3):
(5)
Решим
её также как и систему двух уравнений
с двумя неизвестными методом Гаусса
исключения неизвестных. Подберём
множители с1, с2 и с3
так, чтобы умножив на них соответственно
первое, второе и третье уравнения и
затем сложив, мы бы избавились от
неизвестных х2 и х3. Это
приводит нас к системе двух однородных
уравнений с тремя неизвестными - с1,
с2 и с3, аналогичную системе
(3):
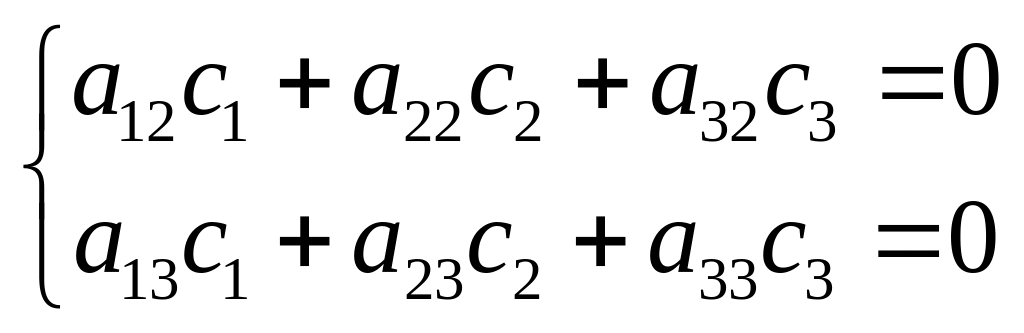 .
После
решения в соответствии с (4) и подстановки
в первое уравнение, получим:
.
После
решения в соответствии с (4) и подстановки
в первое уравнение, получим:
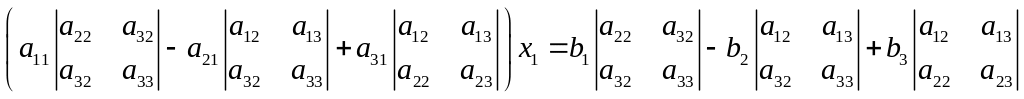 (6).
Таким
образом, | | третьего
порядка определяется при помощи
определителей второго порядка:
(6).
Таким
образом, | | третьего
порядка определяется при помощи
определителей второго порядка:
 (7).
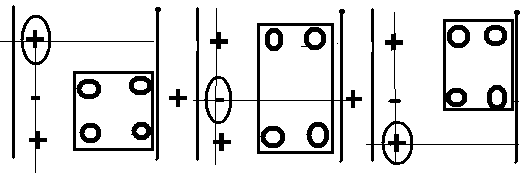
Графически
выражение в правой части (7) получается
разложением определителя в левой части
по первому столбцу:
Именно: берётся
элемент из первого столбца с
соответствующим знаком (весь определитель
размечен в шахматном порядке знаками
«+» и «-»
начиная с левого верхнего угла, в
который помещён знак «+») и умножается
на определитель на единицу меньшего
порядка (в данном случае – второго)
который получается, если вычеркнуть
тот столбец и ту строку, в которой стоит
этот элемент.
Def.
Определитель матрицы, получающийся
вычёркиванием из матрицы А=(ai,j)
i-ой строки и j-го
столбца называется минором
Мi,j
матрицы А, соответствующим элементу
ai,j.
Аi,j=(-1)i+jMi,j
называется алгебраическим
дополнением элемента ai,j.
Появляется
возможность, продолжая действовать в
том же духе, получать уравнения и
определители всё больших порядков,
опираясь на уже известные формулы и
определители меньших порядков.
Def.
Итак, первое
(индуктивное)
определение определителя n-го
порядка:
detA=
a1,1M1,1-a2,1M2,1+a3,1M3,1-…+(-1)n+1an,1Mn,1=a1,1A1,1+a2,1A2,1+a3,1A3,1+…+an,1An,1.
В
этом разложении (по первому столбцу)
все миноры, а, соответственно, и все
алгебраические дополнения уже определены
к этому моменту, так как они – определители
(n-1)-го порядка.
Упражнение
11*.
Докажите, что тот же
результат получится, если разлагать
исходный определитель не по первому,
а по любому столбцу, а также и по любой
строке.
Упражнение
12*.
Докажите, что
определённая таким образом функция
на квадратных матрицах является
линейной функцией как строк, так и
столбцов матриц А=(ai,j)
n-го порядка.
Упражнение
13.
Докажите,
что функция detA на
матрицах n-го порядка
является кососимметрической функцией
как строк, так и столбцов этих матриц
(то есть, меняет знак при перестановке
любых двух строк или столбцов).
Возвращаясь к уравнению (6), обратите
внимание, что правая часть этого
уравнения является также разложением
по первому столбцу определителя, в
котором первый столбец в определителе
третьего порядка из (7) заменён столбцом
из правых частей системы (5). Таким
образом, получаем формулы для корней
системы (5):
(7).
Графически
выражение в правой части (7) получается
разложением определителя в левой части
по первому столбцу:
Именно: берётся
элемент из первого столбца с
соответствующим знаком (весь определитель
размечен в шахматном порядке знаками
«+» и «-»
начиная с левого верхнего угла, в
который помещён знак «+») и умножается
на определитель на единицу меньшего
порядка (в данном случае – второго)
который получается, если вычеркнуть
тот столбец и ту строку, в которой стоит
этот элемент.
Def.
Определитель матрицы, получающийся
вычёркиванием из матрицы А=(ai,j)
i-ой строки и j-го
столбца называется минором
Мi,j
матрицы А, соответствующим элементу
ai,j.
Аi,j=(-1)i+jMi,j
называется алгебраическим
дополнением элемента ai,j.
Появляется
возможность, продолжая действовать в
том же духе, получать уравнения и
определители всё больших порядков,
опираясь на уже известные формулы и
определители меньших порядков.
Def.
Итак, первое
(индуктивное)
определение определителя n-го
порядка:
detA=
a1,1M1,1-a2,1M2,1+a3,1M3,1-…+(-1)n+1an,1Mn,1=a1,1A1,1+a2,1A2,1+a3,1A3,1+…+an,1An,1.
В
этом разложении (по первому столбцу)
все миноры, а, соответственно, и все
алгебраические дополнения уже определены
к этому моменту, так как они – определители
(n-1)-го порядка.
Упражнение
11*.
Докажите, что тот же
результат получится, если разлагать
исходный определитель не по первому,
а по любому столбцу, а также и по любой
строке.
Упражнение
12*.
Докажите, что
определённая таким образом функция
на квадратных матрицах является
линейной функцией как строк, так и
столбцов матриц А=(ai,j)
n-го порядка.
Упражнение
13.
Докажите,
что функция detA на
матрицах n-го порядка
является кососимметрической функцией
как строк, так и столбцов этих матриц
(то есть, меняет знак при перестановке
любых двух строк или столбцов).
Возвращаясь к уравнению (6), обратите
внимание, что правая часть этого
уравнения является также разложением
по первому столбцу определителя, в
котором первый столбец в определителе
третьего порядка из (7) заменён столбцом
из правых частей системы (5). Таким
образом, получаем формулы для корней
системы (5):
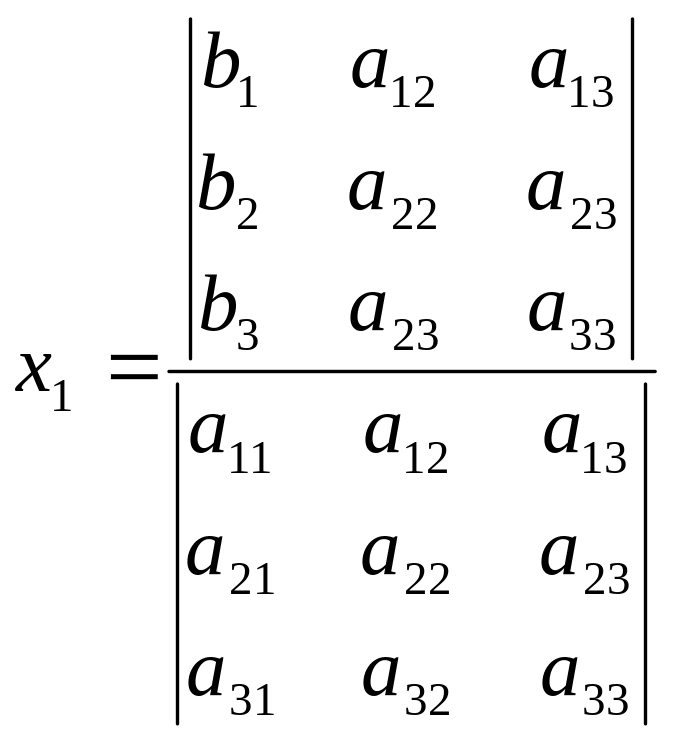 и,
аналогично,
и,
аналогично,
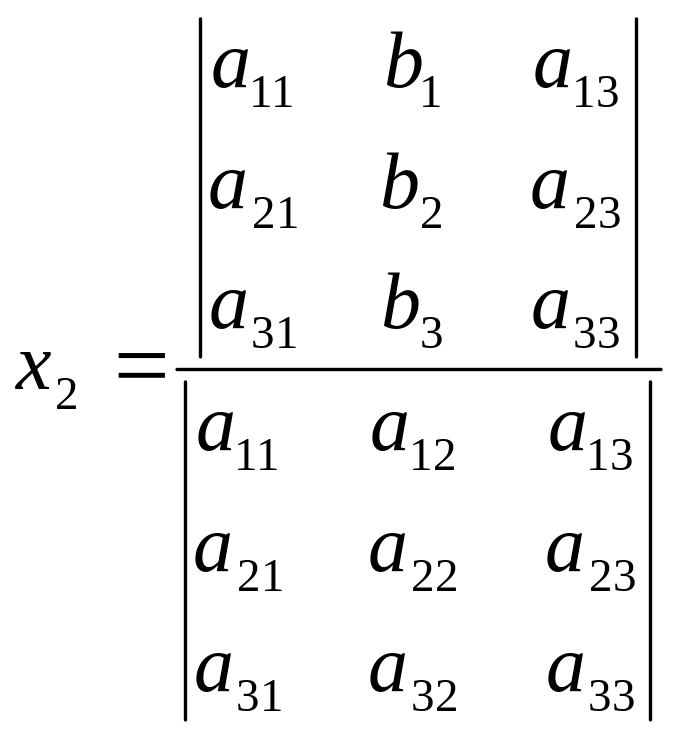 и
и
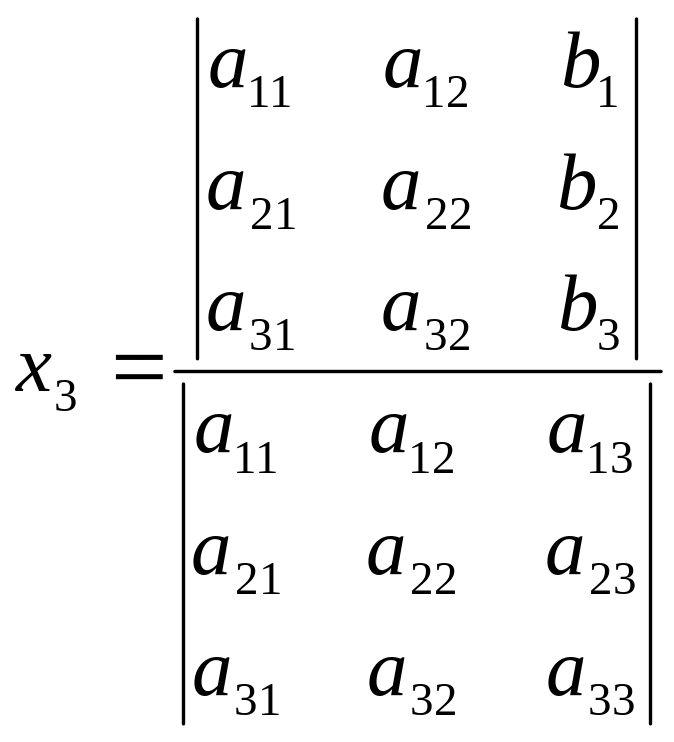 (8).
Формулы
(2) и (8) называются формулами
Крамера для определителей второго
и третьего порядка соответственно. Мы
ожидаем, естественно, что эти правила
сохранятся и для определителей высших
порядков.
Этим, по крайней мере,
теоретически, будет закрыт вопрос о
корнях линейной системы из n
уравнений с n неизвестными
ранга n.
Проведём
надлежащую подготовку к доказательству
этой гипотезы.
(8).
Формулы
(2) и (8) называются формулами
Крамера для определителей второго
и третьего порядка соответственно. Мы
ожидаем, естественно, что эти правила
сохранятся и для определителей высших
порядков.
Этим, по крайней мере,
теоретически, будет закрыт вопрос о
корнях линейной системы из n
уравнений с n неизвестными
ранга n.
Проведём
надлежащую подготовку к доказательству
этой гипотезы.Забудем на время о том определении определителя (индуктивном), которое у нас уже было, и вспомним, наоборот, о том результате, к которому мы пришли в конце конспекта «Vector spaces-I»; упражнения 70-74. Итак, мы искали функцию
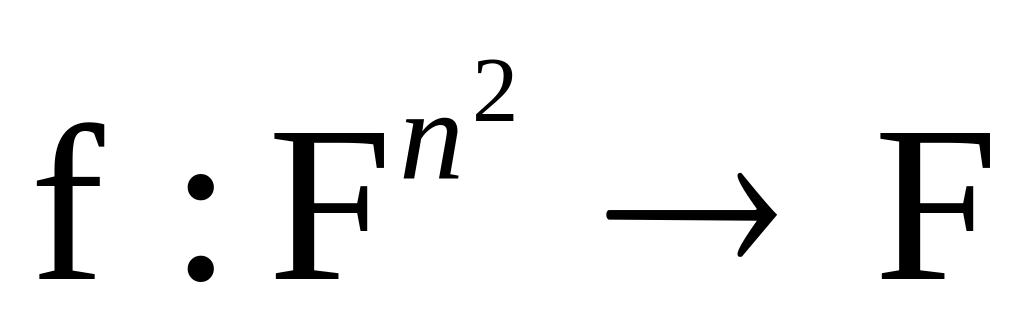 ,
полилинейную на векторах-строках
A1,
A2, …,An
матриц
,
полилинейную на векторах-строках
A1,
A2, …,An
матриц
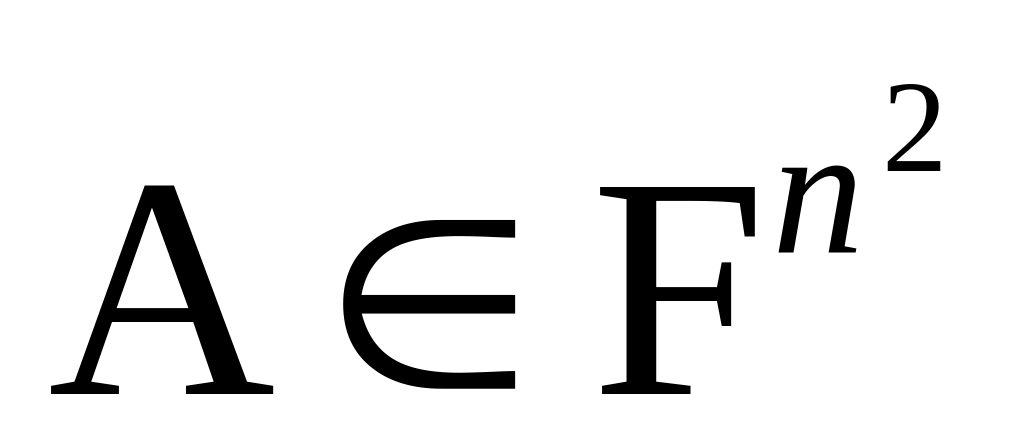 ;
А={A1,A2,…,An};
Ai={ai1,ai2,…,ain}
и обладающей свойством обращаться в
нуль в случае равенства двух каких-либо
векторов-строк:
f(*,X,*,X,*)=0,
где звёздочками отмечены строки с
номерами, i
или j в которых стоят
строки с одинаковыми значениями,
равными Х.
Мы выяснили, что это
свойство эквивалентно кососимметричности
функции f (свойству менять
знак при перестановке любых двух своих
аргументов).
Упражнение 14. Вспомнить
и снова доказать это утверждение.
Как
мы проверяли, для матриц второго и
третьего порядков эта функция, если
ещё добавить к ней нормировочное
требование принимать значение 1 на
единичной матрице, совпадает с
определением определителей для этих
матриц, полученным в п. 2.1 и 2.2. Как нам
ещё докажет это для произвольных матриц
(n-го порядка) Андрей
Кириллович, (последнее, завершающее
конспект «Vector spaces-I»
упражнение 74) эти два условия уже
однозначно, с необходимостью
приводят нас к выражению функции f
через координаты матрицы А=(ai,j)
следующим образом:
f(A)=f(E)
;
А={A1,A2,…,An};
Ai={ai1,ai2,…,ain}
и обладающей свойством обращаться в
нуль в случае равенства двух каких-либо
векторов-строк:
f(*,X,*,X,*)=0,
где звёздочками отмечены строки с
номерами, i
или j в которых стоят
строки с одинаковыми значениями,
равными Х.
Мы выяснили, что это
свойство эквивалентно кососимметричности
функции f (свойству менять
знак при перестановке любых двух своих
аргументов).
Упражнение 14. Вспомнить
и снова доказать это утверждение.
Как
мы проверяли, для матриц второго и
третьего порядков эта функция, если
ещё добавить к ней нормировочное
требование принимать значение 1 на
единичной матрице, совпадает с
определением определителей для этих
матриц, полученным в п. 2.1 и 2.2. Как нам
ещё докажет это для произвольных матриц
(n-го порядка) Андрей
Кириллович, (последнее, завершающее
конспект «Vector spaces-I»
упражнение 74) эти два условия уже
однозначно, с необходимостью
приводят нас к выражению функции f
через координаты матрицы А=(ai,j)
следующим образом:
f(A)=f(E)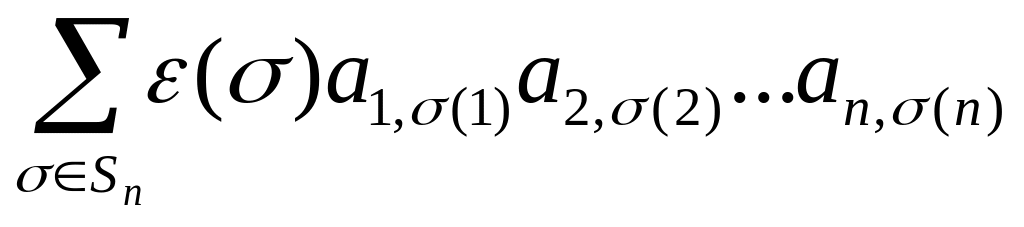 .
(DET1)
Сумма
берётся по всем возможным перестановкам.
В итоге в каждом слагаемом-произведении
n элементов матрицы
представлены одним элементом каждая
строка и каждый столбец. Произведение
входит в алгебраическую сумму со
знаком, равным знаку перестановки .
Добавив сюда естественное нормировочное
условие f(E)=1,
получим новое определение определителя:
Det
A=
(9).
Теперь,
исходя из определения (9), докажите
следующие утверждения.
Упражнение
15.
Det
A – полилинейная функция
на векторах – строках матрицы А (равно
как и на векторах – столбцах этой
матрицы).
Упражнение
16.
Det
A – кососимметрическая
функция на векторах – строках матрицы
А (равно как и на векторах – столбцах
этой матрицы).
Если вспомнить о
комплексных числах, как они у нас
впервые появились, - в виде матриц
второго порядка специального вида, то
модуль комплексного числа совпадает
как раз с определителем его матрицы.
Матрица же сопряжённого комплексного
числа, по модулю равного 1, отличается
от матрицы самого числа тем, что её
коэффициенты получены симметрией
(отражением) относительно главной
диагонали коэффициентов исходной
матрицы. В общем случае, когда имеется
квадратная матрица А=(ai,j)
n-го порядка, сопряжённой
к ней матрицей В=(bi,j)
называется матрица, у которой
.
(DET1)
Сумма
берётся по всем возможным перестановкам.
В итоге в каждом слагаемом-произведении
n элементов матрицы
представлены одним элементом каждая
строка и каждый столбец. Произведение
входит в алгебраическую сумму со
знаком, равным знаку перестановки .
Добавив сюда естественное нормировочное
условие f(E)=1,
получим новое определение определителя:
Det
A=
(9).
Теперь,
исходя из определения (9), докажите
следующие утверждения.
Упражнение
15.
Det
A – полилинейная функция
на векторах – строках матрицы А (равно
как и на векторах – столбцах этой
матрицы).
Упражнение
16.
Det
A – кососимметрическая
функция на векторах – строках матрицы
А (равно как и на векторах – столбцах
этой матрицы).
Если вспомнить о
комплексных числах, как они у нас
впервые появились, - в виде матриц
второго порядка специального вида, то
модуль комплексного числа совпадает
как раз с определителем его матрицы.
Матрица же сопряжённого комплексного
числа, по модулю равного 1, отличается
от матрицы самого числа тем, что её
коэффициенты получены симметрией
(отражением) относительно главной
диагонали коэффициентов исходной
матрицы. В общем случае, когда имеется
квадратная матрица А=(ai,j)
n-го порядка, сопряжённой
к ней матрицей В=(bi,j)
называется матрица, у которой
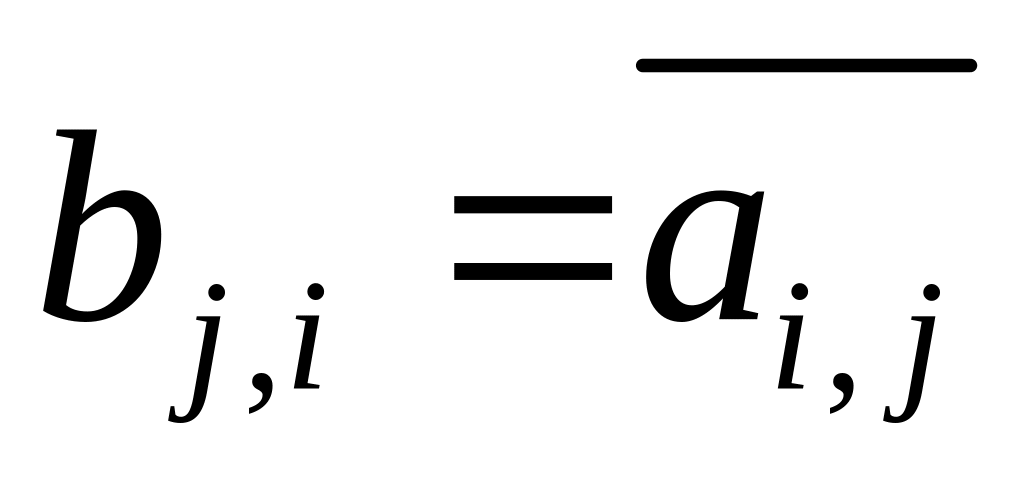 ,
где чёрточка сверху означает комплексное
сопряжение.
Если же коэффициенты
А вещественные, то
,
где чёрточка сверху означает комплексное
сопряжение.
Если же коэффициенты
А вещественные, то
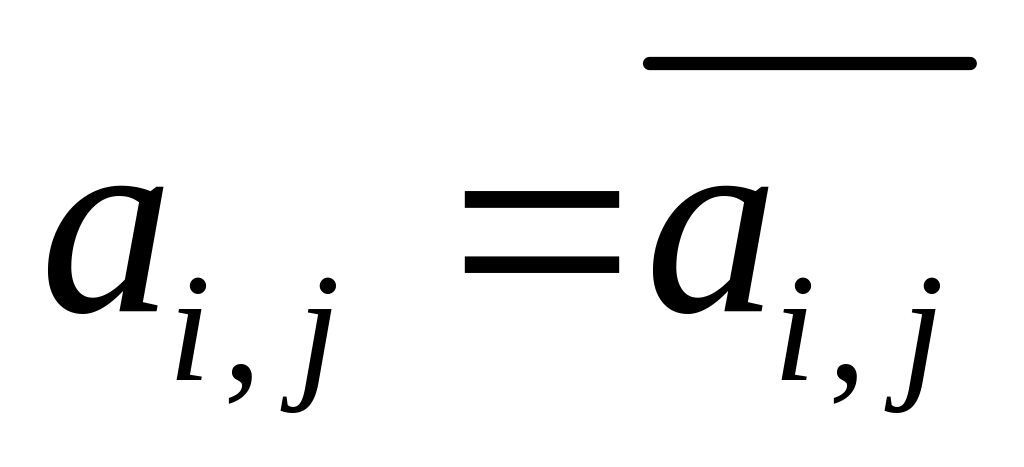 и сопряжённая матрица превращается в
транспонированную
матрицу tA,
столбцы которой являются строками
матрицы А. Учтя, что знак перестановки
и обратной к ней всегда совпадают,
Упражнение 17.
А почему?
докажите, что Упражнение
18. Det
A=Det
tA.
Упражнение
19. Докажите,
что Det Е=1.
Таким
образом, исходя из условий линейности,
кососимметричности и нормировочного
условия det E=1
мы пришли к определению (9). Обратно,
стартуя от определения (9), мы получили
все эти условия.
Упражнение
20.
Определитель
не меняется, если к элементам i-ой
строки матрицы А прибавить элементы
j-ой строки, умноженные
на l.
Упражнение
21.
Определитель
не меняется, если к любой строке матрицы
прибавить линейную комбинацию других
строк.
Упражнение 22.
Если
в матрице А имеется нулевая строка или
столбец, то её определитель равен
нулю.
Упражнение 23.
Если
ранг матрицы меньше n
(т.е., между строками имеется линейная
зависимость), то её определитель равен
нулю.
Упражнение 24.
Определитель
матрицы А и матрицы ВА, где В - унимодулярная
матрица, совпадают.
Упражнение
25.
а)
Если в матрице А имеются две одинаковых
строки, то её определитель равен нулю.
б) Det A=nDet
A.
Def.
Верхнетреугольной
называется матрица, у которой все
компоненты, лежащие ниже главной
диагонали – нулевые:
и сопряжённая матрица превращается в
транспонированную
матрицу tA,
столбцы которой являются строками
матрицы А. Учтя, что знак перестановки
и обратной к ней всегда совпадают,
Упражнение 17.
А почему?
докажите, что Упражнение
18. Det
A=Det
tA.
Упражнение
19. Докажите,
что Det Е=1.
Таким
образом, исходя из условий линейности,
кососимметричности и нормировочного
условия det E=1
мы пришли к определению (9). Обратно,
стартуя от определения (9), мы получили
все эти условия.
Упражнение
20.
Определитель
не меняется, если к элементам i-ой
строки матрицы А прибавить элементы
j-ой строки, умноженные
на l.
Упражнение
21.
Определитель
не меняется, если к любой строке матрицы
прибавить линейную комбинацию других
строк.
Упражнение 22.
Если
в матрице А имеется нулевая строка или
столбец, то её определитель равен
нулю.
Упражнение 23.
Если
ранг матрицы меньше n
(т.е., между строками имеется линейная
зависимость), то её определитель равен
нулю.
Упражнение 24.
Определитель
матрицы А и матрицы ВА, где В - унимодулярная
матрица, совпадают.
Упражнение
25.
а)
Если в матрице А имеются две одинаковых
строки, то её определитель равен нулю.
б) Det A=nDet
A.
Def.
Верхнетреугольной
называется матрица, у которой все
компоненты, лежащие ниже главной
диагонали – нулевые:
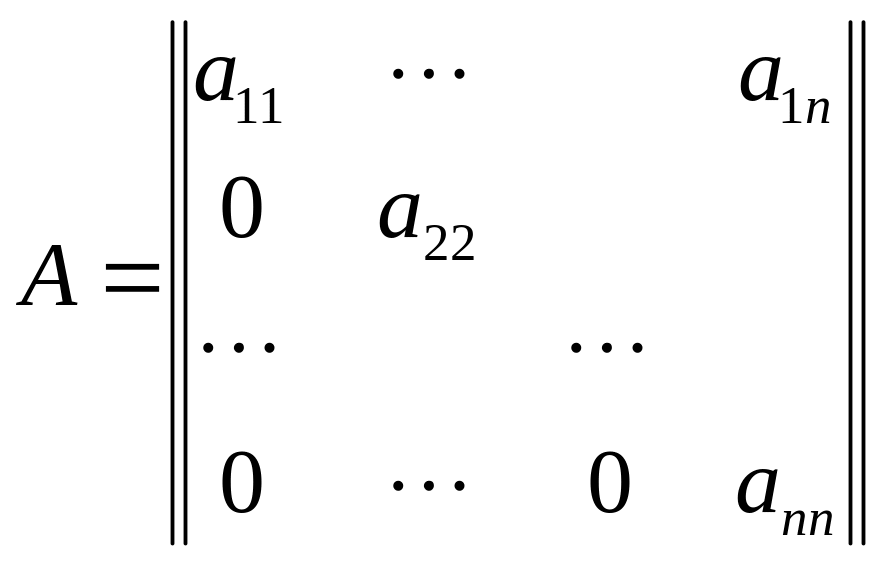 .
.
Упражнение 26.
Докажите, что определитель такой
матрицы равен произведению её компонент,
стоящих на главной диагонали: Det
A=a11a22…ann.
Упражнение
27.
Запишите
в виде определителя третьего порядка
кососимметрическую функцию f:R3R,
f(x,y,z)=(y-x)(z-x)(z-y).
Упражнение
28.
Вычислить
определитель матрицы А=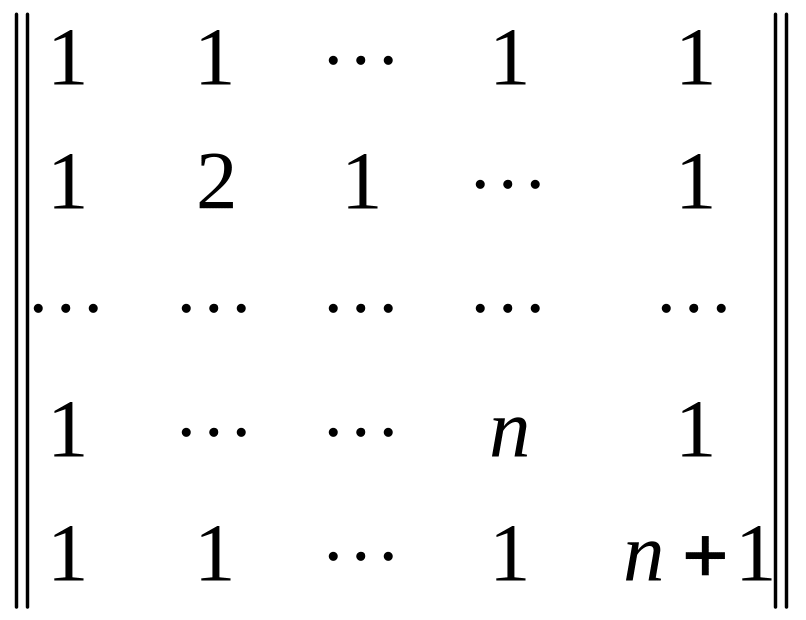 .
Упражнение
29*.
(Формулы
разложения определителя по элементам
столбцов и строк)
Докажите
справедливость следующих формул (ср. с
упр. 11 – только там за определение det
A бралось его разложение
по первому столбцу, а сейчас определением
служит формула 9):
.
Упражнение
29*.
(Формулы
разложения определителя по элементам
столбцов и строк)
Докажите
справедливость следующих формул (ср. с
упр. 11 – только там за определение det
A бралось его разложение
по первому столбцу, а сейчас определением
служит формула 9):
![]() где Аi,j=(-1)i+jMi,j
- алгебраическое дополнение элемента
ai,j.
Упражнение
30*. (Определитель
Вандермонда).
Вычислите
определитель
где Аi,j=(-1)i+jMi,j
- алгебраическое дополнение элемента
ai,j.
Упражнение
30*. (Определитель
Вандермонда).
Вычислите
определитель
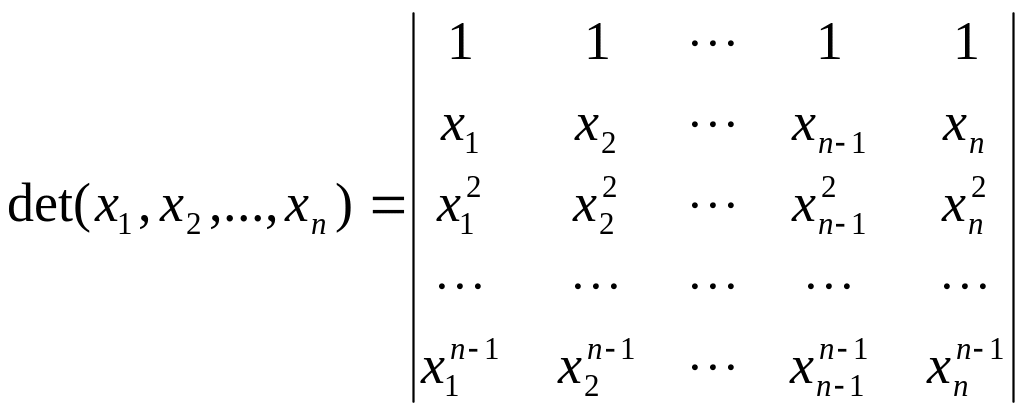 .
(hint:
use properties of a det as a function of columns, notice that it is a
homogeneous polynomial of variables x1,…,xn
of a certain degree and recall the Bezout theorem)
.
(hint:
use properties of a det as a function of columns, notice that it is a
homogeneous polynomial of variables x1,…,xn
of a certain degree and recall the Bezout theorem)
До сих пор мы, давая определения определителю разными способами, доказывали их эквивалентность. Сейчас мы дадим ещё одно определение, в котором за основу берутся следующие свойства, доказанные нами ранее в п. 2.3. Def. Итак, определителем матрицы А с коэффициентами в поле F назовём функцию Det:AF, обладающую следующими свойствами (при этом мы вовсе не можем быть уверены, что функция с такими свойствами вообще существует): а) при умножении любой строки матрицы на элемент поля F определитель её Det тоже умножается на , b) при прибавлении к одной строке матрицы другой её строки значение определителя Det не изменяется, и с) определитель единичной матрицы равен 1: DetE=1. Базируясь теперь на этом, новом определении, докажем заново уже известные ранее нам свойства функции Det (предполагая, что таковая существует): Упражнение 31. Если в матрице имеется нулевая строка, то DetA=0. Упражнение 32. Если к строке Аi матрицы прибавить кратное Аj другой строки, то её определитель DetA не изменится. В развитие этого результата, докажите, что если прибавить к одной строке не только кратное другой строки, но и любую линейную комбинацию других строк, то определитель DetA от этого всё равно не изменится. Упражнение 33. Если у матрицы имеются две одинаковые строки, то её определитель равен нулю. Упражнение 34. Если матрица вырождена, то её определитель равен нулю. Упражнение 35. Если любые две строки матрицы Аi и Аj поменять местами, то значение определителя поменяет знак (он умножится на -1). Упражнение 36. Определитель матрицы не меняется при умножении её слева на унимодулярную матрицу В. Упражнение 37. Определитель же матрицы D() равен (определение матрицы D() см. в п. 1.2). Упражнение 38. Для любых матриц А и В имеет место Det(AB)=DetADetB. Это означает, что Det является гомоморфизмом мультипликативной группы обратимых матриц в мультипликативную группу F* поля F. Итак, Det является полилинейной и кососимметрической функцией строк , нормированной условием DetE=1. То есть, приходим снова к определению, привёдшему к формуле (9). Упражнение 39. Если определитель матрицы равен нулю, то матрица – вырожденная (утверждение, обратное утверждению 34). Если же матрица А невырожденная, то Det (A-1)=(DetA)-1. Итак, критерием вырожденности матрицы является равенство нулю её определителя. Матрица А вырождена DetA=0. Упражнение 40. Функция Det является сюръективным гомоморфизмом GL(n,F)F*; kerDet=SL(n,F). Упражнение 41. Пусть матрица А имеет вид
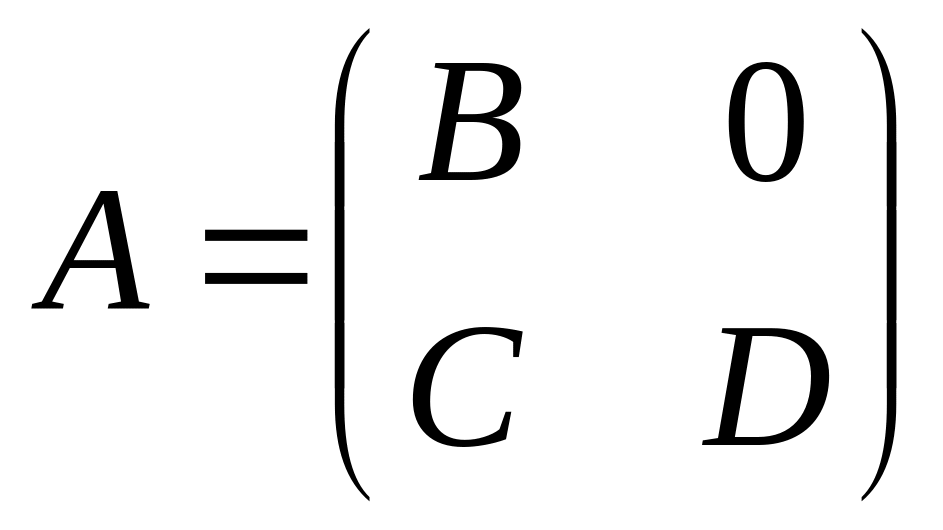 ,
где В и D –квадратные
матрицы. Тогда DetA=DetBDetD.
Упражнение
42.
Определитель
является инвариантом линейного
оператора L: EE
(dimE=n), он
не зависит от выбора базиса, в котором
записана матрица А этого оператора
(хотя сама-то матрица, как мы знаем, от
выбора базиса очень даже зависит!).
Упражнение
43*.
Обозначим алгебру (квадратных)
матриц порядка n над
полем F как M(n,F).
Пусть Аi,j
по-прежнему, обозначает алгебраическое
дополнение к элементу ai,j
матрицы АM(n,F).
Тогда
имеют место
тождества:
ai1Aj1+ai2Aj2+…+ainAjn=ijDetA;
a1iA1j+a2iA2j+…+aniAnj=ijDetA.
(hint:
when i=j ij=1and
we have ex.11. When i≠j ij=0
and we have the decomposition along its jth
row of a matrix, got from original matrix A by replacing its jth
row with its ith
row)
Def.
Матрицу
,
где В и D –квадратные
матрицы. Тогда DetA=DetBDetD.
Упражнение
42.
Определитель
является инвариантом линейного
оператора L: EE
(dimE=n), он
не зависит от выбора базиса, в котором
записана матрица А этого оператора
(хотя сама-то матрица, как мы знаем, от
выбора базиса очень даже зависит!).
Упражнение
43*.
Обозначим алгебру (квадратных)
матриц порядка n над
полем F как M(n,F).
Пусть Аi,j
по-прежнему, обозначает алгебраическое
дополнение к элементу ai,j
матрицы АM(n,F).
Тогда
имеют место
тождества:
ai1Aj1+ai2Aj2+…+ainAjn=ijDetA;
a1iA1j+a2iA2j+…+aniAnj=ijDetA.
(hint:
when i=j ij=1and
we have ex.11. When i≠j ij=0
and we have the decomposition along its jth
row of a matrix, got from original matrix A by replacing its jth
row with its ith
row)
Def.
Матрицу
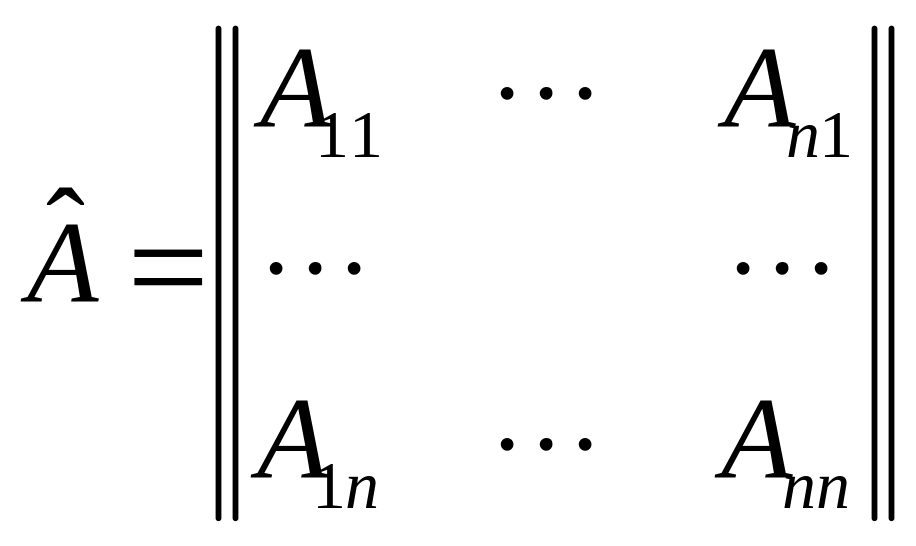 полученную из матрицы А заменой её
элементов ai,j
на алгебраические дополнения Аj,i
к транспонированным элементам aj,i
назовём присоединённой
или взаимной
матрицей к матрице А.
То есть мы сначала транспонируем
матрицу А, а затем заменяем её элементы
на алгебраические дополнения к ним.
Или, наоборот (всё равно), сначала
заменяем, а потом транспонируем.
Упражнение
44*. А-1=(DetA)-1
полученную из матрицы А заменой её
элементов ai,j
на алгебраические дополнения Аj,i
к транспонированным элементам aj,i
назовём присоединённой
или взаимной
матрицей к матрице А.
То есть мы сначала транспонируем
матрицу А, а затем заменяем её элементы
на алгебраические дополнения к ним.
Или, наоборот (всё равно), сначала
заменяем, а потом транспонируем.
Упражнение
44*. А-1=(DetA)-1 Теперь
мы можем обобщить формулы (8) на линейные
системы любого порядка.
Упражнение
45*. (Крамер)
Если Det
(ai,j)≠0,
то единственное решение линейной
системы
Теперь
мы можем обобщить формулы (8) на линейные
системы любого порядка.
Упражнение
45*. (Крамер)
Если Det
(ai,j)≠0,
то единственное решение линейной
системы
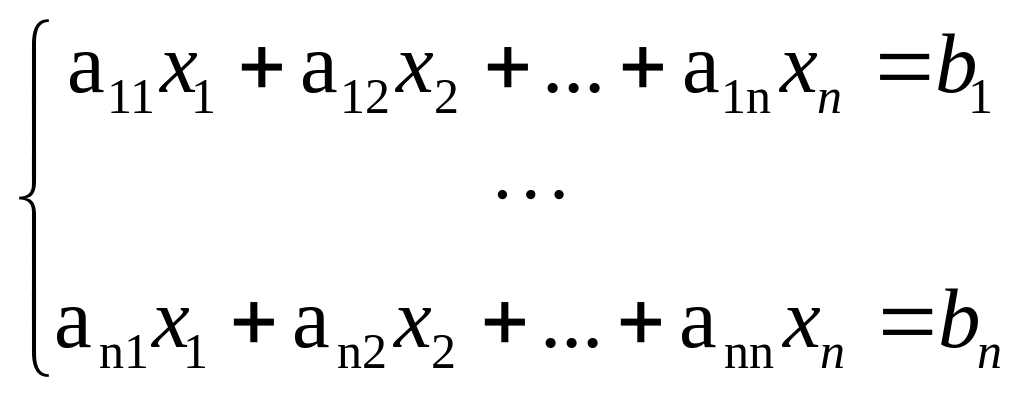 (11)
задаётся формулами
(11)
задаётся формулами
 ,
где определитель в числителе
получается заменой k-го
столбца матрицы А=(ai,j)
столбцом правых частей уравнения (11).
,
где определитель в числителе
получается заменой k-го
столбца матрицы А=(ai,j)
столбцом правых частей уравнения (11).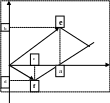 Как
мы с вами проверяли, при n=2,
определитель
Как
мы с вами проверяли, при n=2,
определитель совпадает с точностью до знака с
площадью параллелограмма, построенного
на векторах е=(a,b)
и f=(c,d):
Чтобы снять оговорку «с точностью
до знака», введём понятие ориентированных
длины, площади, объёма и т.д.
Например длиной отрезка АВ, если на
прямой, где расположены точки А и В,
положительное направление совпадает
с лучом АВ, будет обычная длина
АВотрезка
АВ; если на координатной прямой точки
А и В имели координаты соответственно
х и у, то АВ=у-х.
Тогда ориентированной длиной
отрезка ВА будет величина -АВ,
т.е., х-у. Аналогично, ориентированные
площади треугольников АВС и СВА будут
отличаться знаками – они обходятся в
противоположных направлениях (по и
против часовой стрелки).
совпадает с точностью до знака с
площадью параллелограмма, построенного
на векторах е=(a,b)
и f=(c,d):
Чтобы снять оговорку «с точностью
до знака», введём понятие ориентированных
длины, площади, объёма и т.д.
Например длиной отрезка АВ, если на
прямой, где расположены точки А и В,
положительное направление совпадает
с лучом АВ, будет обычная длина
АВотрезка
АВ; если на координатной прямой точки
А и В имели координаты соответственно
х и у, то АВ=у-х.
Тогда ориентированной длиной
отрезка ВА будет величина -АВ,
т.е., х-у. Аналогично, ориентированные
площади треугольников АВС и СВА будут
отличаться знаками – они обходятся в
противоположных направлениях (по и
против часовой стрелки).

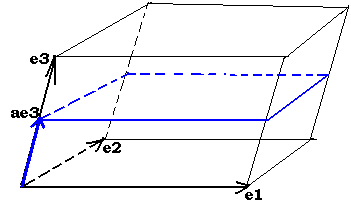 Основными свойствами ориентированного
объёма (в двумерном случае – площади и
в одномерном случае – длины) являются
следующие:
а) если один из векторов
еi, на которые натянут
n-мерный параллелепипед,
изменить в раз
(вытянуть, сжать, возможно, при этом ещё
и обратить – если <0),
оставив все остальные векторы-рёбра
без изменения, то объём измениться в
раз: V2=V1;
б)
если к одному векторов еi,
на которые натянут n-мерный
параллелепипед, прибавить коллинеарный
ему вектор fi
(ибо все остальные векторы-рёбра должны
сохраниться без изменения), то объём
нового параллелепипеда равняется сумме
объёмов старого параллелепипеда и
параллелепипеда, построенного на рёбрах
(e1,e2,…,fi,…,en);
в)
при любой транспозиции векторов-рёбер
параллелепипеда его ориентированный
объём меняет знак на противоположный.
Отсюда следует, что signV
Основными свойствами ориентированного
объёма (в двумерном случае – площади и
в одномерном случае – длины) являются
следующие:
а) если один из векторов
еi, на которые натянут
n-мерный параллелепипед,
изменить в раз
(вытянуть, сжать, возможно, при этом ещё
и обратить – если <0),
оставив все остальные векторы-рёбра
без изменения, то объём измениться в
раз: V2=V1;
б)
если к одному векторов еi,
на которые натянут n-мерный
параллелепипед, прибавить коллинеарный
ему вектор fi
(ибо все остальные векторы-рёбра должны
сохраниться без изменения), то объём
нового параллелепипеда равняется сумме
объёмов старого параллелепипеда и
параллелепипеда, построенного на рёбрах
(e1,e2,…,fi,…,en);
в)
при любой транспозиции векторов-рёбер
параллелепипеда его ориентированный
объём меняет знак на противоположный.
Отсюда следует, что signV![]() =(),
где
=(),
где
 .
Как
мы видим, ориентированный объём
параллелепипеда является линейной и
кососимметрической функцией от векторов,
на которых, как на рёбрах, он построен.
При этом достаточно лишь добавить
естественное требование, чтобы объём
единичного параллелепипеда (т.е.
построенного на единичных векторах –
векторах стандартного базиса) был равен
1 и мы вновь приходим вновь к одному из
исходных определений определителя.
.
Как
мы видим, ориентированный объём
параллелепипеда является линейной и
кососимметрической функцией от векторов,
на которых, как на рёбрах, он построен.
При этом достаточно лишь добавить
естественное требование, чтобы объём
единичного параллелепипеда (т.е.
построенного на единичных векторах –
векторах стандартного базиса) был равен
1 и мы вновь приходим вновь к одному из
исходных определений определителя.
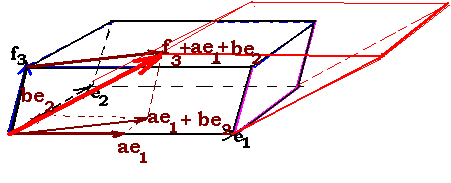
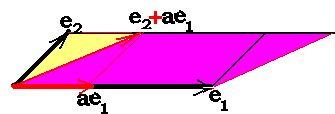 Между прочим, условие «ориентированный
объём не меняется при добавлении к
вектору кратного любого другого вектора»
тоже легко иллюстрируется – в двумерном
случае это равносоставленность
параллелограммов с общими основаниями
и высотами, в трёхмерном – соответственно,
таких же параллелепипедов.
Итак,
мы приходим к выводу, что ориентированный
объём параллелепипеда, построенного
на векторах, как на рёбрах, совпадает с
определителем матрицы, строками которой
являются координаты этих векторов.
Площадью любой фигуры является число
клеточек-квадратиков (соответственно,
кубиков и т
Между прочим, условие «ориентированный
объём не меняется при добавлении к
вектору кратного любого другого вектора»
тоже легко иллюстрируется – в двумерном
случае это равносоставленность
параллелограммов с общими основаниями
и высотами, в трёхмерном – соответственно,
таких же параллелепипедов.
Итак,
мы приходим к выводу, что ориентированный
объём параллелепипеда, построенного
на векторах, как на рёбрах, совпадает с
определителем матрицы, строками которой
являются координаты этих векторов.
Площадью любой фигуры является число
клеточек-квадратиков (соответственно,
кубиков и т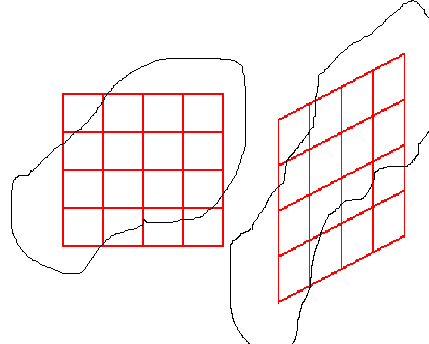 .д.),
расположенных внутри этой фигуры (при
увеличении частоты сетки – уменьшении
размеров клеточек их сумма «стремится»
к истинному значению «площади фигуры»
- ничего более точного и определённого
в этом отношении мы пока сказать не
можем). Число узлов клетки внутри фигуры
не меняется при любом линейном
невырожденном преобразовании, площадь
же каждой клеточки при этом изменяется
пропорционально с одним и тем же
коэффициентом, равным определителю
этого преобразования. Таким образом,
определитель линейного преобразования
ВП V отвечает не только
за то, во сколько раз изменится объём
параллелепипедов в V, а
во сколько раз вообще изменится объём
любой фигуры в V.
Познакомимся
ещё с одним инвариантом линейного
преобразования f: VV.
Def.
Следом
(trace)
матрицы А называется сумма её
диагональных элементов:
.д.),
расположенных внутри этой фигуры (при
увеличении частоты сетки – уменьшении
размеров клеточек их сумма «стремится»
к истинному значению «площади фигуры»
- ничего более точного и определённого
в этом отношении мы пока сказать не
можем). Число узлов клетки внутри фигуры
не меняется при любом линейном
невырожденном преобразовании, площадь
же каждой клеточки при этом изменяется
пропорционально с одним и тем же
коэффициентом, равным определителю
этого преобразования. Таким образом,
определитель линейного преобразования
ВП V отвечает не только
за то, во сколько раз изменится объём
параллелепипедов в V, а
во сколько раз вообще изменится объём
любой фигуры в V.
Познакомимся
ещё с одним инвариантом линейного
преобразования f: VV.
Def.
Следом
(trace)
матрицы А называется сумма её
диагональных элементов:
![]() .
Пусть
прямоугольные матрицы А и В таковы, что
определено как АВ, так и ВА (для этого
необходимо и достаточно, чтобы одна из
них имела размеры mn,
а другая - nm).
Тогда обе матрицы АВ и ВА – квадратные
(одна – порядка m, а другая
- порядка n) и потому для
обеих определена функция tr.
Упражнение
46.
Докажите, что tr
AB=tr
BA.
Выведите
отсюда, что след является характеристикой
(инвариантом) линейного оператора и не
зависит от базиса, в котором записан
этот оператор:
Упражнение 47.
Пусть
f: VV
линеен и в базисе е записан матрицей
А, а в базисе f –
матрицей B.
Тогда tr
A=tr B.
Таким образом, можно говорить о следе
tr f
оператора
f.
.
Пусть
прямоугольные матрицы А и В таковы, что
определено как АВ, так и ВА (для этого
необходимо и достаточно, чтобы одна из
них имела размеры mn,
а другая - nm).
Тогда обе матрицы АВ и ВА – квадратные
(одна – порядка m, а другая
- порядка n) и потому для
обеих определена функция tr.
Упражнение
46.
Докажите, что tr
AB=tr
BA.
Выведите
отсюда, что след является характеристикой
(инвариантом) линейного оператора и не
зависит от базиса, в котором записан
этот оператор:
Упражнение 47.
Пусть
f: VV
линеен и в базисе е записан матрицей
А, а в базисе f –
матрицей B.
Тогда tr
A=tr B.
Таким образом, можно говорить о следе
tr f
оператора
f.
