Методика решения задач

Задача 1. Бесконечно большая пластина из одномерного диэлектрика с проницаемостью заряжена равномерно сторонним зарядом с объемной плотностью >0. Толщина пластины 2а. Найти:

1) модуль вектора и потенциал как функции расстояния от середины пластины (потенциал в середине пластины положить равным нулю); взяв координатную ось X перпендикулярно пластине, изобразить примерные графики зависимостей проекции Е_х(х) вектора и потенциала ;

2. поверхностную и объемную плотности связанного заряда.

Решение . 1) Из соображений симметрии ясно, что в середине пластины Е=0, а во всех остальных точках вектор перпендикулярен поверхности пластины. Для определения воспользуемся теоремой Гаусса для вектора (ибо нам известно распределение только сторонних зарядов). Возьмем в качестве замкнутой поверхности прямой цилиндр высотой l, один торец которого совпадает со средней плоскостью пластины. Пусть площадь сечения этого цилиндра равна S, тогда

г рафики функций Е_х(х) и показаны на рисунке 1.

Рисунок 1. Графики функций Е_х(х) и .

2) Поверхностная плотность связанного заряда

Этот результат справедлив для обеих поверхностей пластины. Таким образом, если сторонний заряд >0, то на обеих поверхностях пластины выступит также положительный связанный заряд. Для определения объемной плотности связанного заряда воспользуемся формулой:

Отсюда видно, что связанный заряд распределен по объему равномерно и имеет знак, противоположный стороннему заряду.

Задача 2. Однородный диэлектрик имеет вид сферического слоя, внутренний и внешний радиусы которого равны a и b. Изобразить примерные графики напряженности Е и потенциала электрического поля как функции расстояния r от центра системы, если диэлектрику сообщили положительный сторонний заряд, распределенный равномерно: 1) по внутренней поверхности слоя; 2) по объему слоя.

Решение 1) Воспользуемся теоремой Гаусса для вектора , взяв в качестве замкнутой поверхности сферу радиусом r:

где q — сторонний заряд внутри этой сферы. отсюда следует, что

Искомая напряженность

Г рафик зависимости E(r) показан на рисунке 2,а. На этом же рисунке изображен и график зависимости от r. График должен иметь такой вид,

Рисунок 2. Графики зависимостей Е® и .

Чтобы производная , взятая с обратным знаком, соответствовала графику функции Е®.

При этом должно быть учтено и условие нормировки: при .

Следует обратить внимание на то, что график является непрерывным. В местах конечных разрывов функции Е® график испытывает лишь изломы.

2) В данном случае согласно теореме Гаусса

где - объемная плотность стороннего заряда. Отсюда

.

Соответствующие графики зависимостей E® и показаны на рисунке 2,б.

Задача 3.Сторонние заряды равномерно распределены с объемной плотностью по шару радиусом а из однородного диэлектрика с проницаемостью . Найти модуль вектора как функцию расстояния r от центра шара, изобразить примерные графики функции E® и потенциала.

Решение Для определения воспользуемся теоремой Гаусса для вектора , поскольку задано распределение лишь сторонних зарядов:

Р исунок 3. График функций E® и .

.

График функции E® и показан на рисунке 3.

Задача 4. Найти емкость шарового проводника радиусом а, окруженного примыкающим к нему слоем однородного диэлектрика с наружным радиусом b и проницаемостью . Изобразить примерные графики зависимостей поля E® и потенциала , где r – расстояние от центра до шара, если проводник заряжен положительно.

Решение. По определению емкость . Найдем потенциал проводника, мысленно сообщив ему заряд q:

.

После интегрирования этого выражения получим:

.

Графики зависимостей E® и показаны на рисунке 4.

Рисунок 4. Графики зависимостей E® и .

Задача 5. Сферический конденсатор с радиусами обкладок a и b, где a<b , заполнен изотропным, но неоднородным диэлектриком, проницаемость которого зависит от расстояния r до центра системы как , – постоянная. Найти емкость такого конденсатора.

Решение. Согласно определению емкости конденсатора (C=q/U) задача сводится к нахождению разности потенциала U при заданном заряде q:

, (1)

где предполагается, что внутренняя обкладка имеет заряд q>0. Определим с помощью теоремы Гаусса для вектора :

.

После подстановки последнего выражения в (1) и соответствующего интегрирования найдем:

.

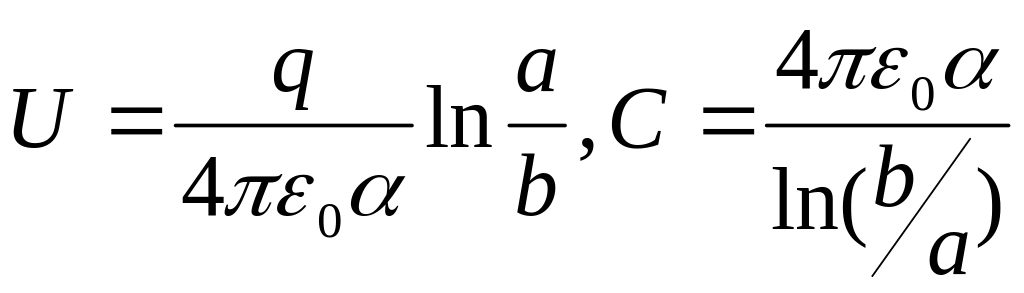Задача 6. По тонкой нити, изогнутой по дуге окружности радиусом R₁ равномерно распределен заряд с линейной плотностью . Определить потенциал электростатического поля в точке, совпадающей с центром кривизны дуги. Длина нити l составляет 1/3 длины окружности.

Решение. Так как заряженную дугу в условиях данной задачи нельзя считать точечным зарядом, то воспользоваться формулой для потенциала поля точечного заряда мы не можем. Поэтому разобьем заряженную дугу на участки, заряды которых (dl<<R) можно считать точечными.

Заряд дуги размера dl

,

Потенциал поля такого заряда в точке О (в центре окружности)

По принципу суперпозиции электрических полей

Т.к l составляет длины дуги окружности, то

Подставляя численные данные, получаем .

Задача 7. Точечный заряд Q=1нКл помещен в центре куба со стороной а=1м. Чему равен поток вектора напряженности электрического поля через одну грань куба?

Решение. Т.к. поверхность куба является замкнутой, то поток через всю поверхность можно найти по теореме Гаусса для напряженности электрического поля в вакууме

,

где - электрическая постоянная

В силу симметрии поверхности и расположения заряда в центре куба поток через все грани будет одинаковым. Т.к у куба 6 граней, то

.