6. Классификация элементарных функций.

Функции построенные из основных элементарных функций с помощью конечного числа алгебраических действий называются элементарными.

1.Степенная функция

2. Показательная функция , где , и

3.Тригонометрическая функция

4. Обратные тригонометрические функции

5.Логарифмические функции у = log_ах, а>0, а ≠ 1

7. Предел функции. Теоремы о пределах.3амечательные пределы.

Определение. Число b называется пределом функции f(x) при x→a, если, по мере того, как x приближается к а – будь то справа или слева, - значение f(x) неограниченно приближается к b.

Основные теоремы .

1. Предел суммы двух функций равен сумме пределов. lim (f(x) + φ(x)) = lim f(x) + lim φ(x)

2. Предел произведения двух функций равен произведению пределов. lim [f(x) * φ(x)] = lim f(x) * lim φ(x)

3. Предел произведения числа на функцию равен произведению числа на предел функции. lim С*f(x) = С *lim f(x)

4. Предел отношения двух функций равен отношению пределов этих функций. (Кроме случая, когда знаменатель стремиться к нулю). lim f(x) / φ(x) = lim f(x) / lim φ(x), limφ(х)≠0. Если знаменатель стремиться к нулю, а числитель - нет, то говорят, что отношение стремиться к бесконечности.

Замечательные пределы.

1. lim sin(x)/х = 1, при х→0

2. lim (1+1/х)^х = ℮, при х→0

3. lim (1+х)^1/х = ℮, при х→0

4. lim tg(x)/х = 1, при х→0

5. lim ln(1+x)/х = 1, при х→0

6. lim (1/х) = 0, при х→ ∞

(a/∞→0; a/0→∞; ∞/1→∞)

8. Односторонние пределы. Несобственные пределы.

Односторонний предел - предел функции в некоторой точке справа или слева.

Если значение функции f(x)стремится к числу b по мере стремления x к a со стороны меньших значений, то число b называют левосторонним пределом функции f(x) в точке x →a и пишут:

Если значение функции f(x)стремится к числу b по мере стремления x к a со стороны больших значений, то число b называют правосторонним пределом функции f(x) в точке x→a и пишут:

Несобственные пределы –

9. Непрерывность функции в точке.

Функция f(x) называется непрерывной в точке х₀, если предел функции и ее значение в этой точке равны, т. е.

10. Непрерывность функции в интервале. Действия с непрерывными функциями.

Функция f(x) непрерывна в интервале (а, b), если она непрерывна в каждой точке этого интервала; непрерывна на отрезке [а, b], если она непрерывна в интервале (а, b) и непрерывна в точке x=а справа, а в точке x=b слева, т. е. и .

Действия с непрерывными функциями.

1. Сумма, разность и произведение двух функций f(x) и g(x), непрерывных в точке х=а, непрерывны в этой точке. f(x) ±g(x), f(x)*g(x) и f(x)/g(x)

2. Если функция f(x) непрерывна при некотором значении х, то приращение функции бесконечно мало при бесконечно малом приращении аргумента.

11. Разрывы функций. Классификация разрывов.

Точки, где функция f(x) не является непрерывной, называются точками разрыва функции f(x).

1. Устранимый разрыв. Он имеет место, когда выполнено условие

2. Точка х₀ называется точкой разрыва первого рода функции f(x), если в этой точке функция f(x) имеет конечные, но не равные друг другу правый и левый пределы.

3. Точка х₀ называется точкой разрыва второго рода функции f(x), если в этой точке функция f(x) не имеет, по крайней мере, одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.

12. Производная функции. Геометрический смысл производной.

Производная - предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную, называют дифференцируемой. .

Геометрический смысл производной состоит в том, что численно она равна тангенсу угла между касательной, проведенной к кривой в точке x, и осью абсцисс OX.

1З. Теоремы о производной суммы, произведения и частного.

Сумма, разность. Производная суммы равна сумме производных

Произведение.

Частное.

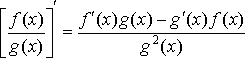
74. Производная сложной и обратной функции. Понятие о логарифмической производной.

Сложной ф-ии:

Обратной ф-ии:

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм, а затем вычисляется производная от него.

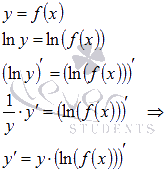
15. Дифференциал, связь дифференциала и приращения функции.

Для того, чтобы функция f(x) была дифференцируемой в точке х, необходимо и достаточно, чтобы она имела производную в этой точке.

Производная есть отношение дифференциала функции к дифференциалу независимой переменной. → df(x) = f’ * dx

Функция f(x) называется дифференцируемой в точке х, если ее приращение может быть представлено в виде

Линейная часть приращения функции, то есть слагаемое называется дифференциалом функции в точке х и обозначается так: .