31. Биномиальный интеграл.

Неопределенные интегралы иррациональных функций вида находятся методом подстановки.

В зависимости от рациональных чисел m, n и p вводят следующие новые переменные:

1) Если p - целое число, то принимают , где N - общий знаменатель чисел m и n.

2) Если - целое число, то , где N - знаменатель числа p.

3) Если - целое число, то вводят новую переменную , где N - знаменатель числа p.

З2. Интегрирование функции R(sinx, cosx).

33. Интегрирование функции , а>0.(1-я подстановка Эйлера).

Подстановка Эйлера - замена переменной х=x(t) в интеграле.

34. Интегрирование функции , с>О. .(2-я подстановка Эйлера).

35. Интегрирование функции , b>0. (З-я подстановка Эйлера).

36. Понятие определенного интеграла.

Если существует конечный предел I интегральной суммы при λ→0, и он не зависит от способа выбора точек ξ _i, способа разбиения отрезка, то этот предел называется определенным интегралом от функции f(x )по отрезку [a,b] и обозначается следующим образом: , или .

37. Основные свойства определенного интеграла.

1) Определённый интеграл численно равен площади криволинейной трапеции, ограниченной графиком функции у=f(x), осью абсцисс, и прямыми х=а, х=b.

2) Если нижний и верхний пределы интегрирования поменять местами, то значение определённого интеграла изменится на противоположное .

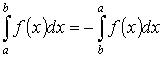3) Если промежуток интегрирования стянут в точку, фигура под кривой стягивается в отрезок, площадь которого равна нулю .

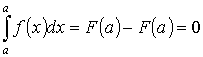4) Постоянный множитель можно выносить за знак интеграла .

5) Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций: .

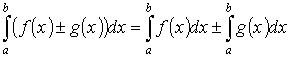6) Если промежуток интегрирования разбит на части, то интеграл по всему отрезку равен сумме интегралов по каждой части. .

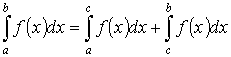7) Если на отрезке [a, b], где а < b, имеет место неравенство 0 ≤ f (x) ≤ g (x), то .

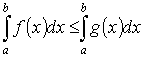8) Теорема о среднем. Если функция y = f (x) непрерывна на отрезке [a, b], где а < b, то найдется такое значение c є [a, b], что .

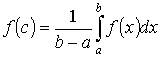38. Основные условия интегрируемости функций.

1) Если функция f (x) интегрируема на отрезке [a, b], то она ограничена на этом отрезке.

2) Для того чтобы ограниченная на отрезке [a, b] функция f (x) была интегрируемой на этом отрезке, необходимо и достаточно, чтобы . (S и s – суммы Дарбу)

39. Связь определенного интеграла с первообразной.

Формула Ньютона - Лейбница устанавливает связь между определённым интегралом от данной функции и первообразной для этой функции, то есть между определённым и неопределённым интегралами.

40. Формула Ньютона-Лейбница.

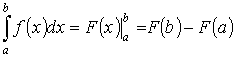
41. 3амена переменной в определенном интеграле.

Пусть функция φ (t) имеет непрерывную производную на отрезке [α, β], а = φ (α), b = φ (β) и функция f (x) непрерывна в каждой точке x = φ (t), где t є [α, β]. Тогда справедливо равенство

Использование замены переменной позволяет упростить интеграл, приблизив его к «табличному». При этом в отличие от неопределенного интеграла, в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t из уравнений φ (t) = a и φ (t) = b.

42. Вычисление определенного интеграла по частям.

43. Вычисление площади плоской фигуры.

Пусть на плоскости Оху дана фигура, ограниченная отрезком [а, b] оси Ох, прямыми х = а, х = b и графиком непрерывной и неотрицательной функции y = f ( x) на [ а, b]. Такую фигуру называют криволинейной трапецией и площадь её можно вычислить по формуле .

44. Вычисление объема тела вращения.

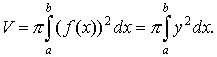
45. Вычисление длины дуги плоской кривой.

46. Вычисление площади поверхности тела вращения.

47. Среднее значение функции. Интегральная теорема о среднем.

Среднее значение функции — это некоторое число, заключённое между наименьшим и наибольшим её значениями.

Теорема о среднем. Если функция y = f (x) непрерывна на отрезке [a, b], где а < b, то найдется такое значение c є [a, b], что .

48. Интегрирование функций, неопределенных в конечном числе точек.

Пусть функция y = f(x) определена и интегрируема на произвольном отрезке [а, t], т.е. функция определена для произвольного значения t ≥ a. Несобственным интегралом (интегралом первого рода) от функции f(x) на полуинтервале [а, +∞) называется предел Если предел, стоящий в правой части равенства, существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), в противном случае — расходящимся.

Выделяют следующие две задачи:

а) исследование вопроса о сходимости заданного несобственного интеграла;

б) вычисление значения интеграла в случае, если несобственный интеграл сходится.

В некоторых случаях решения этих двух задач удается объединить.

По аналогии с определяется несобственный интеграл на полуинтервале (-∞, b]: 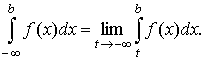Определение сходимости интеграла аналогично приведенному выше.