49. Интегрирование функций, имеющих разрывы второго рода.

Пусть на полуинтервале задана функция , интегрируемая на любом отрезке , где , однако не интегрируемая на отрезке . В точке b эта функция может быть вовсе не определена и стремиться к ∞ при , любо вовсе не иметь никакого предела при этой базе. Рассмотрим функцию она определена при . Эта функция может иметь предел при (левосторонний предел). Этот предел мы будем называть значением интеграла от f(x) по всему полуинтервалу и обозначать в точности как обычный интеграл: .

Пусть функция f(x) удовлетворяет указанным выше условиям на . Несобственным интегралом второго рода назовём тогда интеграл , значение I которого равняется левостороннему пределу

Если этот предел существует, то несобственный интеграл называется сходящимся, а если предела не существует, то расходящимся. Расходящемуся интегралу не приписывается никакого числового значения; в этом случае будем условно писать

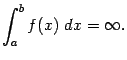
50. Интегрирование функций, заданных на бесконечном интервале.

Несобственный интеграл на интервале (-∞ , +∞) определяется следующим образом

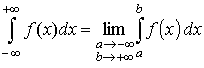
Интеграл называется сходящимся, если существует конечный предел справа как предел функции двух переменных. Если предела нет, то несобственный интеграл называется расходящимся.

51. Понятие функции нескольких переменных.

Переменная z называется функцией нескольких независимых переменных в множестве М, если каждому набору чисел из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z

52. Области открытые и замкнутые. Граница области.

Область, состоящую из одних внутренних точек, мы будем называть открытой или незамкнутой. Если же к области относятся еще и точки границы, то область называют замкнутой.

Точки сгущения для открытой области, не принадлежащие ей, называются пограничными точками этой области. Пограничные точки в их совокупности образуют границу области.

53. Сечения и линии уровня функции нескольких переменных.

Линией уровня функции z=f(x;y) называется линия f(x;y)=C на плоскости XOY, в точках которой функция сохраняет постоянное значение z=C. (Линией уровня функции z=f(x,y) называется линия на плоскости Oxy, в точках которой функция сохраняет постоянное значение.)

Пересечение S∩P является плоской кривой, которая называется сечением поверхности S плоскостью P. (S – некоторая поверхность, P - плоскость)

54. Непрерывность функций нескольких переменных.

Функция f(x) называется непрерывной в точке x₀, если

55. Свойства непрерывных функций нескольких переменных.

1) Если f(x) и g(x) непрерывны в точке x₀, то в этой же точке непрерывны и функции f(x) ± g(x), f(x) × g(x) и f(x)/g(x) (последнее только в случае, если g(x)=0)

2) Теорема о непрерывности сложной функции. Пусть x = j(t) непрерывна в точке t₀, а функция f(x) непрерывна в точке x₀ = j(t₀). Тогда функция y = f(j(t)) непрерывна в точке t₀.

3) Пусть функция f(x) непрерывна на промежутке [a,b] и принимает на его концах значения разных знаков. Тогда на этом промежутке существует такая точка c, в которой f(с)=0.