28. Неявные фнп и их дифференцирование.

Пусть значения двух переменных (x) и (y) связаны между собой некоторым уравнением , которое мы запишем в виде F(x,y)=0      (2-94).   Это есть неявная функция т.к. (y) не выражено явно через (x). Так, например уравнение x²+y²-a²=0 (2-95).

Правило. Дифференцирование неявной функции происходит по правилу нахождения производных, считая (x)-независимой переменной, а (y) – зависимой переменной.

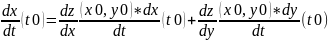
Теорема 2. Пусть функция z = f(x, y) дифференцируема в точке (x₀, y₀) и ее аргументы x = x(u, v) и y = y(u, v) дифференцируемы в точке (u₀, v₀) , причем x(u₀, v₀) = x₀ , y(u₀, v₀) = y₀ .

Тогда сложная функция z = f(x(u, v), y(u, v)) переменных u и v дифференцируема в точке (u₀, v₀) и ее частные производные вычисляются по формулам

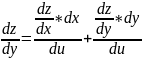
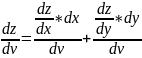
29. Экстремум фнп. Необходимое и достаточные условия экстремума.

Теорема (Необходимое условие экстремума) Если функция нескольких переменных u = f(x₁, x₂, … , x_n) имеет экстремум в некоторой точке, то в этой точке каждая ее частная производная равна нулю или не существует. Внутренние точки из области определения функции, в которых выполняются необходимые

условия экстремума, называются критическими. Если в критической точке функция дифференцируема, то такая точка называется стационарной.

достаточным условием экстремума функции нескольких переменных в ее стационарной точке является знакоопределенность (положительная или отрицательная определенность) дифференциала 2–го порядка в этой точке.

Полная производная функции — производная функции по времени вдоль траектории.

Расчёт полной производной функции   по времени t,   (в отличии от частной производной,  ) не подразумевает, что другие аргументы (т.е. иные нежели аргумент, t, по которому ведётся полное дифференцирование: x и y) постоянны при изменяющемся t. Полная производная включает в себя эти непрямые зависимости от t (т.е. x(t)и y(t)) для описания зависимости f от t.

30. Условный экстремум ФНП. Метод Лагранжа нахождения условного экстремума.

 Условным экстремумом функции z  = f (х, у) называется экстремум этой функции, достигнутый при условии,  что переменные х и у связаны уравнением  (х, у) = 0 (уравнением связи).

Метод множителей Лагранжа. Если уравнение   не разрешимо ни относительно   , ни относительно  , то рассматривают функцию Лагранжа . Необходимым условием существования условного экстремума функции   при условии   является равенство нулю всех частных производных функции Лагранжа:    .

31. Наибольшее и наименьшее значения ФНП в ограниченной замкнутой области.

Теорема 1.5 Пусть в замкнутой области D задана функция z=z(x,y), имеющая непрерывные частные производные первого порядка. Граница Г области D является кусочно гладкой (т. е. состоит из кусков "гладких на ощупь" кривых или прямых). Тогда в области Dфункция z(x,y) достигает своего наибольшего M и наименьшего m значений.

Без доказательства.

Можно предложить следующий план нахождения M и m.  1. Строим чертёж, выделяем все части границы области D и находим все "угловые" точки границы.  2.Находим стационарные точки внутри D.  3. Находим стационарные точки на каждой из границ.  4. Вычисляем во всех стационарных и угловых точках, а затем выбираем наибольшее M и наименьшее m значения. 

32. Скалярное поле и его геометрическое изображение. Поверхности и линии уровня.

Называется часть пространства или всё пространство каждой точки Р которой соответствует численное значение некоторой скалярной величины U.

Поверхностью уровня поля   называют геометрическое место точек, в которых поле принимает постоянное значение. Согласно такому определению, уравнение поверхности уровня будет иметь вид: или

33. Производная по направлению.

производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления. Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.

34. Градиент и его связь с производной по направлению.

Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления: ,где   — орт направления. Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке. Также видно, что значение производной по направлению не зависит от длины вектора  .

35. Касательная плоскость и нормаль к поверхности.

 Касательной плоскостью к поверхности   в данной точке P (x₀, y₀, z₀) называется плоскость, проходящая через точку Р и содержащая в себе все касательные, построенные в точке Р ко всевозможным кривым на этой поверхности, проходящим через точку Р.

Нормалью к поверхности s в точке Р называется прямая, проходящая через точку Р и перпендикулярная к касательной плоскости, построенной в этой точке.

36. Первообразная и неопределенный интеграл. Теорема существования неопределенного

интеграла.

Ф-ция F(х)-первообразная от ф-ции f(х)  если для любого x из области определения f(x) выполняется равенство F'(x)= f(x) или dF(x)= f(x)dx

Неопределенным интегралом (н.и.) от функции называется совокупность всех первообразных этой функции. Обозначение н.и.:

Т.Любая непрерывная ф-ция на отрезке [a;b] f(x)имеет на этом отрезке первообразную F(x) такую что F'(x)= f(x) .Если ф-ия имеет т. Разрыва то её рассматриваю только в тех интервалах где она непрерывна .

37. Свойства неопределенного интеграла.

1) постоянную можно выносить за знак интеграла.

2) интеграл суммы равен сумме интегралов.

3)производная от интеграла равна подынтегральной функции.

4)интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.

38. Основные методы интегрирования: 1непосредственное интегрирование,2 замена

переменных, 3интегрирование по частям.

1)отыскание Н.И. с помощью табл. Интегралов и тождественных преобразований

2)Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует

3) ∫udv=uv-∫vdu- ф-ла интегрирования по частям где u и v дифф. Ф-ция. Данная формула показывает, что интеграл ∫udv приводит к интегралу ∫vdu, который может оказаться более простым, чем исходный, или даже табличным.

39. Интегрирование функций, содержащих квадратный трехчлен.

Интеграл вида , основной приём вычисления привидения квадратного трехчлена к виду (ax^2+bx+c=a(x+k)^2+l )(1)где k и l постоянные для выполнения данного преобразования удобнее выделить полный квадрат можно так же пользоваться подстановкой (2ax+b=t)

Если a=0 то кв. трёхчлен приводим к виду(1) получаем табл. Интегралы.

40. Интегрирование рациональных функций.

для интегрирования рациональной функции  , где P(x) и Q(x) целые многочлены причём степень числителя меньше степени знаменателя .затем Разложение знаменателя на простейшие дроби для вычисление неопределённых коэффициентов обе части тождества приводят к целому виду а затем приравнивают коэффициенты при одинаковых степенях переменной х.

41. Интегрирование тригонометрических функций.

1.Интегралы вида       вычисляются преобразованием произведения тригонометрических функций в сумму по формулам:

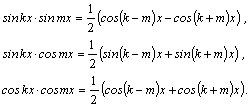
2.Интегралы вида , где m или n– нечетное положительное число, вычисляются подведением под знак дифференциала.

3.Интегралы вида  , где m и n–четные положительные числа, вычисляются с помощью формул понижения степени:

4.Интегралы   где  вычисляются заменой переменной: или

5.Интегралы вида   сводятся к интегралам от рациональных дробей с помощью универсальной тригонометрической подстановки  тогда 

42. Интегрирование некоторых иррациональностей.

Интеграл вида где R рациональная ф-ция где а и у в степени целые числа 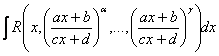 интегралы такого вида находятся с помощью подстановки   где m общее наименьшее кратное чисел

43. Определенный интеграл как предел интегральной суммы и его геометрический смысл.

Пусть на отрезке [a,b] задана функция y = f(x). Разобьём отрезок [a,b] произвольным образом на n частей

Сумма вида Sn= 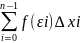-интегральная сумма ф-ции на данном отрезке.

Геометр. смысл Sn представляет собой арифметическую сумму площадей соответствующих прямоугольников .

Предел интегральной суммы если ф-ция непрерывна на [a;b] , то она интегрируема на этом отрезке, т.е. это т предел существует независимо от способа разбиения промежутка интегрирования на части и выбора точек на отрезках.

Геометр смысл сумма площадей фигур составляющие криволинейную трапецию части, которой выше ОХ берутся с «+» а которые ниже ОХ с «-»

44. Свойства определенного интеграла.

I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е.  , где х, t – любые буквы.

II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

V. Постоянный множитель можно выносить за знак определенного интеграла.

VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

45. Интеграл с переменным верхним пределом.

Пусть на отрезке [ a, b ] задана непрерывная функция  f ( x ), тогда для любого x   [ a, b ] существует функция: 

задаваемая  интегралом с переменным верхним пределом, стоящим в правой части равенства.

На интеграл с переменным верхним пределом распространяются все правила и свойства определённого интеграла.

Из определения интеграла с переменным верхним пределом - функции F(x) и известных свойств интеграла следует, что при x   [ a, b ] F' ( x ) = f ( x ) .

46. Формула Ньютона – Лейбница.

Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.

Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).

47. Замена переменных в определенном интеграле.

Если ф-ция f(x) непрерывна на отрезке a≤x≤β и x=ф(t)–функция непрерывна вместе со своей производной

ф(t) на отрезке α ≤t≤β где a=ф(α) и b =ф(β) причём ф-ция ф(t) определена и непрерывна на отрезке α ≤t≤β то

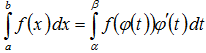
48. Интегрирование по частям в определенном интеграле.

ТЕОРЕМА. Пусть функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [а,b]. Тогда (4) где 

Формула (4) называется формулой интегрирования по частям для определенного интеграла.

49. Несобственные интегралы с бесконечными пределами (I рода).

Пусть   определена и непрерывна на множестве от   и  . Тогда:

Если  , то используется обозначение   и интеграл называетсянесобственным интегралом Римана первого рода. В этом случае   называется сходящимся.

Если не существует конечного   (  или  ), то интеграл   называется расходящимся к  , или просто расходящимся.

Пусть   определена и непрерывна на множестве от   и  . Тогда:

Если  , то используется обозначение   и интеграл называется несобственным интегралом Римана первого рода. В этом случае   называется сходящимся.

Если не существует конечного   (  или  ), то интеграл   называется расходящимся к  , или просто расходящимся.

Если функция   определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой: , где с — произвольное число.