19. Функции 2-х и 3-х переменных: способы задания, область определения и графики.

Определение. Если каждой паре (x,y) значений двух независимых переменных из области  ставится определенное значение z, то говорят, что z есть функция двух переменных (x,y).

z=f(x,y)

Геометрическое изображение функции двух переменных - поверхность.

Частное и полное приращение функции.

Полное приращение функции

z=f(x+x, y+y)f(x,y)

Частное приращение функции

_x z=f(x+x)f(x,y)

_y z=f(x,y+y)f(x,y)

Вообще, полное приращение функции не равно сумме частных приращений.

Пример. z=xy.

_x z=(x+x)yxy=yx

_y z=x(y+y)xy=xy

z=(x+x)(y+y)xy=yx+xy+yx  _y z+_x z.

Непрерывность функции нескольких переменных

Предел функции.

Пусть z=f(x,y) определена в некоторой окрестности A(x₀,y₀).

Определение. Постоянное число b называют пределом z=f(x,y) при P(x,y) стремящемся к A, если для любого  > 0 можно указать такое значение  > 0, что для всех x, удовлетворяющих неравенству AP < , имеет место неравенство f(x,y)b < .

Непрерывная функция

Частные производные

20. Частные производные 1-го порядка функции 2-х переменных. Их геометрический смысл.

Будем рассматривать функции трех независимых переменных. Пусть в некоторой трехмерной области Vзадана функция u=f(x,y,z) переменных x,y,z и пусть M₀(x₀,y₀,z₀) - некоторая внутренняя точка V. Дадим независимому переменному x приращение Δx=x-x₀, тогда функция и получит так называемое частное приращение по x:

Определение 1.7 Если существует конечный предел отношения частного приращения по X функции f(X,y,z) в точке m0(x0,y0,z0) к вызвавшему его

приращению Δx при Δx 0, то этот предел называется частной производной по х функции u=f(x,y,z) в точке М₀ и обозначается одним из символов:

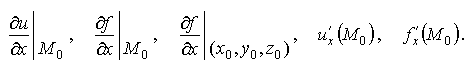
По определению,

Частные производные по y и по z определяются аналогично:

Производные f'_x, f'_y, f'_z называются ещё и частными производными первого порядка функции f(x,y,z), или первыми частными производными. Так как частное приращение Δxf(M₀) получается лишь за счет приращения независимой переменной x при фиксированных значениях других независимых переменных, то частная производная f'_x(M₀) может рассматриваться как производная функции f(x,y₀,z₀) одного переменного x. Следовательно, чтобы найти производную по x, нужно все остальные независимые переменные считать постоянными и вычислять производную по x как от функции одного независимого переменного x.

Аналогично вычисляются частные производные по другим независимым переменным.

Если частные производные существуют в каждой точке области V, то они будут функциями тех же независимых переменных, что и сама функция.

Геометрический смысл частных производных функции двух переменных

Графиком функции z= ƒ (х; у) является некоторая поверхность .График функции z = ƒ (х; у₀) есть линия пересечения этой поверхности с плоскостью у = у_о. Исходя из геометрического смысла производной для функции одной переменной ,заключаем, что ƒ'x(х_о;у_о) = tg а, где а — угол между осью Ох и касательной, проведенной к кривой z = ƒ (х; у₀) в точке Мо(хо;уо; ƒ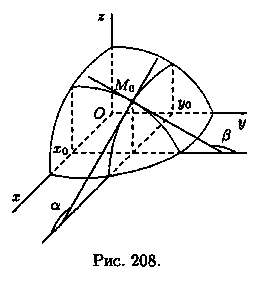 (хо;уо))

Аналогично, f'y (х₀;у₀)=tgβ.

21. Частные производные высших порядков ФНП.

Ч астные производные называют частными производными первого порядка. Их можно рассматривать как функции от (х;у) є D. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:

Аналогично определяются частные производные 3-го, 4-го и т. д. порядков.

Так, и т.д.Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Таковыми являются, например,

22. Частные дифференциалы (1-го порядка) ФНП.

Введем понятие дифференциала высшего порядка. Полный дифференциал функции (формула (44.5)) называют также дифференциалом первого порядка.

Пусть функция z=ƒ(х;у) имеет непрерывные частные производные второго порядка. Дифференциал второго порядка определяется по формуле (d²z = d(dz). Найдем его:

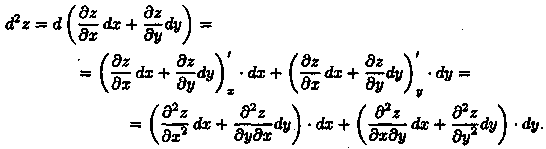
Отсюда: Символически это записывается так:

Аналогично можно получить формулу для дифференциала третьего порядка: где Методом математической индукции можно показать,что Отметим, что полученные формулы справедливы лишь в случае, когда переменные х и у функции z = ƒ(х;у) являются независимыми.

23. Полное приращение ФНП и ее дифференцируемость.

Полным приращением функции двух переменных z = f (x, y) в точке (x, y), вызванным приращениями аргументов  и , называется выражение .

Функция z = f (x, y) называется непрерывной в точке (x, y), если бесконечно малым приращениям аргументов соответствует бесконечно малое полное приращение функции.

Если обозначить  – расстояние между близкими точками  и (х, у), то  – это определение непрерывности ФНП на языке приращений.

Если функция z = f (x, y) непрерывна в любой точке (х, у)D, то она называется непрерывной ФНП в области D.

 Функция z = f (x, y), полное приращение z которой в данной точке (x, y) может быть представлено в виде суммы двух слагаемых: выражения, линейного относительно  и , и величины, бесконечно малой более высокого порядка малости относительно , называется дифференцируемой ФНП в данной точке, а линейная часть ее полного приращения называется полным дифференциалом ФНП.

Если , где  –бесконечно малые при , то полный дифференциал функции z = f (x, y) выражается формулой: , или:

  (1) Вычисление площади полной поверхности Тройной интеграл

(приращения независимых переменных совпадают с их дифференциалами: х = dx, y = dy).

Из определения полного дифференциала следует его связь с полным приращением: при малых  и  полное приращение функции z примерно равно ее полному дифференциалу:  с точностью до бесконечно малых более высокого порядка малости относительно .