
- •1. Радиоэл-ка как обл-ть науки и техники. Осн напр-я соврем радиоэ-ки;
- •4. Активные компоненты радиоэлектроники. Полупроводниковые электронные приборы. Интегральные микросхемы;
- •6. Собственная электропроводность полупроводниковых материалов.
- •7. Типы электрических переходов. Равновесное состояние p-n перехода. Контактная разность потенциалов.
- •8. Прямое смещение p-n перехода.
- •9. Вольтамперная характеристика (вах) p-n перехода. Основные свойства p-n перехода.
- •10Устройство и классификация полупроводниковых диодов. Система условных обозначений диодов;
- •11.Выпрямительные диоды и стабилитроныВыпрямительные диоды
- •12.Варикапы и диоды с барьером Шоттки
- •13.Импульсные диоды и диоды с накоплением заряда (днз) Импульсные диоды этот диод, имеющий малую длительность перех проц-в и предназн для работы в импульсных устройствах.
- •Параметры импульсных диодов
- •Диоды с накоплением заряда
- •14.Туннельные и обращенные диоды
- •15. Определение, устройство и классификация биполярных транзисторов. Система обозначений транзисторов;
- •19. Режимы работы и схемы включения биполярного транзистора
- •20. Принцип действия транзистора
- •Токи в транзисторе ток эмиттера имеет две составляющие: электронную и дырочную
- •21. Формальная модель биполярного транзистора. Система h-параметров биполярного транзистора
- •22. Статические вольтамперные характеристики биполярного транзистора. Влияние температуры на вах биполярного транзистора
- •23. Дифференциальные параметры биполярного транзистора. Определение h-параметров транзистора по статическим вах
- •Определение h–параметров по статическим характеристикам
- •24.Моделирование биполярного транзистора в режиме большого сигнала;
- •25.Малосигнальная модель биполярного транзистора;
- •26 Частотные свойства биполярного транзисторов
- •27 Физические параметры биполярного транзистора. Эквивалентные схемы замещения биполярного транзистора.
- •28.Основные параметры биполярного транзистора;
- •29. Классификация сигналов. Гармонический анализ сигналов
- •30. Спектральный анализ периодических сигналов. Комплексная форма ряда Фурье
- •31. Спектральный анализ непериодических сигналов
- •32. Амплитудно-модулированные сигналы
- •33. Частотно-модулированные сигналы
- •34. Фазомодулированные сигналы
- •35. Случайные сигналы
- •36. Моментные функции второго порядка;
- •37)Спектральный анализ случайных сигналов. Помехи
- •38. Характеристики линейных цепей. Комплексный коэффициент передачи;
- •39. Амплитудно-частотная характеристика.
- •40. Переходная характеристика;
- •41. Импульсная характеристика;
- •42. Методы исследования линейных электрических цепей;
- •43. Классификация аналоговых электронных устройств.
- •Классификация аналоговых электронных устройств
- •44. Основные параметры аналоговых электронных устройств;
- •45. Основные характеристики аналоговых электронных устройств;
- •46. Классификация усилительных устройств;
- •47. Понятие рабочей точки;
- •48. Способы задания рабочей точки;
- •49. Способы стабилизации рабочей точки;
- •50. Основные режимы работы усилительных каскадов;
- •51. Обратные связи в усилительных каскадах;
- •52. Усилительный каскад по схеме с общим эмиттером;
- •Эквивалентная схема усилительного каскада в диапазоне средних частот
- •53. Усилительный каскад по схеме с общей базой;
- •54. Усилительный каскакаскад по схеме с общим коллектором;
- •55.Усилительный каскад с ои
- •56.Усилительный каскад с общим стоком (истоковый повторитель)
- •57. Двухтактный усилительный каскад
- •58. Резонансный усилитель
- •59. Усилители постоянного тока (упт)
- •60.Дифференц усил каскад
- •61. Операционные усилители
- •62. Понятие автоколебат с-мы. Принцип возникновения колебаний.
- •63. Основные теории процессов в автогенераторе;(без линейной теории)
- •64. Основные схемы lc-генераторов;
- •65. Трехточечные схемы генераторов. Кварцевые генераторы;
- •67. Режимы работы автогенератора. Автоген-ры с автоматич смещением.
- •1 .10.1. Однокаскадная схема rc-генератора
- •1.10.2. Двухкаскадная схема -генератора rc
- •69. Модуляция электрических сигналов;
- •70. Амплитудные модуляторы;
- •71. Частотные модуляторы;
- •72. Фазовые модуляторы;
- •73. Детектирование электрических сигналов;
- •74. Амплитудные детекторы
- •Основные хар-ки и параметры амплитуд. Детектора(из инета).
- •75. Фазовые детекторы;
- •76. Частотные детекторы
- •77. Электронные ключевые схемы. Электронные ключи на биполярных транзисторах;
- •78. Способы повышения быстродействия ключей на биполярных транзисторах;
- •79. Электронные ключи на полевых транзисторах
- •80. Алгебра логики и ее основные законы(дописать)
- •81. Диодно-транзисторная логика (дтл);
- •82. Транзисторно-транзисторная логика (ттл);
- •83. Эмиттерно-связанная логика (эсл);
- •84. Интегральная инжекционная логика.
- •86. Основные параметры цифровых интегральных схем;
- •87. Система обозначений цифровых интегральных схем;
- •88. Триггеры.
- •Параметры триггеров
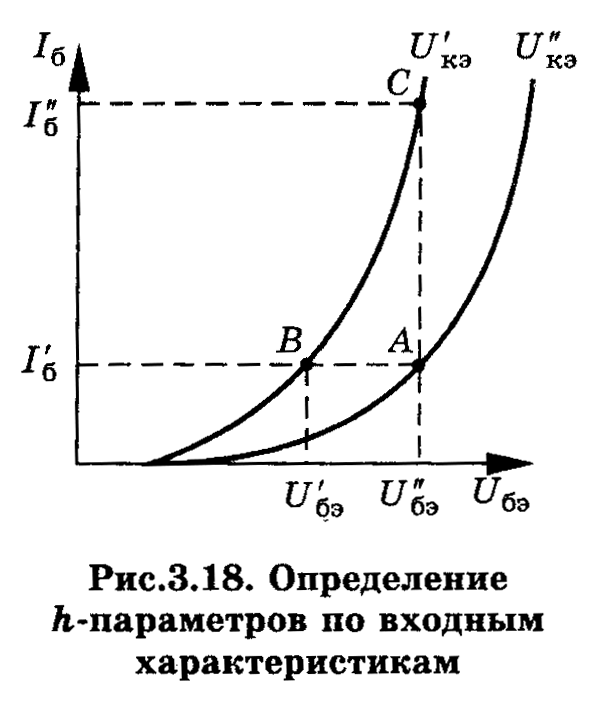
Определение h–параметров по статическим характеристикам
На низких частотах реактивные элементы транзистора практически не оказывают влияния на его работу, поэтому все параметры становятся вещественными величинами: Z–параметры переходят в r–параметры, Y–параметры в y–параметры и H– в h–параметры.
Приближенные значения h–параметров определяют графоаналитическим способом по входным и выходным статическим характеристикам. При определении h–параметров необходимо не менее двух характеристик каждого семейства. Параметры рассчитываются вблизи рабочей точки транзистора по линейным (конечным) приращениям токов и напряжений.
В результате таких замен уравнения в системе h–параметров имеют вид
![]() ;
;
![]() .
.
Параметры
![]() и
и
![]() определяются по входным характеристикам
(рис. 3.18).
Для этого на семействе входных
характеристик (например, для схемы с
ОЭ) в рабочей точке А строят треугольник,
отложив прямые, параллельные осям
абсцисс и ординат, до пересечения со
второй характеристикой.
определяются по входным характеристикам
(рис. 3.18).
Для этого на семействе входных
характеристик (например, для схемы с
ОЭ) в рабочей точке А строят треугольник,
отложив прямые, параллельные осям
абсцисс и ординат, до пересечения со
второй характеристикой.
Из полученного характеристического треугольника АВС находим все величины необходимые для определения h11э и h12э
![]()
 ,
,
![]() .
.
Параметры
![]() и
и
![]() определяются по выходным характеристикам
(рис. 3.19). Проведя через точку А'
вертикальную прямую до пересечения с
соседней характеристикой получаем
точку B'.
Затем выбираем в окрестности точки A'
точку C',
лежащую на той же характеристике так,
чтобы в пределах отрезка A'C'
характеристика была линейна. Тогда
определяются по выходным характеристикам
(рис. 3.19). Проведя через точку А'
вертикальную прямую до пересечения с
соседней характеристикой получаем
точку B'.
Затем выбираем в окрестности точки A'
точку C',
лежащую на той же характеристике так,
чтобы в пределах отрезка A'C'
характеристика была линейна. Тогда
![]() ;
;
![]() .
.
24.Моделирование биполярного транзистора в режиме большого сигнала;
При анализе работы транзистора в режиме большого сигнала, когда сильно проявляются нелинейные свойства, применяют эквивалентную схему, предложенную Эберсом и Моллом в 1954 году. Задача моделирования состоит в определении связи между статическими характеристиками и физическими параметрами транзистора.
П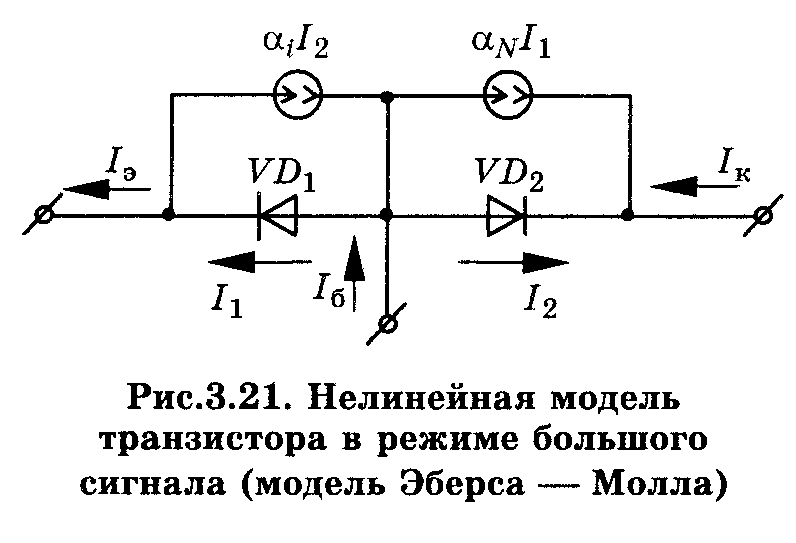 ростейший
вариант модели Эберса–Молла для n–p–n
транзистора показан на рис. 3.21 и
основан на интерпретации работы
транзистора, как прибора, имеющего два
взаимодействующих p–n
перехода.
ростейший
вариант модели Эберса–Молла для n–p–n
транзистора показан на рис. 3.21 и
основан на интерпретации работы
транзистора, как прибора, имеющего два
взаимодействующих p–n
перехода.
Диод
![]() моделирует свойства эмиттерного
перехода, а диод
моделирует свойства эмиттерного
перехода, а диод
![]() –
коллекторного. Источники тока
–
коллекторного. Источники тока
![]() и
и
![]() характеризуют соответственно передачу
тока эмиттерного перехода в коллектор
при нормальном включении и тока
коллекторного перехода в эмиттер при
инверсном включении транзистора.
характеризуют соответственно передачу
тока эмиттерного перехода в коллектор
при нормальном включении и тока
коллекторного перехода в эмиттер при
инверсном включении транзистора.
Таким образом, токи эмиттера и коллектора связаны с внутренними токами соотношениями
![]() ;
;
![]() . (3.18)
. (3.18)
Эмиттерный и коллекторный p–n переходы транзистора аналогичны p–n переходу диода. Если к одному из p–n переходов приложить напряжение, а выводы другого p–n перехода замкнуть между собой накоротко, то ток, протекающий через данный p–n переход, увеличится из–за изменения распределения носителей заряда в базе. Тогда токи через переходы запишутся так:
![]() ;
;
![]() , (3.19)
, (3.19)
где ![]() –
тепловой ток эмиттерного перехода,
измеренный при замкнутых накоротко
выводах базы и коллектора;
–
тепловой ток эмиттерного перехода,
измеренный при замкнутых накоротко
выводах базы и коллектора;
![]() –
тепловой ток коллекторного перехода,
измеренный при замкнутых накоротко
выводах базы и эмиттера
–
тепловой ток коллекторного перехода,
измеренный при замкнутых накоротко
выводах базы и эмиттера
Необходимо
помнить, что
![]() ,
–
это тепловые токи, а не обратные токи
переходов.
,
–
это тепловые токи, а не обратные токи
переходов.
Положительными
считаются токи
![]() ,
,
![]() и напряжения
и напряжения
![]() ,
,
![]() ,
соответствующие прямым включениям
переходов.
,
соответствующие прямым включениям
переходов.
В
простейшей модели диоды
![]() и
и
![]() отображают инжекцию (экстракцию)
носителей через эмиттерный и коллекторный
переходы. Связь между тепловыми токами
p–n переходов
отображают инжекцию (экстракцию)
носителей через эмиттерный и коллекторный
переходы. Связь между тепловыми токами
p–n переходов
![]() ,
,
включенными раздельно, и тепловыми
токами
и
получим из (3.18) и (3.19).
,
,
включенными раздельно, и тепловыми
токами
и
получим из (3.18) и (3.19).
Допустим,
что
![]() ,
,
![]() и при
и при
![]()
![]() получим
получим
![]() ;
;
![]() . (3.20)
. (3.20)
Тогда
токи
![]() и
и
![]() запишутся в следующем виде
запишутся в следующем виде
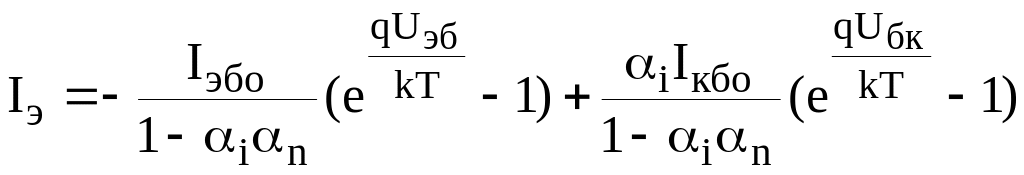 ; (3.21)
; (3.21)
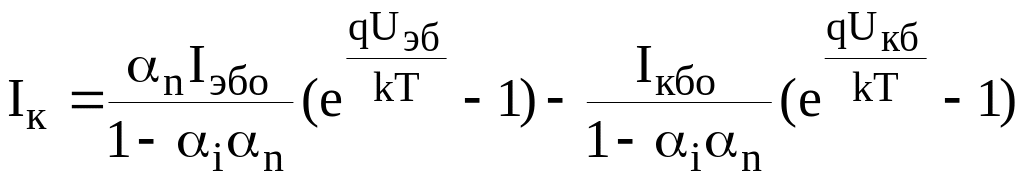 . (3.22)
. (3.22)
Полученные уравнения (3.21), (3.22) непосредственно определяют эмиттерный и коллекторный токи транзистора в соответствии с первым законом Кирхгофа (сумма всех токов в электрическом узле равна нулю), они также определяют и базовый ток прибора
![]() . (3.23)
. (3.23)
Из
выражений (3.21–3.23) можно получить
аналитические описание для любого
семейства характеристик при любой
схеме включения. Уравнение (3.21) определяет
семейство входных статических
характеристик для схемы с ОБ. Решив
уравнение (3.22) относительно
![]() и учитывая, что в транзисторе в общем
случае справедливо равенство
и учитывая, что в транзисторе в общем
случае справедливо равенство
![]() ,
,
получим выражение
![]() , (3.24)
, (3.24)
которое описывает выходные характеристики транзистора.
Решив
уравнение (3.21) относительно
![]() ,
получим выражение для идеализированных
входных (эмиттерных) характеристик
транзистора
,
получим выражение для идеализированных
входных (эмиттерных) характеристик
транзистора
![]() при
при
![]() = const
= const
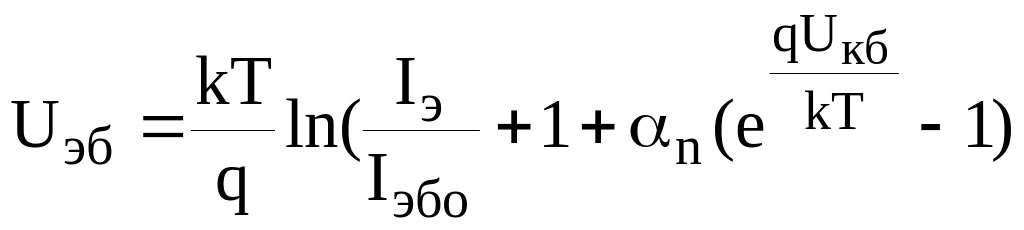 . (3.25)
. (3.25)
Модель Эберса–Молла описывает поведение транзистора в различных режимах работы, что может быть учтено выбором соответствующей полярности напряжений на эмиттерном и коллекторном переходах.
