
- •Пп 7. Аналитическая геометрия на плоскости
- •7.1. Прямая на плоскости. Основные определения и формулы
- •Простейшие задачи на плоскости Расстояние между двумя точками
- •Деление отрезка в данном отношении
- •Прямая линия на плоскости Общее уравнение прямой
- •Канонические и параметрические уравнения прямой
- •Уравнение прямой, проходящей через две точки
- •Уравнение прямой, проходящей через данную точку в заданном направлении
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
Простейшие задачи на плоскости Расстояние между двумя точками
M 1(x1,y1),
M2(x2,y2)
1(x1,y1),
M2(x2,y2)
![]()
![]() .
.
Деление отрезка в данном отношении
Т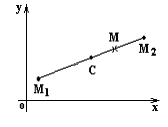 очка
M(x,y)
делит отрезок M1M2
в отношении
очка
M(x,y)
делит отрезок M1M2
в отношении
![]() ,
если
,
если
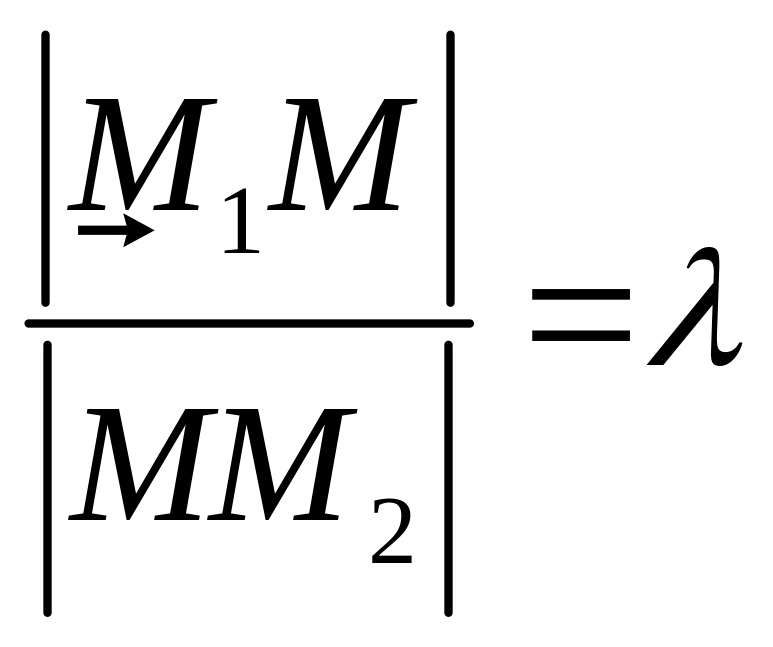 .
Тогда
.
Тогда
![]() а отсюда
а отсюда
 и координаты точки М
находятся по формулам:
и координаты точки М
находятся по формулам:
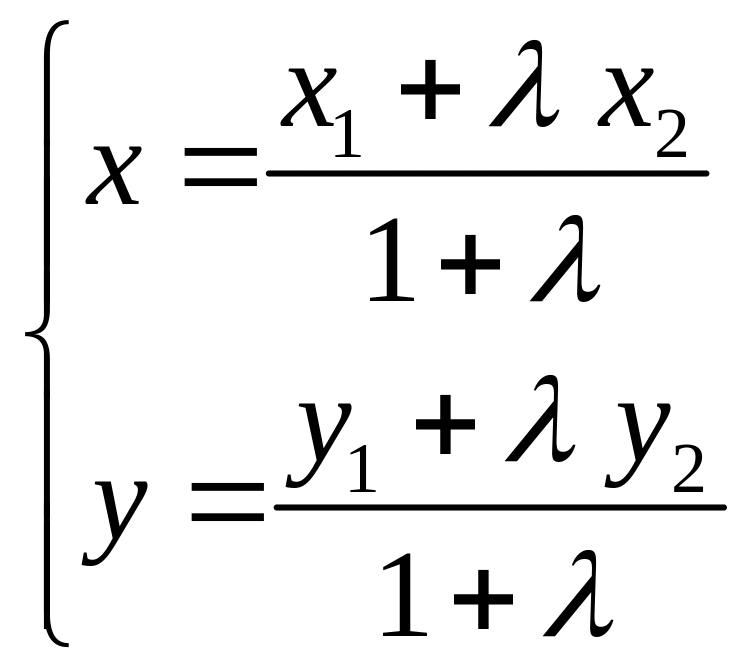 .
.
Координаты середины
отрезка С
получаются при М1М=ММ2,
то есть
![]() :
:
![]()
Отметим, что число не зависит от того, как выбрано положительное направление на отрезке М1М2, так как при изменении направления на противоположное не меняется.
Прямая линия на плоскости Общее уравнение прямой
Общее уравнение прямой на плоскости xoy получается из общего уравнения плоскости в пространстве при z = 0.
Прямая на плоскости в декартовых координатах задается уравнением
Ax+By+C=0.
Если А
= 0 (В
= 0), то прямая
параллельна оси ox
(оси oy).
Если С=0,
то прямая проходит через начало координат.
Если прямая проходит через точку (x0,y0)
перпендикулярно вектору
![]() ,
ее уравнение принимает вид:
,
ее уравнение принимает вид:
![]() .
.
Канонические и параметрические уравнения прямой
Если прямая проходит
через точку (x0,y0)
параллельно направляющему вектору
![]() ,
то из канонических и параметрических
уравнений прямой в пространстве при z
= 0 получаем каноническое и параметрические
уравнения прямой на плоскости в виде
,
то из канонических и параметрических
уравнений прямой в пространстве при z
= 0 получаем каноническое и параметрические
уравнения прямой на плоскости в виде
![]() и
и
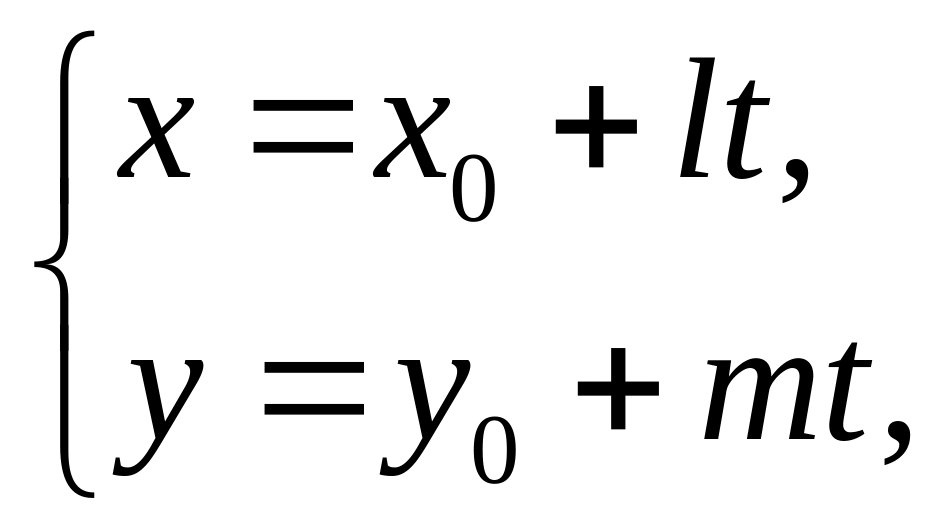
где t
– параметр,
![]() .
.
Уравнение прямой, проходящей через две точки
П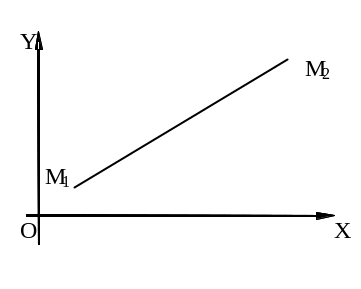 усть
на плоскости заданы две точки M1(x1,y1),
M2(x2,y2).
Для того чтобы написать уравнение
прямой, проходящей через эти точки,
полагаем в соответствующем уравнении
прямой в пространстве
усть
на плоскости заданы две точки M1(x1,y1),
M2(x2,y2).
Для того чтобы написать уравнение
прямой, проходящей через эти точки,
полагаем в соответствующем уравнении
прямой в пространстве
![]() Тогда получаем искомое уравнение в виде
Тогда получаем искомое уравнение в виде
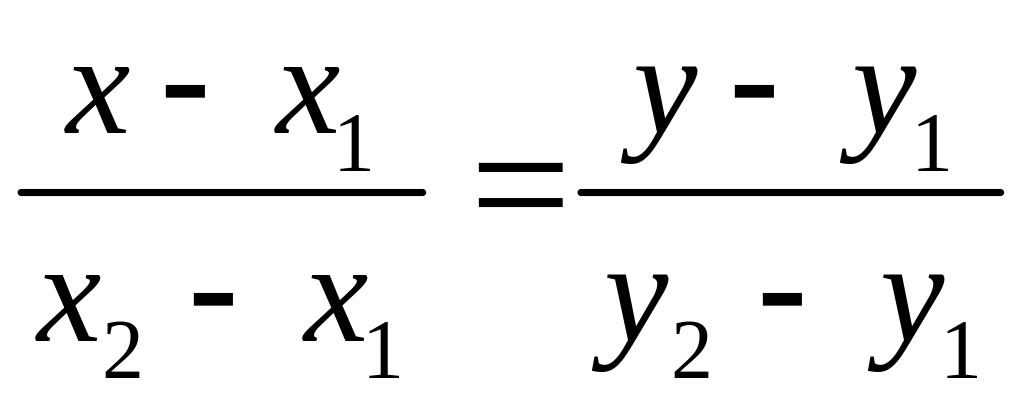 .
.
Уравнение прямой, проходящей через данную точку в заданном направлении
П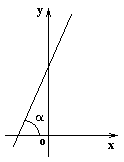 усть
прямая составляет угол
с осью OX.
Угловым коэффициентом прямой k
называется число
усть
прямая составляет угол
с осью OX.
Угловым коэффициентом прямой k
называется число
![]() .
.
Прямая может быть задана точкой М1(x1,y1) и угловым коэффициентом k или двумя точками М1(x1,y1) и М2(x2,y2).
Уравнение прямой
с угловым коэффициентом k
может быть получено из общего уравнения
прямой 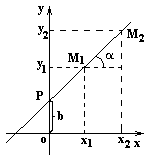 Ax+By+C=0,
если
Ax+By+C=0,
если
![]() ,
тогда
,
тогда
![]() ,
где
,
где
![]() и
и
![]() .
Прямая пересекает ось oy
в точке P(0,b).
.
Прямая пересекает ось oy
в точке P(0,b).
Из уравнения прямой, проходящей через две точки, имеем
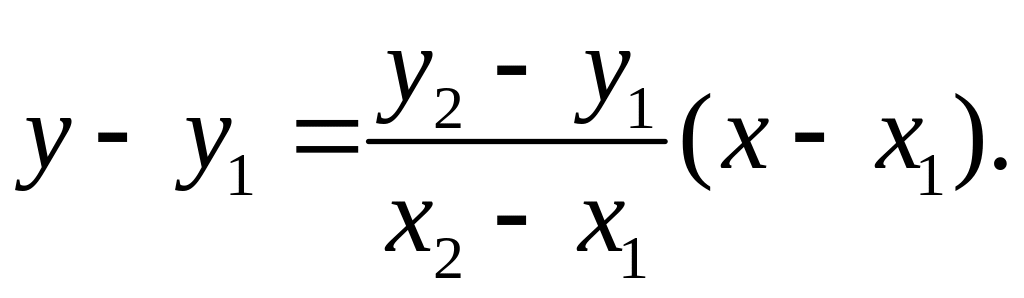
Отсюда
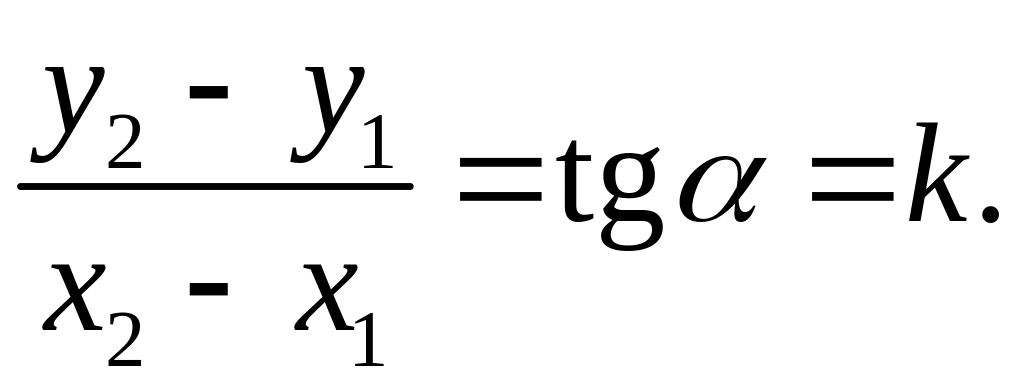 Таким образом,
Таким образом,
![]() Уравнение полученной прямой принимает
вид уравнения прямой с угловым
коэффициентом k,
если b =
y1
- k x1.
Уравнение полученной прямой принимает
вид уравнения прямой с угловым
коэффициентом k,
если b =
y1
- k x1.
Уравнение прямой в отрезках
Общее уравнение
прямой Ax+By+C=0
может быть преобразовано к виду уравнения
прямой «в отрезках»:
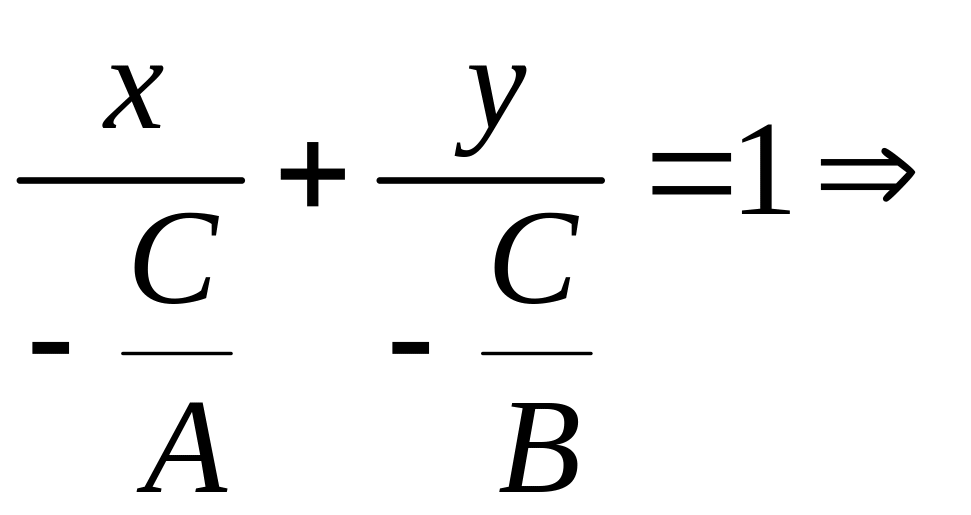
![]() .
Прямая пересекает ось ox
в точке А(а,0)
и ось oy
в точке В(0,b).
.
Прямая пересекает ось ox
в точке А(а,0)
и ось oy
в точке В(0,b).
Нормальное уравнение прямой
П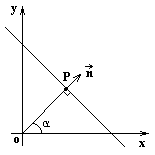 усть
известно расстояние от прямой до начала
координат
усть
известно расстояние от прямой до начала
координат
![]() и угол
между перпендикуляром к прямой и осью
ox.
Из нормального уравнения плоскости в
пространстве, полагая z
= 0 и учитывая,
что
и угол
между перпендикуляром к прямой и осью
ox.
Из нормального уравнения плоскости в
пространстве, полагая z
= 0 и учитывая,
что
![]() ,
,
получаем нормальное уравнение прямой на плоскости в виде:
![]() .
.
Нормальное уравнение
прямой можно получить из общего уравнения
прямой Ax+By+C=0,
умножив его на нормирующий множитель
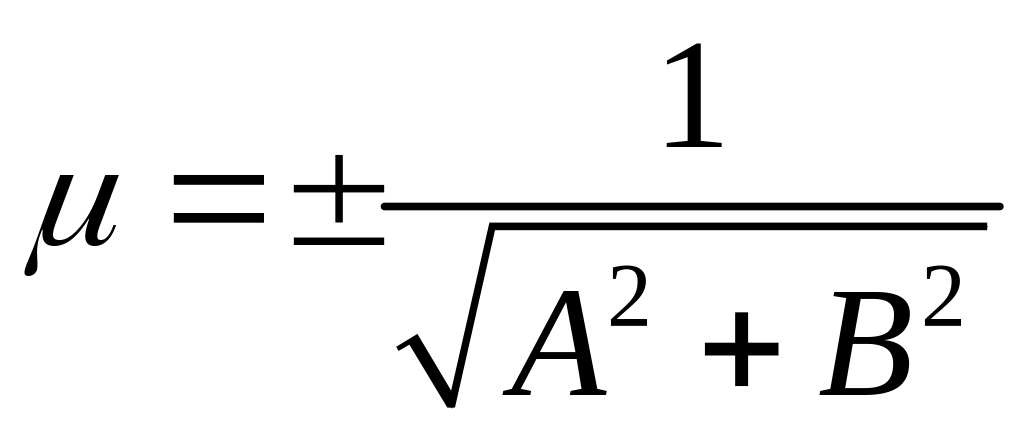 .
Знак числа
должен быть противоположен знаку числа
С.
.
Знак числа
должен быть противоположен знаку числа
С.
Косинусы углов, образуемых прямой с осями координат, называются направляющими косинусами прямой.
Если угол между
прямой и осью ox
равен
и угол между прямой и осью oy
равен ,
то
![]() .
.
Расстояние от точки до прямой
Расстояние d от точки M0(x0,y0) до прямой, задаваемой нормальным уравнением, равно модулю отклонения точки от прямой , d = ||,
где  .
.
По этой формуле положительно, если точка М0 и начало координат лежат по разные стороны от прямой, в противном случае отрицательно.
Координаты точки пересечения двух прямых
Если прямые заданы уравнениями A1x+B1y+C1=0 и A2x+B2y+C2=0, то координаты точки их пересечения (x0, y0) получаются как решение системы уравнений:
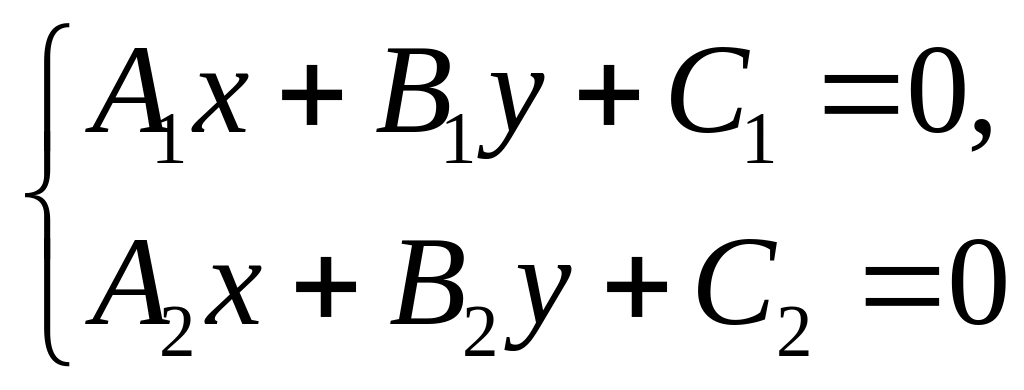
по формулам Крамера в виде:
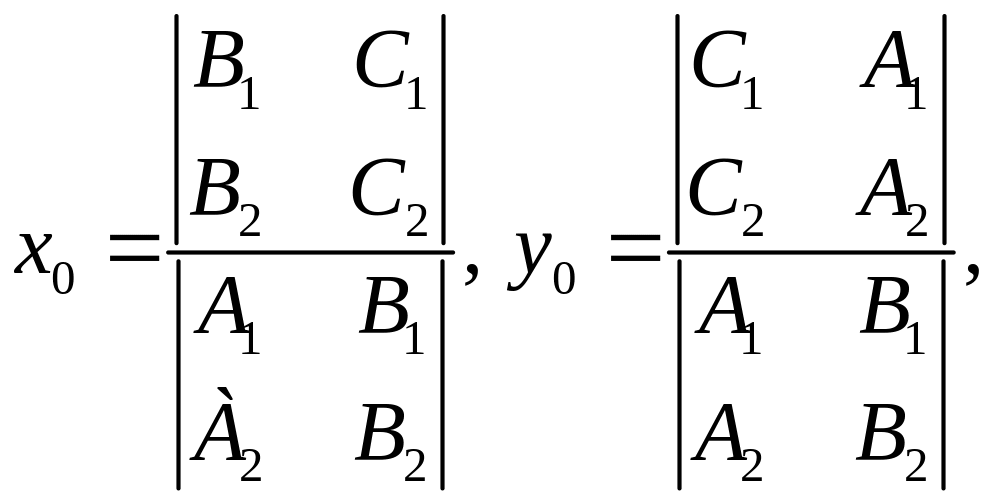 при
при
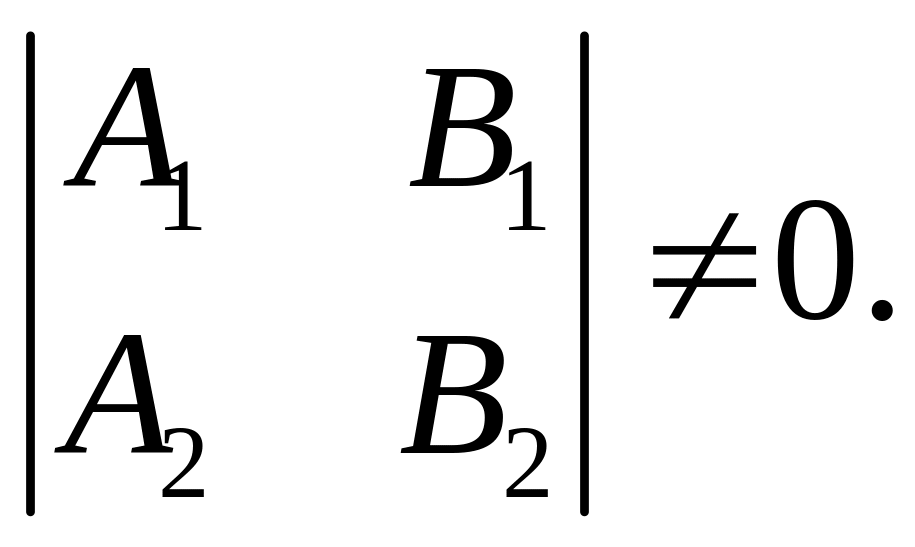
Угол между двумя прямыми
П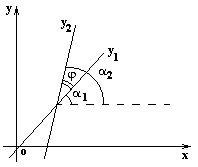 усть
две прямые заданы уравнениями:
усть
две прямые заданы уравнениями:
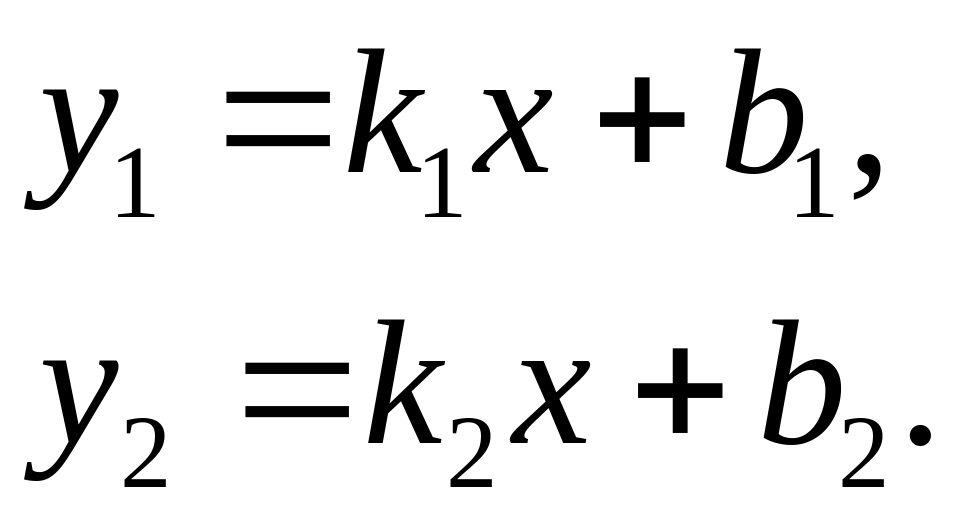
Острый угол пересечения этих прямых (отсчитываемый против часовой стрелки) находится из следующих соотношений:
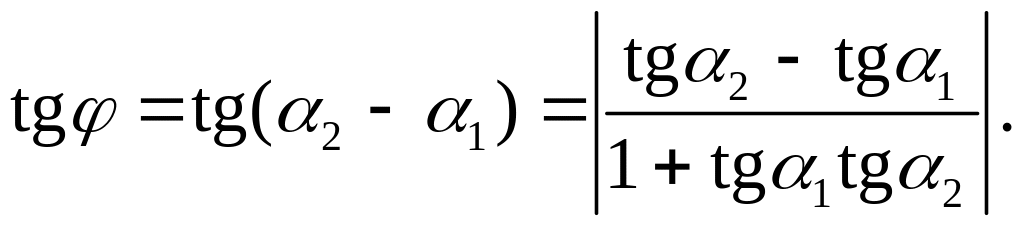
Отсюда
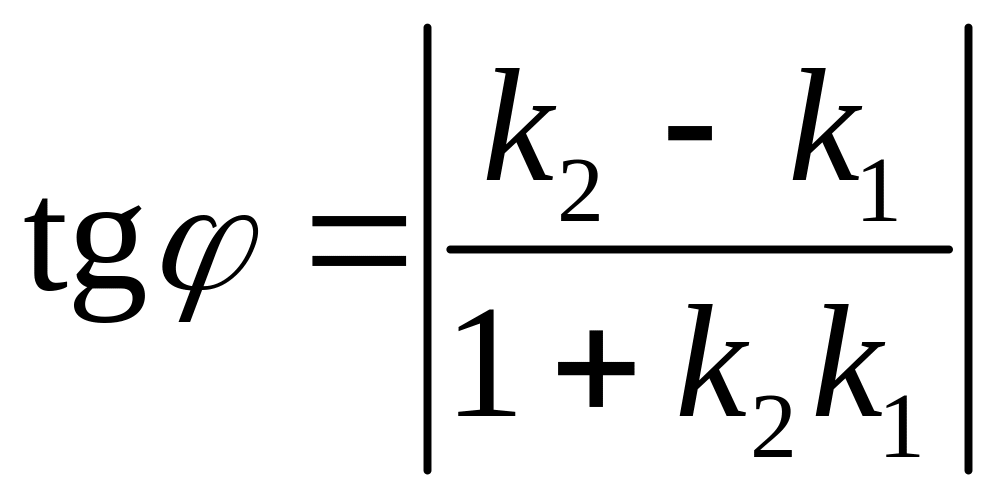 .
.
Если прямые заданы
общими уравнениями А1x+B1y+C1=0
и A2x+B2y+C2=0,
то угловые коэффициенты прямых равны:
 и угол
между прямыми определяется формулой:
и угол
между прямыми определяется формулой:
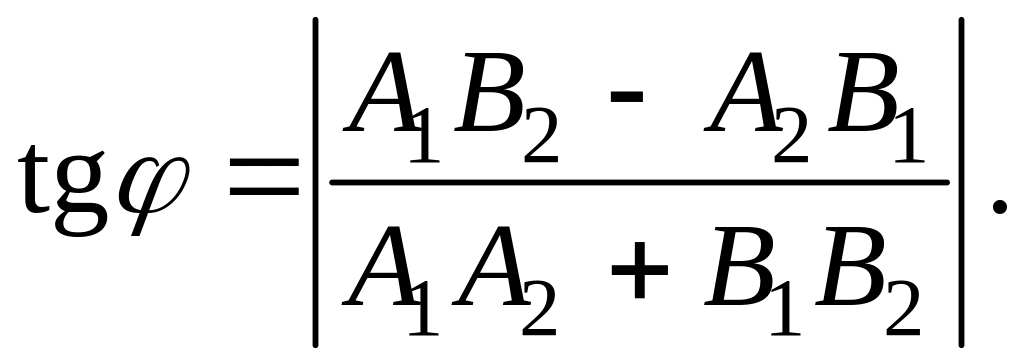
Условие параллельности и перпендикулярности двух прямых
Прямые y1=k1x+b1
и y2=k2x+b2
параллельны друг другу, если
![]() .
Следовательно,
.
Следовательно,
![]() ,
то есть k1=k2.
,
то есть k1=k2.
Прямые y1=k1x+b1
и y2=k2x+b2
перпендикулярны друг другу, если
![]() .
Следовательно,
.
Следовательно,
![]() ,
то есть k1k2
= -1. Отсюда
,
то есть k1k2
= -1. Отсюда
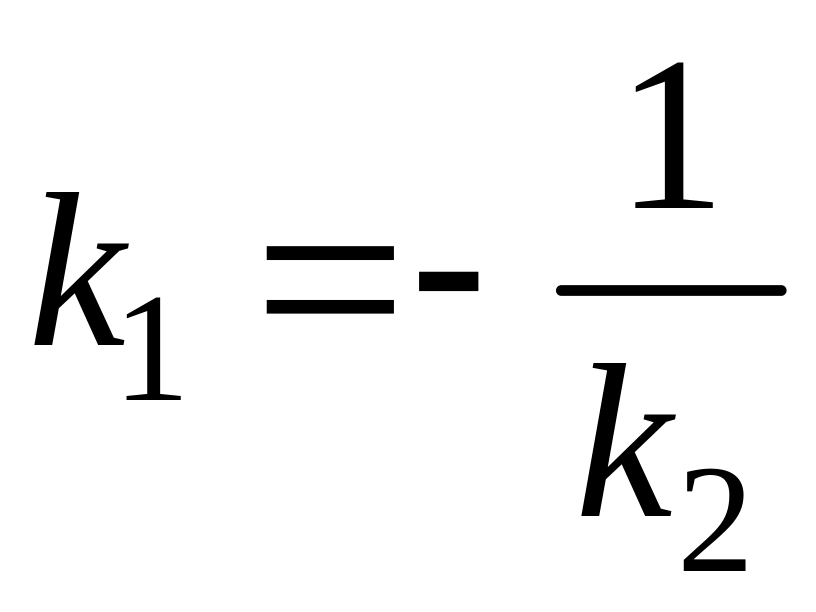 .
.
Если прямые заданы общими уравнениями, то:
А1В1
– А2В1=0,
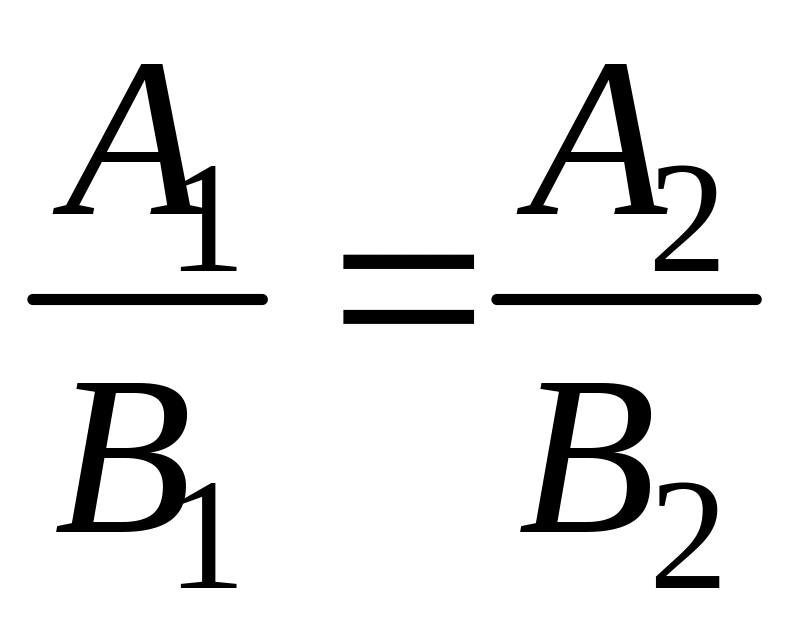 – условие параллельности,
– условие параллельности,
А1А2+В1В2=0 – условие перпендикулярности прямых.
Уравнение пучка прямых
Совокупность всех прямых плоскости, проходящих через некоторую точку M(x0,y0), называется пучком прямых с центром М0.
Если A1x+B1y+C1=0 и A2x+B2y+C2=0 - уравнения двух прямых, пересекающихся в точке М0; то уравнение A1x+B1y+C1+ (A2x+B2y+C2)=0
определяет все прямые пучка, кроме второй из прямых.
ПП 7.1. Прямая на плоскости
|
||
ПП 7.1. №1. |
треугольник задан уравнениями трех его сторон: АС: х – 2у + 5 = 0, АВ: х + 2у – 3 = 0, ВС: 2х + у – 15 = 0. Определите следующие элементы треугольника: а) координаты вершин, б) уравнения высот, в) уравнения медиан, г) длины сторон, д) уравнения биссектрис, ж) центр и радиус вписанной окружности, з) центр и радиус описанной окружности, и) центр тяжести треугольника, к) внутренние углы треугольника, л) площадь треугольника. Решение:
а) Координаты вершин треугольника находятся как точки пересечения соответствующих сторон. Так, например, координаты точки А являются решением системы уравнений
Аналогично находятся В (9, -3) и С (5, 5).
б) Высотой треугольника называется отрезок перпендикуляра, опущенного из вершины треугольника на противоположную сторону.
Так hc
= CC1
AB. Уравнение
высоты СС1
ищем как уравнение прямой у
= k1x
+ b, если
известен угловой коэффициент прямой
АВ:
Из условия перпендикулярности прямых k1 k2=-1 k1=2. Поскольку высота СС1 проходит через точку (5, 5), уравнение hc имеет вид: у – 5 = 2(х – 5) или у = 2х – 5.
Анализ уравнений
сторон АС:
в) Медианой называется отрезок прямой, соединяющей вершину треугольника с серединой противолежащей стороны. Координаты середин сторон находятся по формулам деления отрезка в данном отношении: С2 (4, -1/2), В2 (2, 7/2), А2 (7, 1). Уравнение медианы mC = CC2 получается как уравнение прямой, проходящей через точки С и С2:
Аналогично mВ: 13х+14у–75=0, mА: x+8y–15=0.
г) Длины сторон найдем по формуле расстояния между двумя точками:
д) Биссектрисой треугольника называется лежащий в треугольнике отрезок прямой, которая делит его внутренний угол пополам. Укажем два способа нахождения уравнения биссектрисы треугольника. 1). Биссектриса делит противолежащую сторону в отношении, пропорциональном прилежащим сторонам. Если С3 – точка пересечения биссектрисы lC = CC3 со стороной АС, то
Координаты точки С3 находим по формулам деления отрезка в данном отношении = 3/4: С3 (23/7, -1/7). Уравнение биссектрисы lC = CC3 получается как уравнение прямой, проходящей через точки С3 и С (5, 5):
2). Уравнение биссектрисы lC = CC3 может быть найдено из условия того, что точки биссектрисы CC3 равноудалены от сторон АС и СВ. Вычислим отклонения точки (х, у), лежащей на биссектрисе, от сторон АС и СВ (см. п.2.7):
АС
и СВ
отрицательны, так как начало координат
и точки биссектрисы треугольника
лежат по одну сторону от каждой из
сторон АС
и СВ.
Учитывая, что
d
= ,
уравнение биссектрисы получим из
равенства
или lC: 3х – у – 10 = 0. Для вычисления биссектрисы угла А lА применим второй способ.
Отклонение
Отклонение
Для биссектрисы lА справедливо -АС = АВ,
то есть
Следовательно, 4у = 8. Таким образом, lА: у = 2. уравнение lВ: х+у – 6 = 0 может быть найдено одним из двух способов.
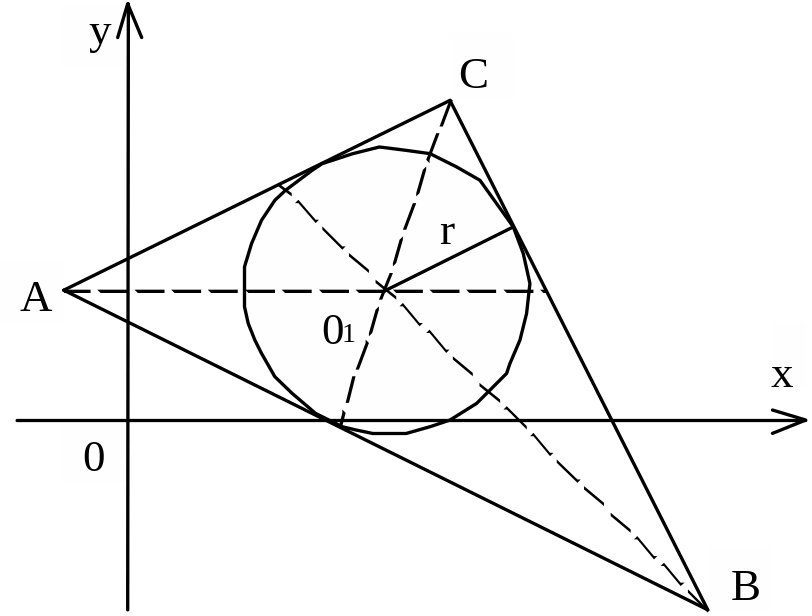
ж) Центр вписанной окружности находится в точке пересечения биссектрис lС и lА треугольника.
Система уравнений, составленная из уравнений биссектрис:
имеет решение х = 4, у = 2. Следовательно, центр вписанной окружности находится в точке О1 (4, 2).
Радиус вписанной
окружности найдем как расстояние от
точки О1
до стороны АС:
Таким образом,
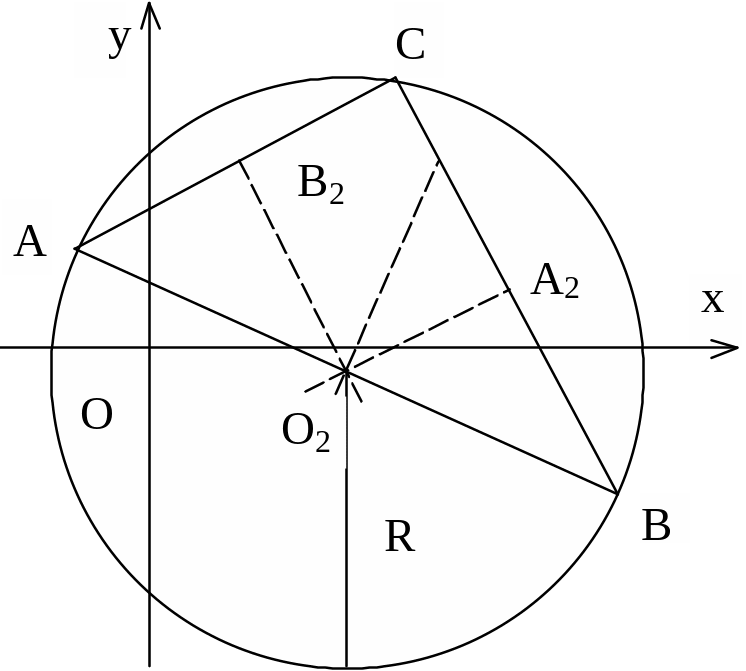
з) Центр описанной окружности находится в точке пересечения серединных перпендикуляров.
Координаты середин сторон АС и АВ найдены в п.в): С2 (4, -1/2), В2 (2, 7/2).
Уравнения линий
серединных перпендикуляров
Угловые коэффициенты равны 2 и -2 соответственно, и эти прямые проходят через точки С2 и В2, их уравнения имеют вид:
Система уравнений, составленная из уравнений серединных перпендикуляров:
имеет решение х = 4, у = -1/2. Следовательно, центр описанной окружности находится в точке О2 (4, -1/2).
Центр описанной
окружности прямоугольного треугольника
лежит на середине АВ:
и) Центр тяжести треугольника находится в точке пересечения медиан.
1)
Из п.в) имеем систему уравнений для
определения координат центра тяжести
как точки пересечения медиан mС
и mB
:
Система имеет решение х = 4,33, у = 1,3. Следовательно, центр тяжести треугольника находится в точке О3 (4,33; 1,3). 2) Укажем, что медианы треугольника делятся точкой пересечения в отношении 2 : 1, считая от вершины.
Таким
образом, координаты центра тяжести
могут быть найдены как координаты
точки О3,
делящей медиану в отношении
Если воспользоваться формулами деления отрезка в данном отношении, то координаты точки:
и)
Внутренние
углы
треугольника могут быть найдены через
угловые коэффициенты прилежащих
сторон. Например, внутренний угол при
вершине А
треугольника
Следовательно, А = arctg(4/3).
к) По формуле площади треугольника имеем
1)
2) Площадь треугольника может быть вычислена по формуле: S = p r, где p – полупериметр треугольника; r – радиус вписанной окружности.
Поскольку
(кв. ед.).
|
а) А (-1, 2), В (9, -3), С (5, 5), б)
у=-2х+15, у=2х–5, в) x+8y–15=0, 13х+14у–75=0, 11х–2у–45=0,
г)
д) у = 2, х+у–6=0, 3х–у–10=0, ж)
О1(4,2),
з)
О2(4,-1/2),
и)
к) 30.
|
ПП 7.1. №2. |
Найдите проекцию точки Р (4, 9) на прямую, проходящую через точки А (3, 1) и В (5, 2). Решение: Искомую
точку М
Уравнение
перпендикуляра из точки Р
на прямую АВ
ищем в виде
у
– 9 =
k (x
– 4); из
условия перпендикулярности
|
|
ПП 7.1. №3. |
Постройте прямую 3х – 5у + 15 = 0. Решение:
Уравнение прямой
в отрезках имеет вид:
|
5х + 12у+ + 6 = 0 |
ПП 7.1. №4. |
Даны две прямые 2х + 3у – 5 = 0, 7х +15у +1 = 0, пересекающиеся в точке М. Составьте уравнение прямой, которая проходит через точку М перпендикулярно к прямой 12х – 5у – 1 = 0. Решение: Прямые
2х + 3у – 5 + l×(7х + 15у +1) = 0, (2 + 7l)×х + (3 + 15l)×у + (-5 + l) = 0
Выделим в этом
пучке искомую прямую
5х + 12у + 6 = 0.
|
|
ПП 7.1. №5. |
Напишите уравнение прямой L, проходящей через точку М (2, 1) под углом 45 к прямой L1: 2х + 3у +4 = 0. Решение:
L1: 2х + 3у +4 =
0,
|
|
ПП 7.1. №6. |
Составьте уравнение прямой L, параллельной прямым L1: х + 2у – 1 = 0 и L2: х + 2у +2 = 0 и проходящей посередине между ними.
Решение:
1-ый способ.
Уравнение прямой L
будем искать в виде А(х
– х0)
+ В(у
+ у0)
= 0.
В качестве нормального вектора
{1, 2}. Найдем какую-нибудь точку М0 (х0, у0) L. Точка М0 будет делить пополам отрезок, соединяющий две любые точки, лежащие на L1 и L2. Например, М1 (1, 0) L1 и М2 (-2, 0) L2, тогда точка М0 имеет координаты (-1/2, 0), и уравнение прямой L принимает вид: х + 2у + 1/2 = 0. 2 –ой способ. Произвольная точка М (х, у) L, если (М, L1) = (М, L2) . Для снятия модуля определим знаки отклонений точки М (х, у) от прямых L1 и L2. Для этого нужно выяснить взаимное расположение начала координат, точки М (х, у) и прямых L1 и L2. Приведем уравнения прямых к нормальному виду:
где
Видим,
что
Из
х + 2у – 1 = -х – 2у – 2 и х + 2у + 1/2 = 0.
|
х+2у+1/2=0 |


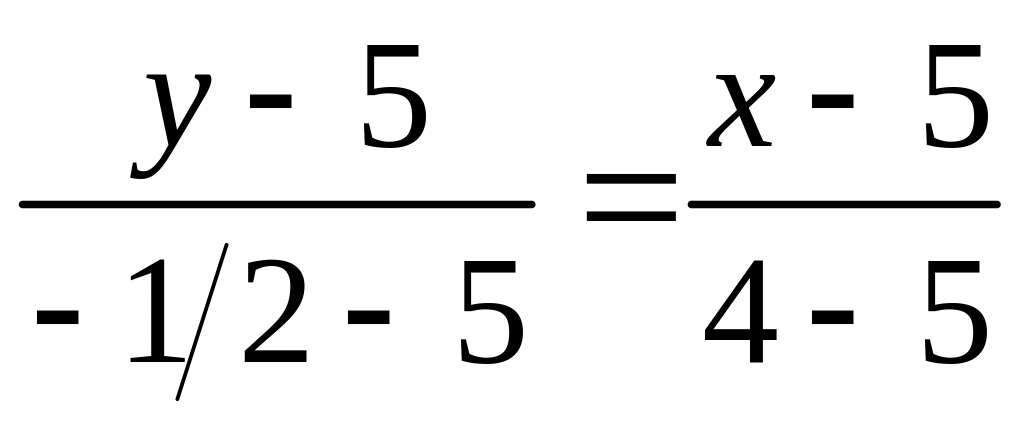 или mC:
11х–2у–45=0.
или mC:
11х–2у–45=0.
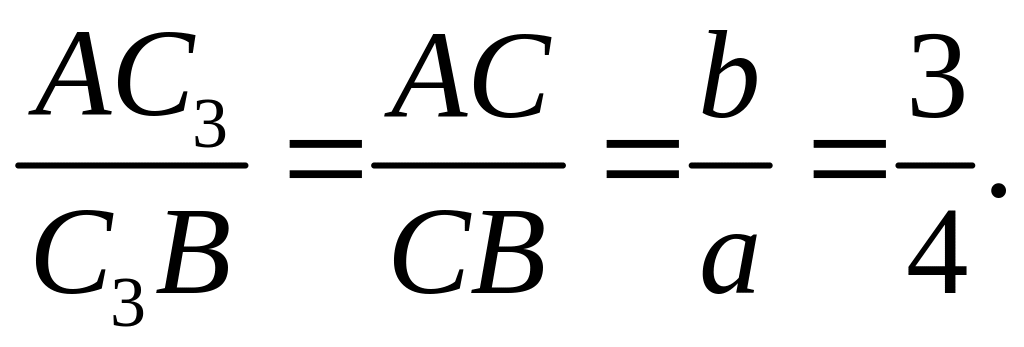
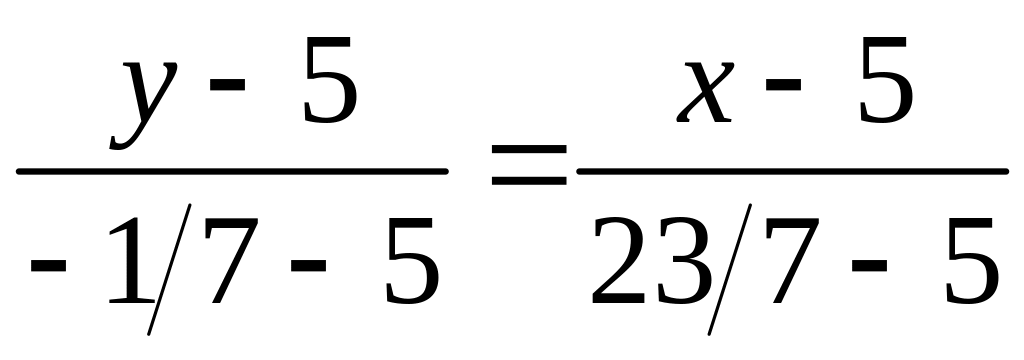 или 3х
– у – 10 =
0.
или 3х
– у – 10 =
0.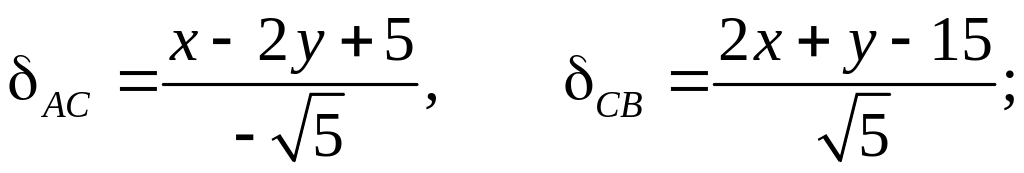
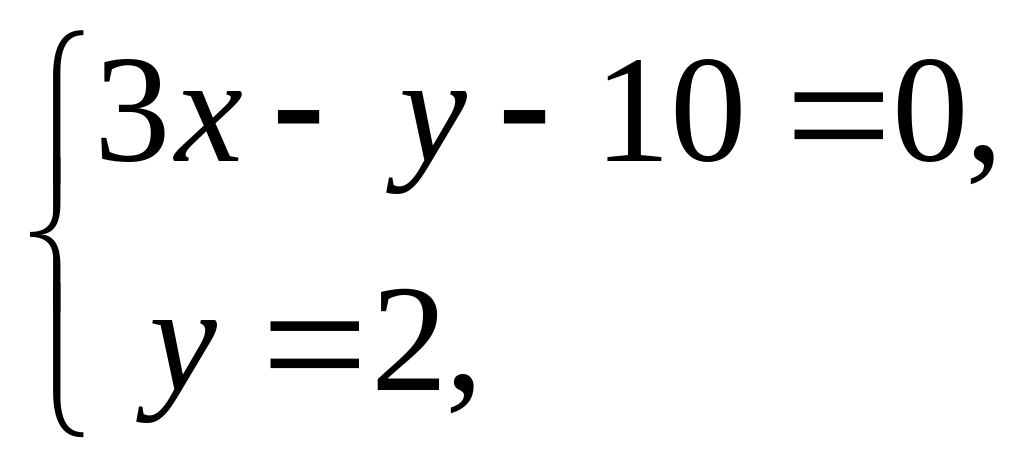
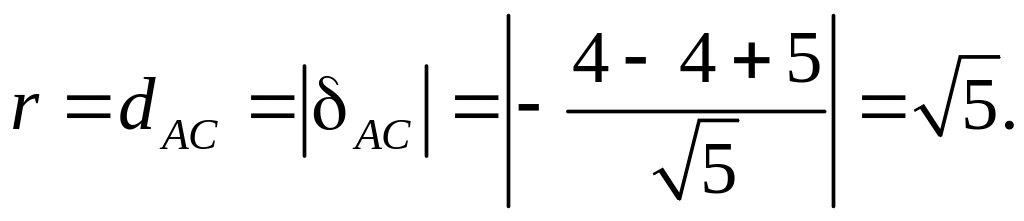

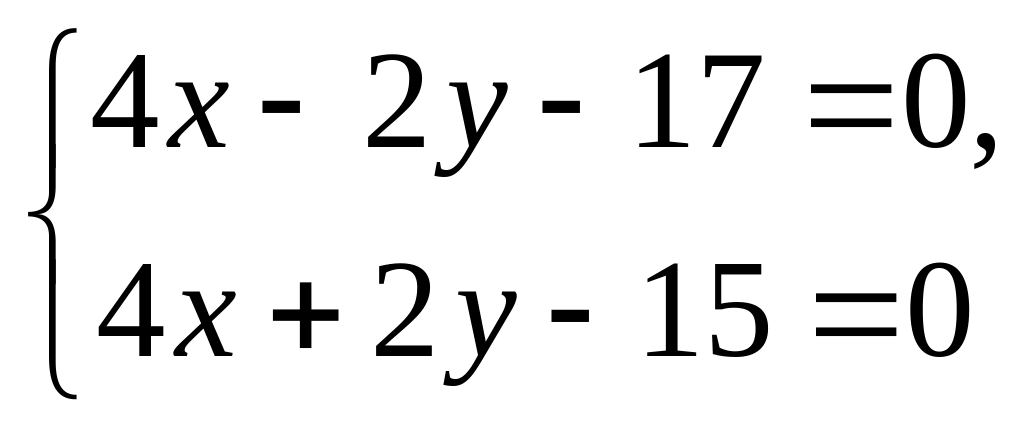 ,
,
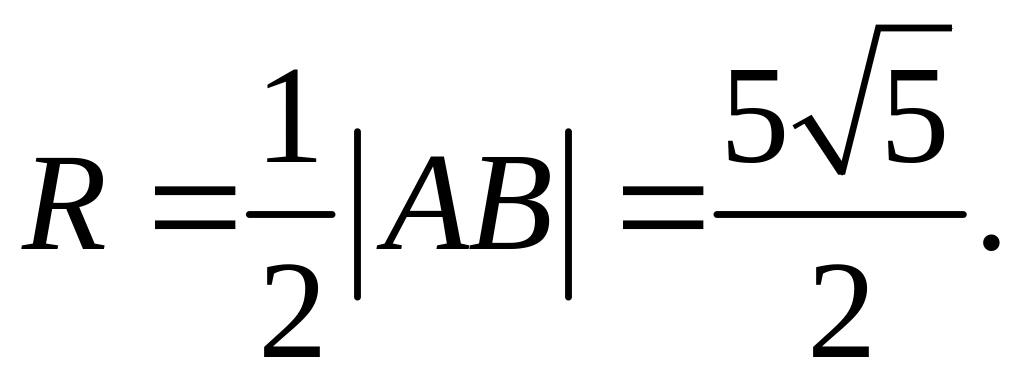
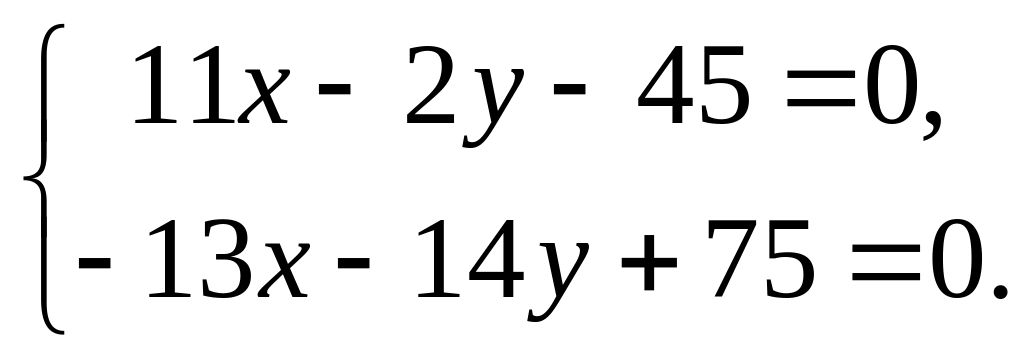
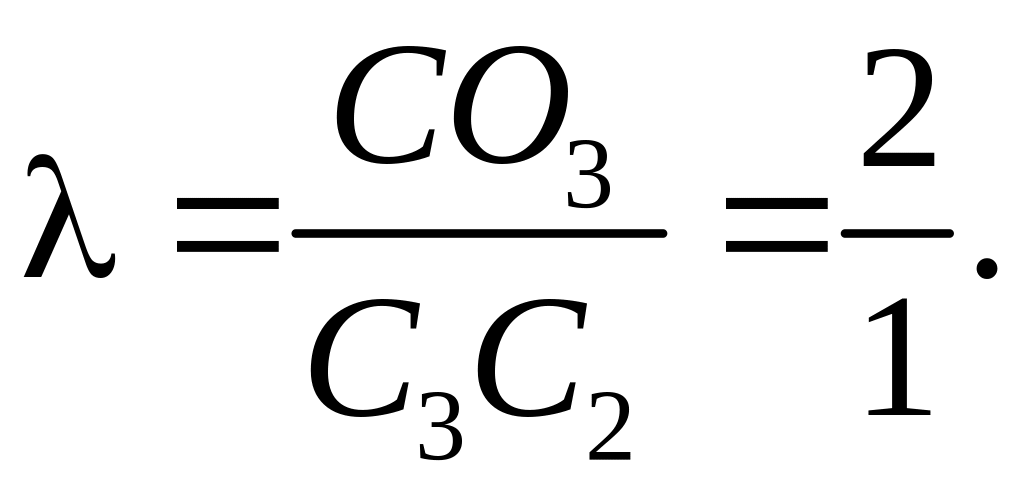

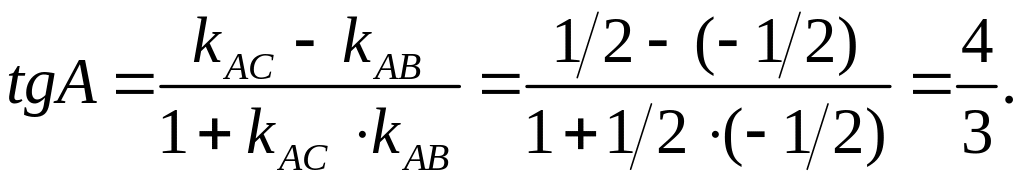
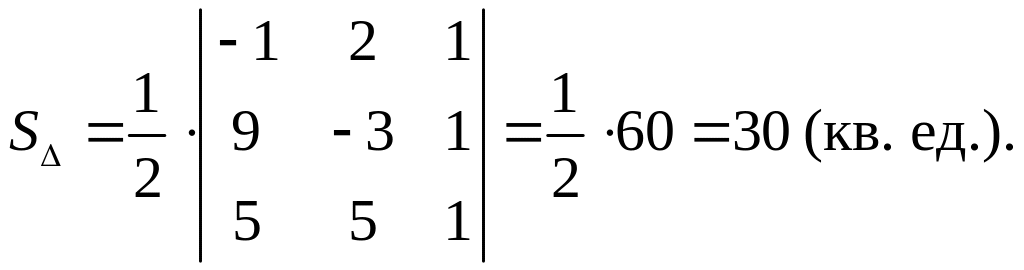
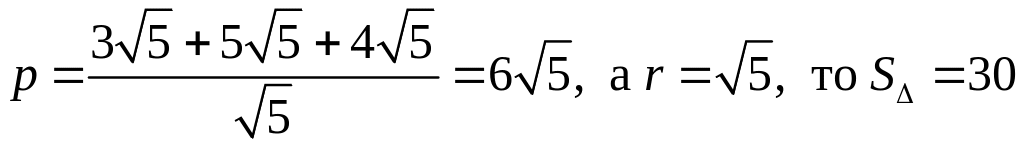
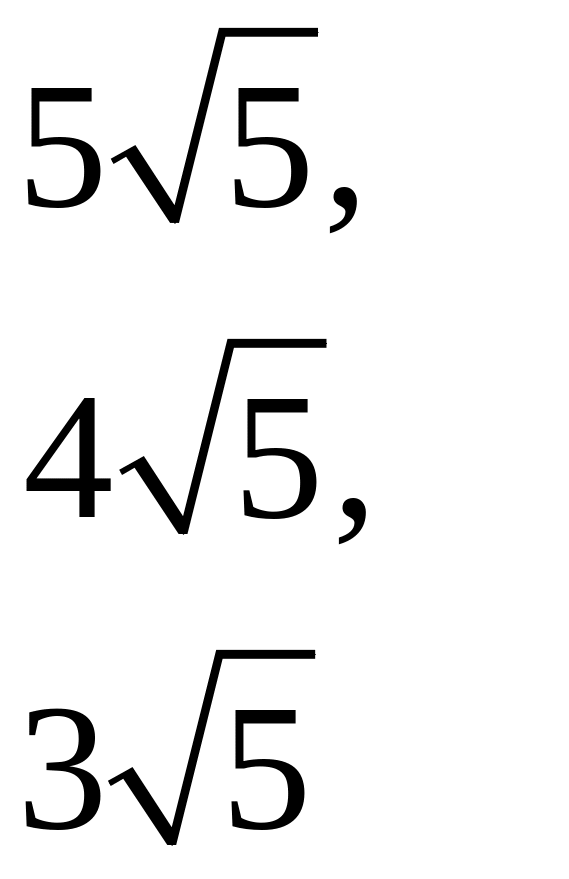 ,
, ,
, ,
,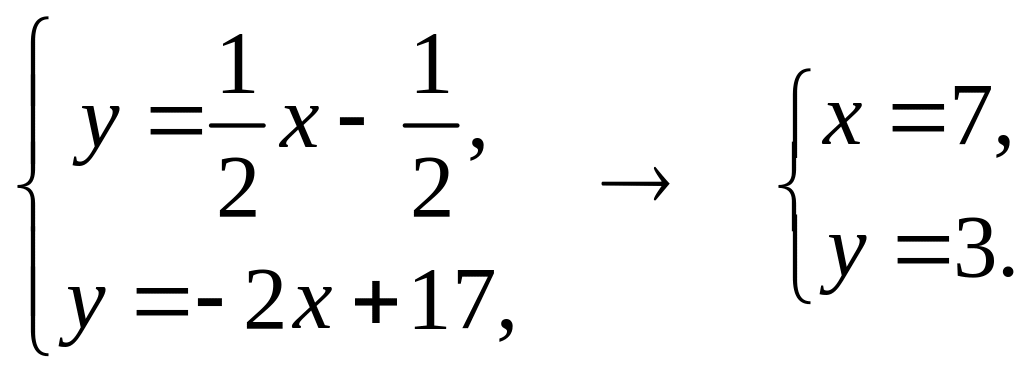 М
=
М
=
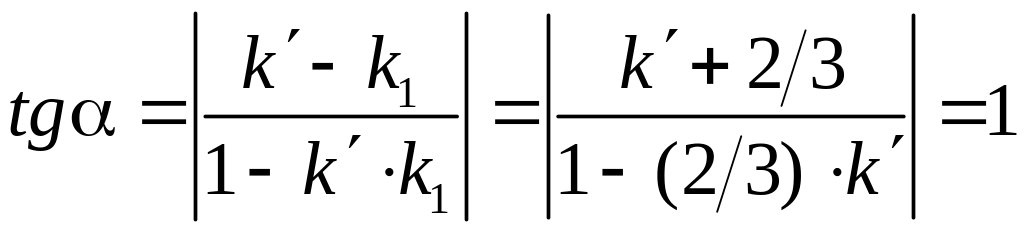
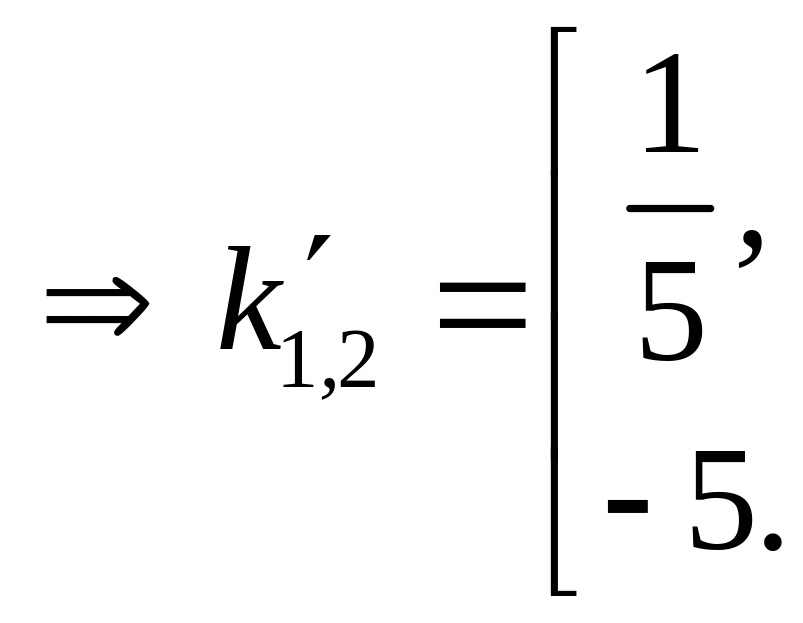 М (2,1)
М (2,1)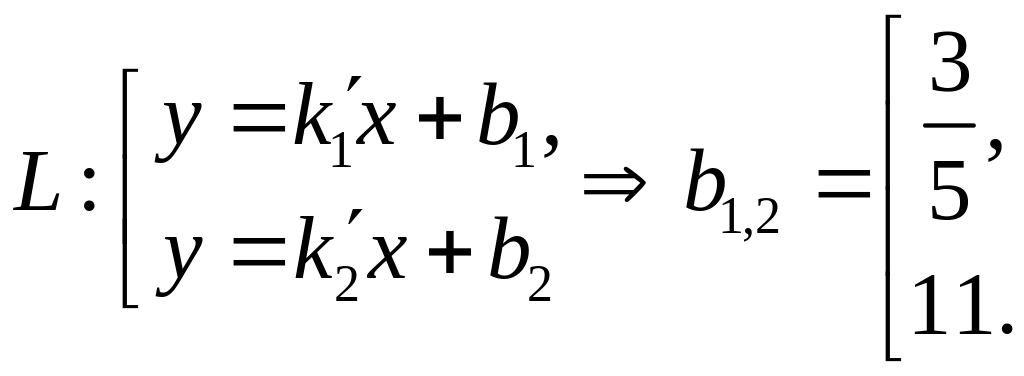

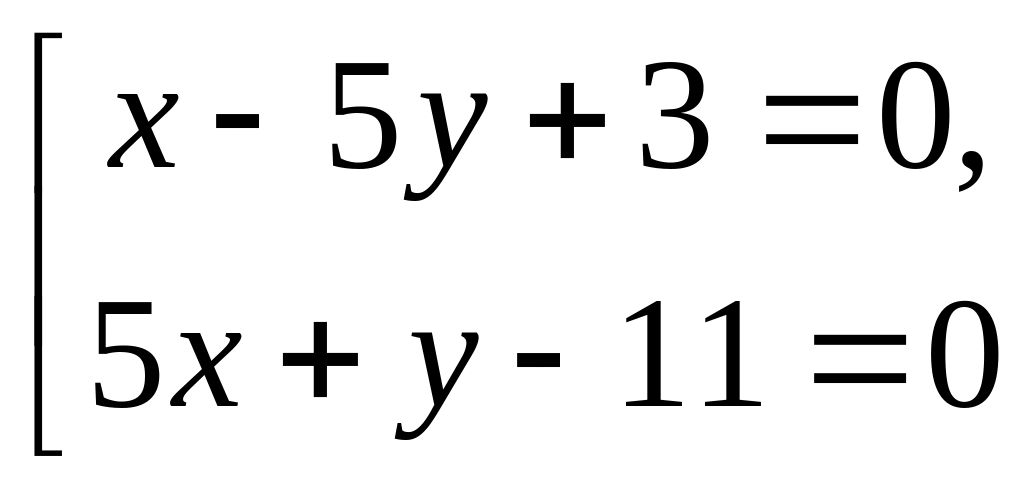


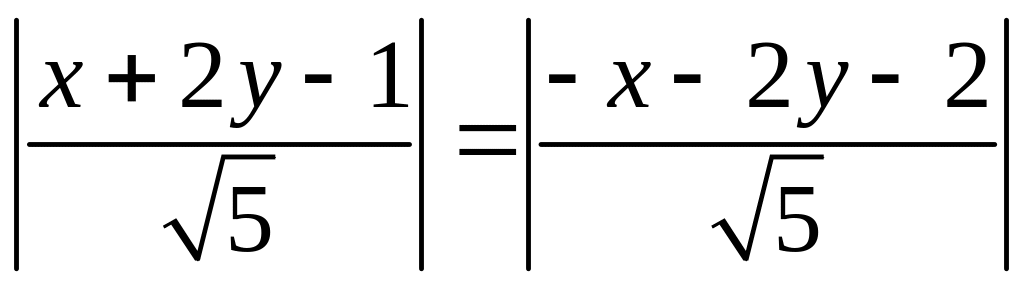 следует, что
следует, что