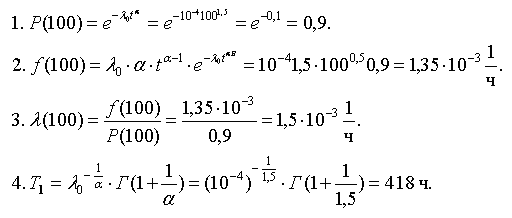5. Коэффициент технического использования

Коэффициент технического использования К_ТИ равен отношению математического ожидания суммарного времени пребывания объекта в работоспособном состоянии за некоторый период эксплуатации к математическому ожиданию суммарного времени пребывания объекта в работоспособном состоянии и простоев, обусловленных техническим обслуживанием и ремонтом за тот же период эксплуатации:

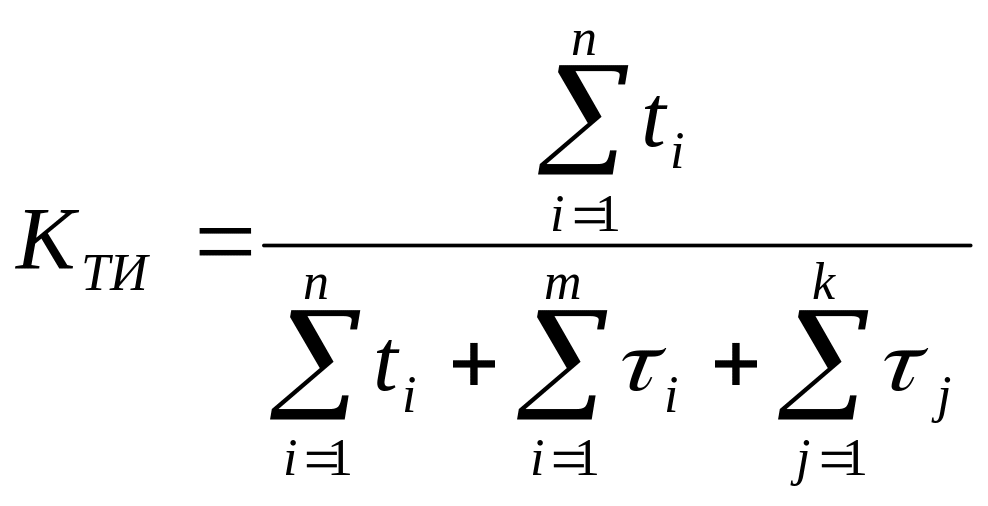(31)

где t_i - время сохранения работоспособности в i-м цикле функционирования объекта; _I - время восстановления (ремонта) после i-го отказа объекта; _j - длительность выполнения j-й профилактики, требующей вывода объекта из работающего состояния (использования по назначению); n - число рабочих циклов за рассматриваемый период эксплуатации; m - число отказов (восстановлений) за рассматриваемый период; k - число профилактик, требующих отключения объекта в рассматриваемый период.

Как видно из выражения (31), коэффициент технического использования характеризует долю времени нахождения объекта в работоспособном состоянии относительно общей (календарной) продолжительности эксплуатации. Следовательно, К_ТИ отличается от К_Г тем, что при его определении учитывается все время вынужденных простоев, тогда как при определении К_Г время простоя, связанное с проведением профилактических работ, не учитывается.

Суммарное время вынужденного простоя объекта обычно включает время:

• на поиск и устранение отказа;

• на регулировку и настройку объекта после устранения отказа;

• для простоя из-за отсутствия запасных элементов;

• для профилактических работ.

В некоторых объектах предусмотрены плановые отключения для проведения плановых ремонтов и технического обслуживания. Эти интервалы времени, как и интервалы, связанные с отключением по причине отказа, учитываются при определении анализируемых коэффициентов надежности.

В условиях эксплуатации на уровень надежности объектов большое влияние оказывают техническое обслуживание и ремонт.

Законы распределения, используемые при оценке надежности

Вероятностные модели оперируют случайными событиями, величинами и функциями.

При анализе надежности объектом исследования являются случайные события и величины. К случайным событиям относятся, как правило, отказы элементов, входящих в состав системы, а за случайную величину обычно принимают время работы объекта (время до возникновения отказа).

Функция плотности распределения f(t) служит полной характеристикой рассеивания сроков службы элементов. Кривая распределения f(t) – частота отказов – дает возможность подсчитать средний срок службы элемента (математическое ожидание), рассеивание (дисперсию) этих сроков службы относительно центра группирования и другие числовые параметры случайной величины T.

Закон распределения случайной величины определяется видом аналитических функций, описывающих показатели надежности, т.е. функциями P(t), f(t), λ(t).

Прежде чем приступить к инженерным методам расчета надежности и испытаний на надежность, следует рассмотреть закономерности, которым они подчиняются.

В теории надежности наибольшее распространение получили следующие законы распределения случайных величин: для дискретных случайных величин - биноминальный закон; закон Пуассона; для непрерывных случайных величин - экспоненциальный закон; нормальный закон; гамма-распределение; закон Вейбулла; закон Рэлея; логарифмически-нормальное распределение и др.

1. Биноминальный закон - распределение числа m появления события A в n независимых опытах (испытаниях). Если вероятность появления события A в одном испытании равна p, вероятность непоявления события A равна q=1-p, число независимых испытаний равно n, то вероятность появления m событий в испытаниях будет

(32)

где - число сочетаний из n по m.

Свойства распределения:

1. число событий n - целое положительное число;

2. математическое ожидание числа событий равно np;

3. среднеквадратическое отклонение числа событий .

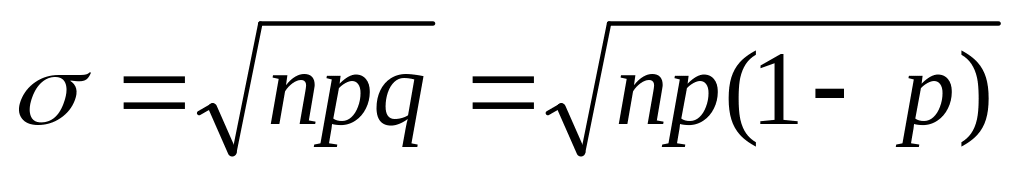При увеличении числа испытаний биноминальное распределение приближается к нормальному со средним значением и дисперсией .

2. Закон Пуассона - распределение случайного количества событий, которые появляются в фиксированном промежутке времени. Например, закон Пуассона используется, если необходимо определить вероятность того, что в изделии за заданное время t произойдет один, два, три и т.д. отказов.

Вероятность того, что за время t случайное событие произойдет k раз, вычисляется по формуле:

(33)

где a – параметр распределения Пуассона.

Свойства распределения:

1. математическое ожидание числа событий за время t равно а;

2. среднеквадратическое отклонение числа событий .

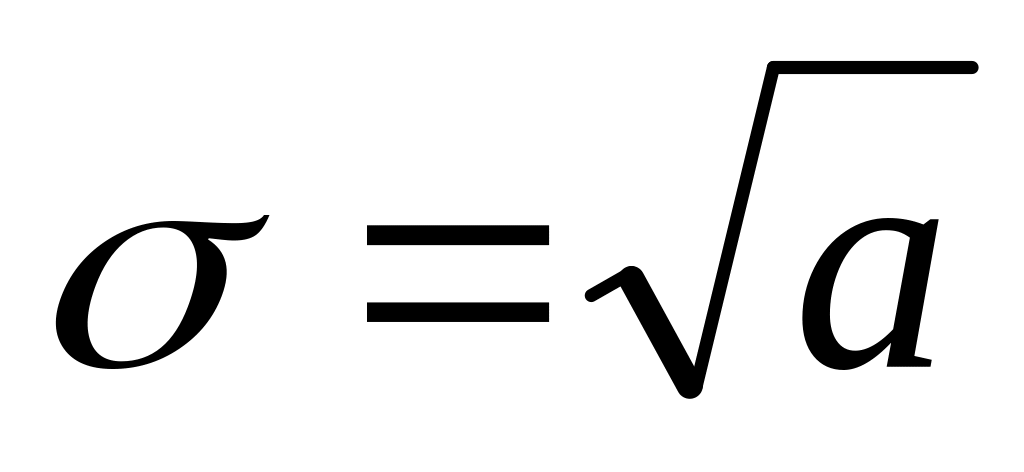Характерный признак распределения Пуассона - равенство математического ожидания и дисперсии. Это свойство используется для проверки степени соответствия исследуемого (опытного) распределения закону Пуассона.

Распределение Пуассона получается из биноминального распределения, если число испытаний n неограниченно возрастает, а математическое ожидание числа событий a=np остается постоянным.

Функция распределения F(x) распределения Пуассона имеет вид:

. Ее график приведен на рис.7.

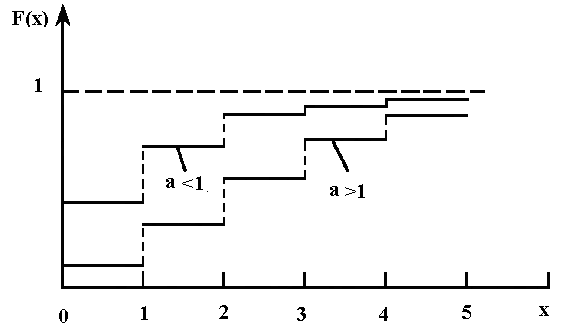
Рис. 7. Функция распределения Пуассона

Распределение Пуассона применяется для оценки надежности ремонтируемых изделий с простейшим потоком отказов:

(34)

где k – число отказов за время t; λ – интенсивность потока отказов; P_k(t) – вероятность того, что за время t произойдет k отказов.

Пример 1.

Среднее число отказов n_cp ремонтируемого устройства за время t₁ = 500 часов равно 10.

Какова вероятность того, что за время t₂ = 100 часов работы возникнет 2 отказа? 3 отказа?

; .

;

3. Экспоненциальный (показательный) закон распределения случайной величины Х задается плотностью вероятности f(x)=e^-x при x0,  - параметр экспоненциального распределения, =const.

Функция распределения величины Х определяется как

при x0.

Графики этих функций имеют вид (рис. 8 и 9):

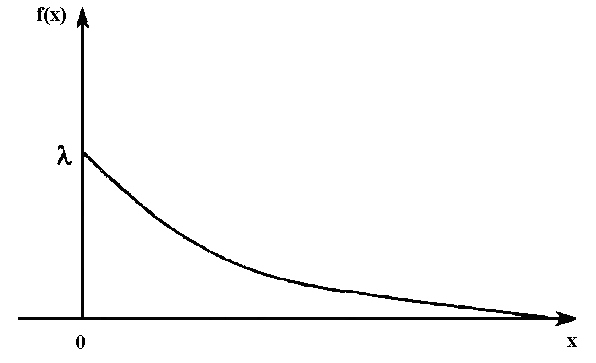
Рис. 8. Плотность экспоненциального распределения

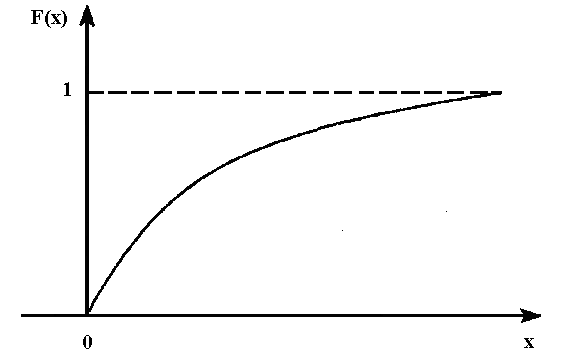
Рис. 9. Функция экспоненциального распределения

Свойства распределения:

1. математическое ожидание случайной величины равно ;

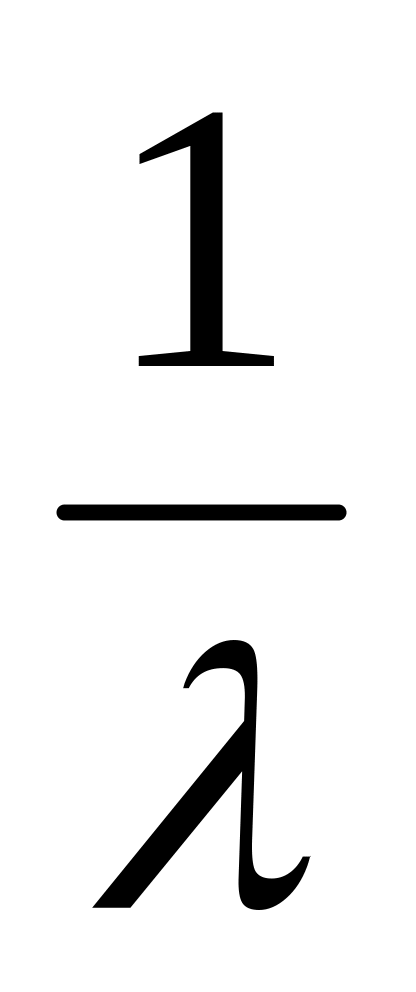2. среднеквадратическое отклонение случайной величины равно .

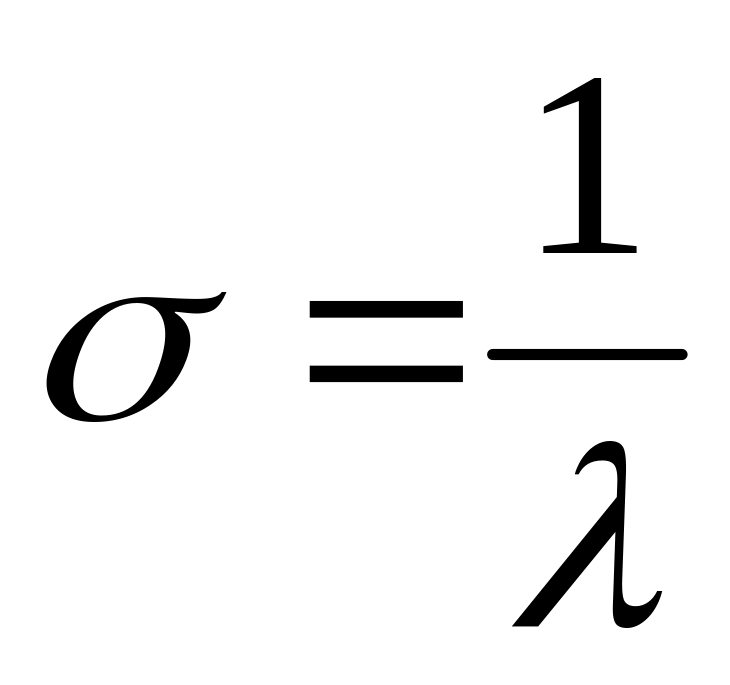Характерный признак экспоненциального распределения - равенство математического ожидания и среднего квадратического отклонения. Это свойство используется для проверки степени соответствия исследуемого (опытного) распределения экспоненциальному закону.

Статистические материалы об отказах элементов свидетельствуют о том, что в основном время их работы подчиняется экспоненциальному закону распределения. Условием возникновения экспоненциального закона распределения времени до отказа служит постоянство интенсивности отказов, что характерно для внезапных отказов на интервале времени, когда период приработки объекта закончился, а период износа и старения еще не начался, т.е. для нормальных условий эксплуатации.

Это распределение не учитывает износа элементов системы.

Экспоненциальное распределение типично для большинства сложных объектов, содержащих большое количество различных неремонтируемых элементов, имеющих преимущественно внезапные отказы из-за наличия скрытых дефектов. Данное распределение применяется также к ремонтируемым объектам с простейшим потоком отказов.

Время возникновения первичных отказов может быть расположено на оси времени так, что суммарный поток отказов сложного изделия становится близким к простейшему, т.е. с постоянной интенсивностью отказов.

Этими обстоятельствами, а также тем, что предположение об экспоненциальном распределении существенно упрощает расчеты надежности, объясняется широкое применение экспоненциального закона в инженерной практике.

Пусть Т – случайное время работы системы до отказа или наработка на отказ.

Тогда вероятность отказа за время t совпадает с функцией распределения этой случайной величины , т.е.

, (35)

где  - интенсивность отказов, а вероятность безотказной работы

, (36)

Функция f(t) есть плотность вероятности отказов и равна

(37)

Среднее время работы до возникновения отказа (или наработка на отказ) есть математическое ожидание случайной величины T и СКО и потому равно

. (38)

Отсюда (39)

График функции P(t) приведен на рис. 10.

Таким образом, зная среднее время безотказной работы Т₁ (или постоянную интенсивность отказов ), в случае экспоненциального распределения можно найти вероятность безотказной работы для интервала времени от момента включения объекта до любого заданного момента t.

Отметим, что вероятность безотказной работы на интервале, превышающем среднее время Т₁, при экспоненциальном распределении будет менее 0,368, так как Р(Т₁) = = 0,368.

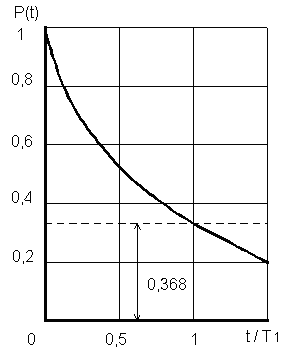
Рис. 10. График функции P(t) для экспоненциального распределения

Длительность периода нормальной эксплуатации до наступления старения может оказаться существенно меньше Т₁, то есть интервал времени, на котором допустимо пользование экспоненциальной моделью, часто бывает меньшим среднего времени безотказной работы, вычисленного для этой модели. Это легко обосновать, воспользовавшись дисперсией времени безотказной работы.

Из соотношения (38) для экспоненциального распределения дисперсия времени безотказной работы равна . Таким образом, наиболее вероятные значения наработки, группирующиеся в окрестности Т₁, лежат в диапазоне , то есть в диапазоне от t = 0 до t = 2Т₁. Как видим, объект может отработать и малый отрезок времени, и время t = 2Т₁, сохранив =const. Но вероятность безотказной работы на интервале 2Т₁ крайне низка: .

Важно отметить, что если объект отработал, предположим, время  без отказа, сохранив = соnst, то дальнейшее распределение времени безотказной работы будет таким, как в момент первого включения = соnst.

Таким образом, отключение работоспособного объекта в конце интервала  и новое его включение на такой же интервал множество раз приведет к пилообразной кривой   (см. рис. 11).

Другие распределения не имеют указанного свойства.

Модель экспоненциального распределения часто используется для априорного анализа, так как позволяет не очень сложными расчетами получить простые соотношения для различных вариантов создаваемой системы. На стадии апостериорного анализа (опытных данных) должна проводиться проверка соответствия экспоненциальной модели результатам испытаний. В частности, если при обработке результатов испытаний окажется, что , то это является доказательством экспоненциальности анализируемой зависимости.

Экспоненциальное распределение применяется для оценки надежности сложных систем, прошедших период "приработки", а также для систем, работающих под воздействием тяжелых механических и климатических нагрузок.

В большинстве случаев этот закон характерен для внезапных отказов и в тех случаях, когда вероятность безотказной работы системы в течение заданного периода времени не зависит от времени их работы, т.е. от положения периода Dt на оси времени эксплуатации.

На практике часто бывает, что   const, однако и в этом случае его можно применять для ограниченных отрезков времени. Это допущение оправдывается тем, что при ограниченном периоде времени переменную интенсивность отказов без большой ошибки можно заменить средним значением.

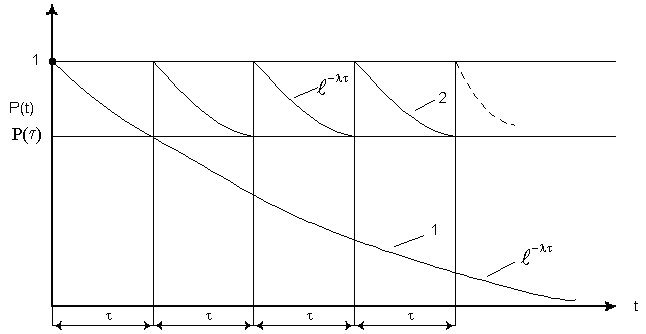
Рис. 11. Вероятность безотказной работы:

1 - непрерывная работа за время t, 2 - работа с интервалами .

Величина -процентного ресурса определяется из формулы P(t_)=0.01, так что

_.

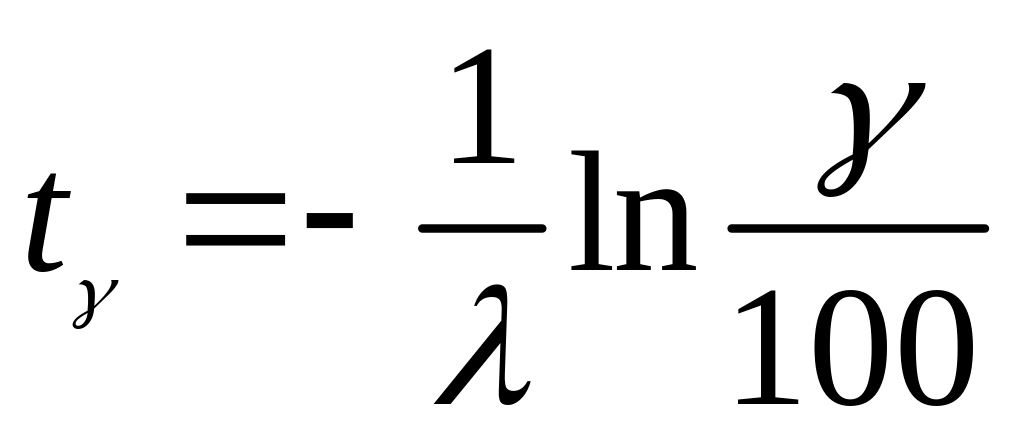С учетом (38) окончательно получим:

  .                               

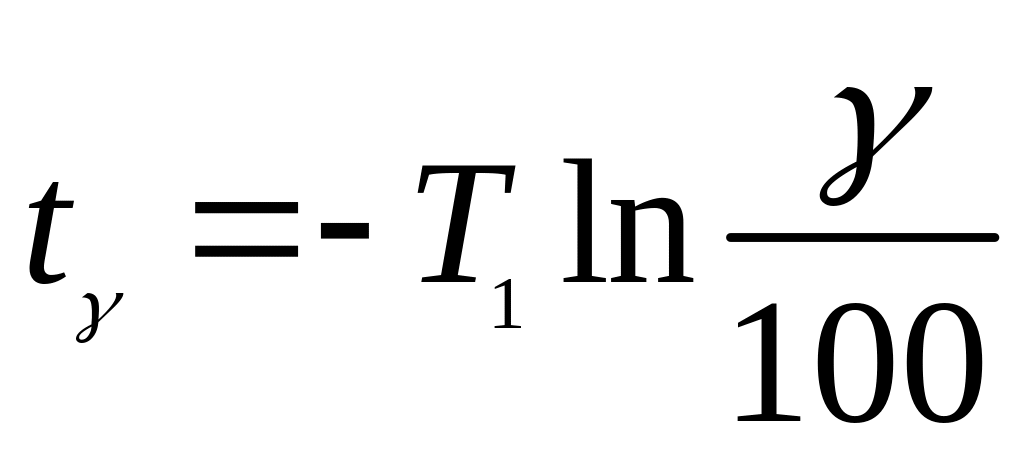Таким образом,  мы получили выражение, связывающее среднюю наработку до отказа T₁ и гамма-процентную наработку t_. Положим =90%. Это означает, что не менее 90% приборов от первоначально взятых должны безотказно работать в течение времени t_. Другими словами вероятность безотказной работы приборов в течение времени t_ должна быть не ниже 0.9, в то время как для средней наработки T₁ эта вероятность составляет всего лишь 0.37.

Таким образом, гамма-процентная наработка t_ при =90% равна

                                           

т.е. примерно составляет 0.1 от средней наработки до отказа.

Это означает, что при T₁=1000 часов вероятность безотказной работы на уровне 0.9 обеспечивается только на первых 100 часах. Или в партии на 100 приборов? имеющих T₁=1000 часов? через 100 часов останутся работоспособными 90, а через 1000 часов всего лишь 37 приборов будут работоспособными.

Следует отметить, что при t < < 1, т. е. при наработке t много меньшей, чем средняя наработка T₁, выражения для F(t), P(t), Q(t) можно упростить, заменив e^{-- t} двумя первыми членами разложения в степенной ряд.

Например, выражение для P(t) примет вид:

 

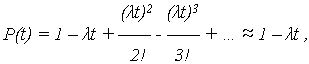
 при этом погрешность вычисления P(t) не превышает 0,5 ( t)².

Экспоненциальное распределение является частным случаем распределения Вейбулла при В = 1 и гамма-распределения при a=1 .

Пример 2.

Система состоит из двух устройств. Вероятности безотказной работы каждого из них в течение времени t = 100 часов равны соответственно P₁(100) = 0,95 и P₂(100) = 0,97. Найти среднее время работы системы до первого отказа при экспоненциальном законе надежности.

Решение.

Вероятность безотказной работы системы

Р(100)=Р₁(100)Р₂(100)=0,950,97= 0,92, т.е.

откуда λ = 0,83  10^-3 1/ч, а среднее время безотказной работы

Пример 3.

Время работы устройства до отказа подчинено экспоненциальному закону распределения с параметром λ = 2,5 · 10^-5 1/ч.

Определить количественные характеристики надежности устройства: вероятность безотказной работы P(t), вероятность отказа Q(t), частоту отказов f(t), наработку на отказ, если t = 2 000 часов.

Решение.

Используя выражение (7), вероятность безотказной работы в интервале времени от 500 ч до 2500 ч при условии, что объект проработал безотказно 500 ч, равна

4. Гамма-распределение. Плотность распределения гамма-распределения имеет вид:

, t0, a>0, >0 (40)

где Г(a) – Гамма-функция Эйлера

. (41)

a - параметр формы,  - масштабный параметр.

Вид гамма-распределения сильно зависит от значения его параметра a (рис. 12).

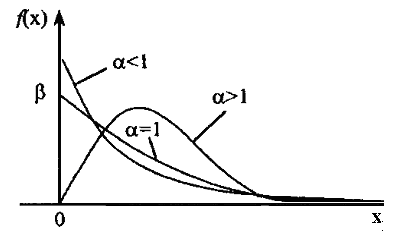
Рис. 12. Плотность гамма-распределения

Свойства распределения:

1. математическое ожидание случайной величины равно ;

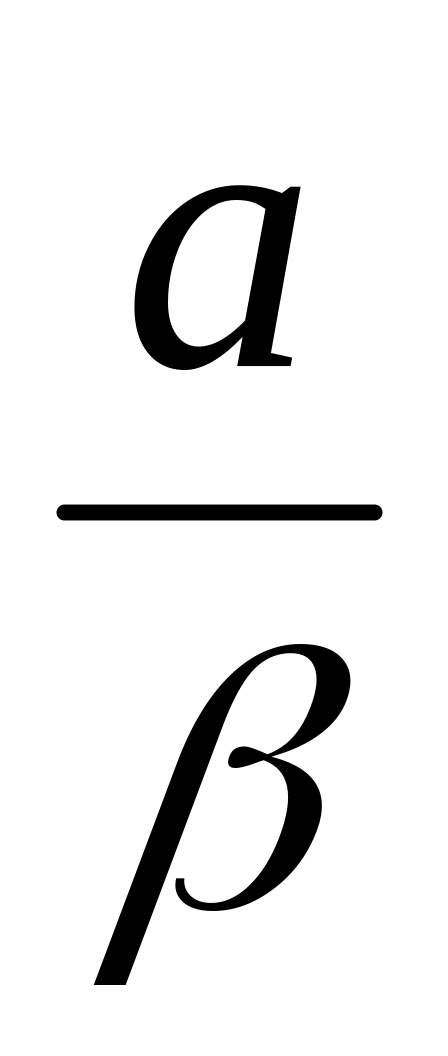2. среднеквадратическое отклонение случайной величины равно .

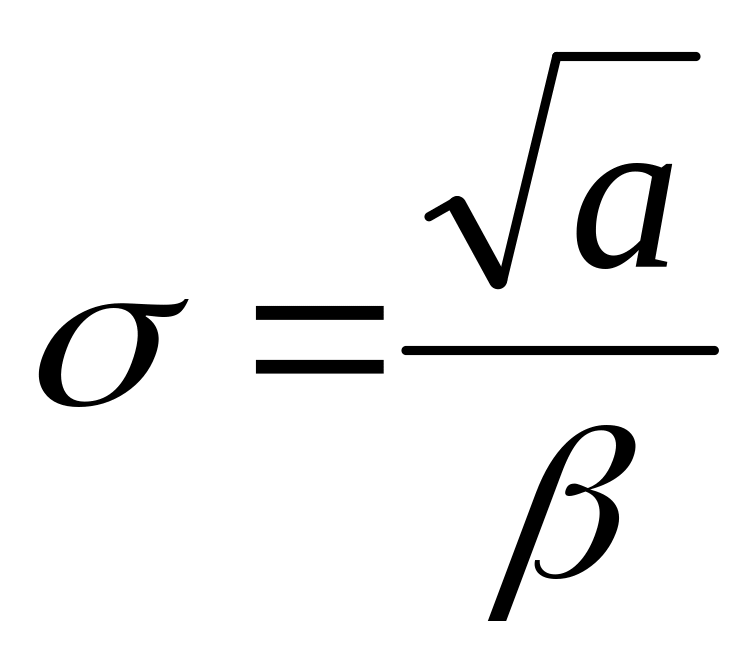Таким образом, числовые характеристики наработки до отказа имеют вид:

Среднее время работы устройства до отказа ,

дисперсия наработки до отказа . 

При a=1 получаем экспоненциальное распределение с параметром .

Гамма-распределение используется в теории надежности в качестве модели накапливающихся повреждений, если отказ устройства возникает тогда, когда произойдет не менее  отказов его элементов, а отказы элементов подчинены экспоненциальному закону с параметром .

Рис. 13. Графики изменения показателей надежности при гамма-распределении

При увеличении  -распределение будет приближаться к симметричному распределению - нормальному распределению с параметрами a = ·,  = ·², а интенсивность отказов будет иметь все более выраженный характер возрастающей функции времени.

Гамма-распределению подчиняется время работы резервированных устройств.

5. Распределение Вейбулла. Для случая, когда поток отказов не стационарный, т.е. плотность потока изменяется с течением времени, функция распределения времени до отказа приобретает вид, показанный на рис. 14.

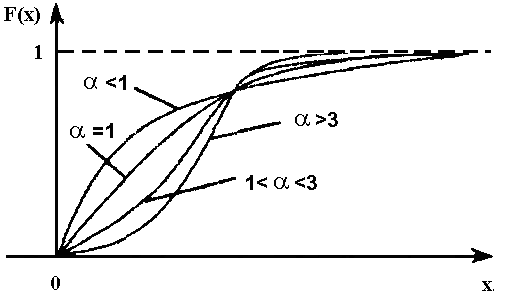
Рис. 14. Функция распределения Вейбулла

Согласно распределению Вейбулла, вероятность безотказной работы определяется по формуле

(42)

где λ₀ и  – параметры. Параметр ₀ определяет масштаб, при его изменении кривая распределения сжимается или растягивается;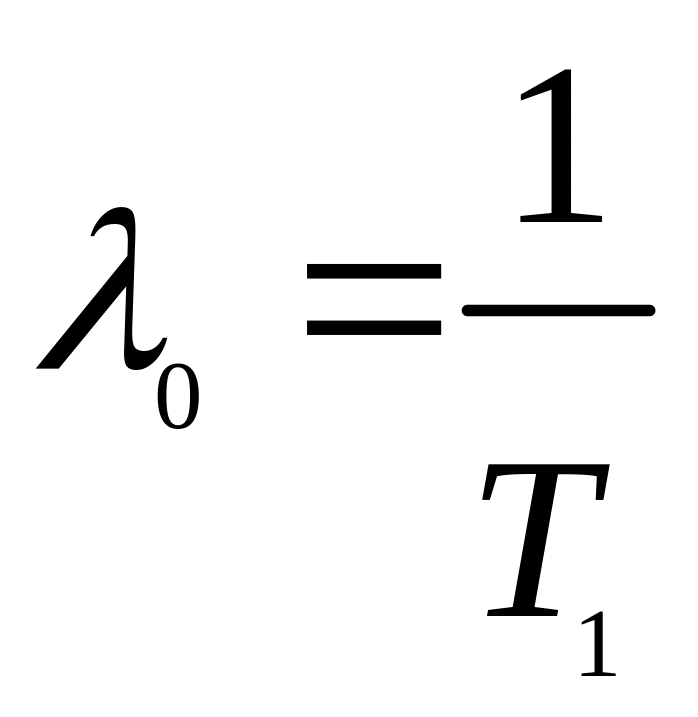 ;  - параметр формы (определяется подбором в результате обработки экспериментальных данных, > 0).

Частота отказов

(43)

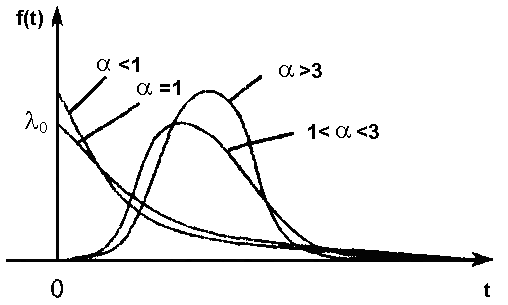
Рис.15. Плотность распределения Вейбулла

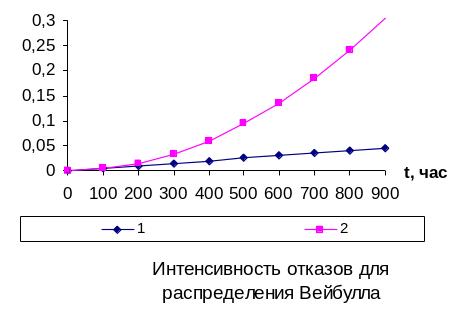
Интенсивность отказов

λ(t) = λ₀ ·  · t^-1. (44)

Опыт эксплуатации очень многих электронных приборов и значительного количества электромеханической аппаратуры показывает, что для них характерны три вида зависимостей интенсивности отказов от времени (рис. 16), соответствующих трем периодам жизни этих устройств.

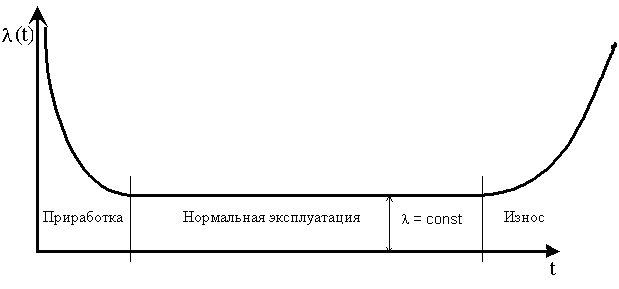
Рис. 16. Зависимость интенсивности отказов от времени

Нетрудно увидеть, что этот рисунок аналогичен рис. 3, так как график функции (t) соответствует закону Вейбулла. Указанные три вида зависимостей интенсивности отказов от времени можно получить, используя для вероятностного описания случайной наработки до отказа двухпараметрическое распределение Вейбулла. Особенностью распределения Вейбулла является то, что с изменением параметра  меняется характер зависимости показателя надежности от времени. Поведение системы на участке приработки хорошо описывается законом распределения Вейбулла с параметром  < 1, а на участке старения –  > 1.

При  = 1 функция распределения Вейбулла совпадает с экспоненциальным распределением; при  < 1 интенсивность отказов будет монотонно убывающей функцией; при  > 1 - монотонно возрастающей. Это обстоятельство дает возможность подбирать для опытных данных наиболее подходящие параметры  и ₀, с тем, чтобы уравнение функции распределения наилучшим образом совпадало с опытными данными, т.е. это распределение может быть использовано в качестве характеристики надежности, как в режиме приработки ( < 1), так и в режиме нормального функционирования ( = 1), так и в режиме старения ( >1).

При  = 2 распределение Вейбулла превращается в распределение Релея.

Распределение Вейбулла имеет место для отказов, возникающих по причине усталости тела детали или поверхностных. Этот случай связан с развитием усталостной трещины в зоне местной концентрации напряжений, технологического дефекта или начального повреждения. Период времени до зарождения микротрещины характеризуется признаками внезапного отказа, а процесс разрушения - признаками износового отказа.

Этот закон применим для отказов устройства, состоящего из последовательно соединенных дублированных элементов и других подобных случаев, может быть использовано при ускоренных испытаниях элементов в форсированных режимах.

Средняя наработка до первого отказа определится из следующего выражения:

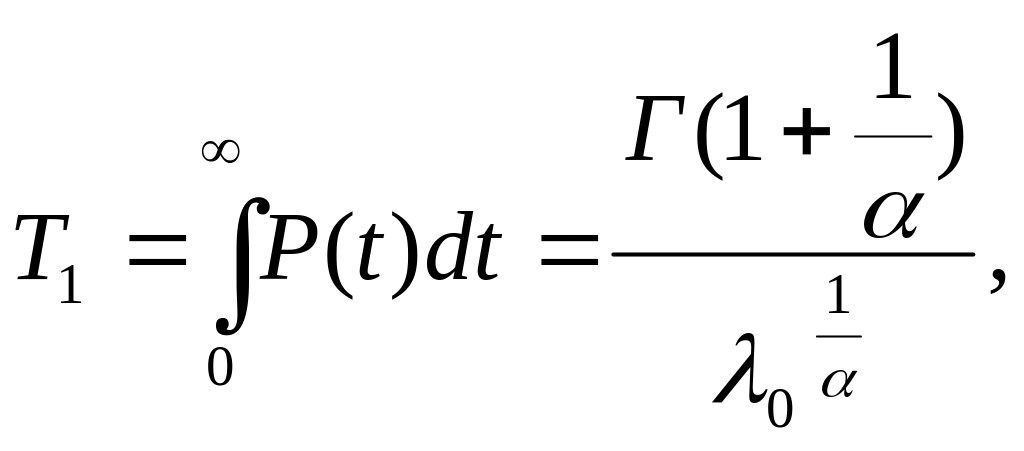(45)

где – табулированная гамма-функция.

Среднее квадратическое отклонение

Пример 4.

Время безотказной работы объекта подчиняется закону Вейбулла с параметрами  = 1,5; время работы t = 100 часов.

Определить вероятность безотказной работы P(t), частоту отказов f(t), интенсивность отказов λ(t), среднее время безотказной работы Т₁.

Решение.