2. Тесты, позволяющие выявить наличие гетероскедастичности остатков

Обнаружение гетероскедастичности в каждом конкретном случае является довольно сложной задачей, так как для знания дисперсий отклонений необходимо знать распределение СВ Y, соответствующее выбранному значению СВ Х.

Не существует какого-либо однозначного метода определения гетероскедастичности. Однако к настоящему времени для такой проверки разработано довольно большое число тестов и критериев для них. Рассмотрим наиболее популярные и наглядные: графический анализ отклонений, тест ранговой корреляции Спирмена, тест Парка, тест Глейзера, тест Гольдфельда-Квандта.

1).Графический анализ остатков.

Использование графического представления отклонений позволяет определиться с наличием гетероскедастичности. В этом случае по оси абсцисс откладываются значения объясняющей переменной Х (либо линейной комбинации объясняющих переменных , а по оси ординат либо отклонения , либо их квадраты . Примеры таких графиков приведены на рис. 5.3.

На рис. 5.3,а все отклонения находятся внутри полуполосы постоянной ширины, параллельной оси абсцисс. Это говорит о независимости дисперсий от значений переменной Х и их постоянстве, т.е. в этом случае выполняются условия гомоскедастичности.

На рис. 5.3, б-д наблюдаются некоторые систематические изменения в соотношениях между значениями переменной Х и квадратами отклонений . Рис. 5.3, б соответствует примеру из пункта 1. На рис. 5.3, в отражена линейная, 5.3, г – квадратичная, 5.3, д – гиперболическая зависимости между квадратами отклонений и значениями объясняющей переменной Х. Другими словами, ситуации, представленные на рис. 5.3, в-д, отражают большую вероятность наличия гетероскедастичности для рассматриваемых статистических данных.

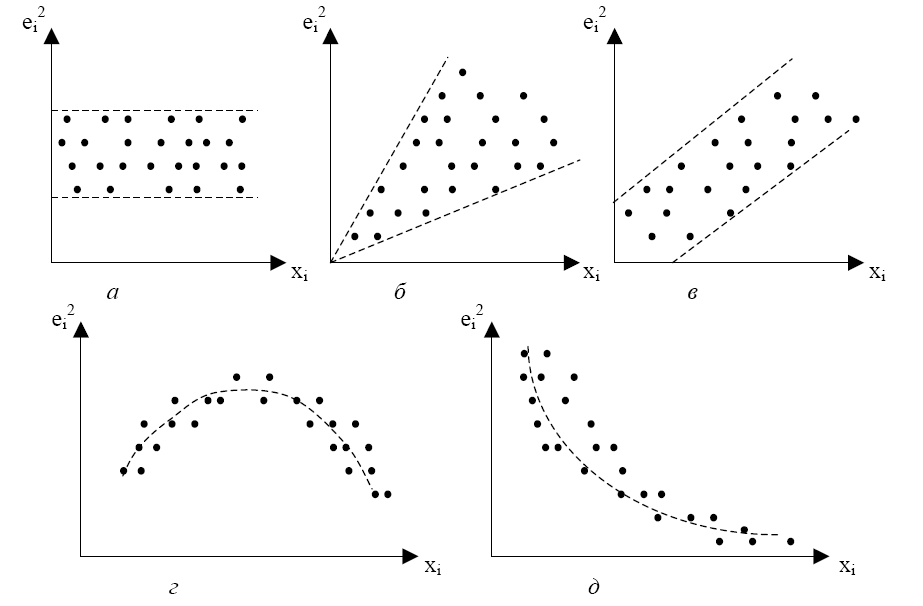
Рис. 5. 3

2).Тест ранговой корреляции Спирмена

При использовании данного теста предполагается, что дисперсия отклонения будет либо увеличиваться, либо уменьшаться с увеличением значений Х. Поэтому для регрессии, построенной по МНК, абсолютные величины отклонений и значения СВ Х будут коррелированны. Значения и ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:

, (5.1)

где - разность между рангами и ; -число наблюдений.

Например, если является 25-м по величине среди всех наблюдений Х, а является 32-м, то .

Доказано, что если коэффициент корреляции для генеральной совокупности равен нулю, то статистика

(5.2)

имеет распределение Стьюдента с числом степеней свободы .

Следовательно, если наблюдаемое значение -статистики, вычисленное по формуле (5.2), превышает (определяемое по таблице критических точек распределения Стьюдента), то необходимо отклонить гипотезу о равенстве нулю коэффициента корреляции , а следовательно, и об отсутствии гетероскедастичности. В противном случае гипотеза об отсутствии гетероскедастичности принимается.

3).Тест Парка.

Р.Парк предложил критерий определения гетероскедастичности, дополняющий графический метод некоторыми формальными зависимостями. Предполагается, что дисперсия является функцией -го значения объясняющей переменной. Парк предложил следующую функциональную зависимость:

. (5.3)

Прологарифмировав (5.3), получим:

. (5.4)

Так как дисперсия обычно неизвестны, то их заменяют оценками квадратов отклонений .

Критерий Парка включает следующие этапы:

1. Строится уравнение регрессии .

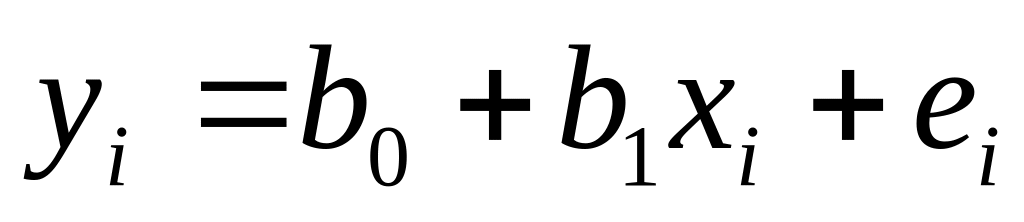2. Для каждого наблюдения определяются .

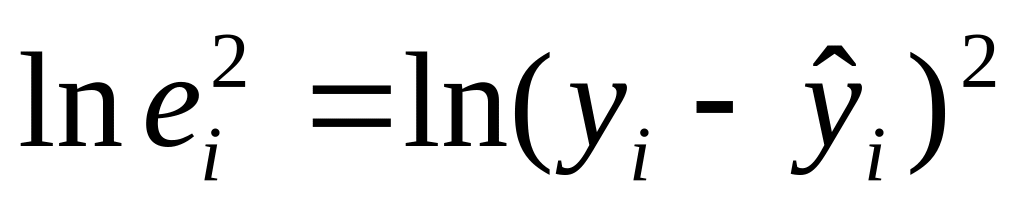3. Строится регрессия

, (5.5)

где .

В случае множественной регрессии зависимость (5.5) строится для каждой объясняющей переменной.

4. Проверяется статистическая значимость коэффициента уравнения (5.5) на основе -статистики 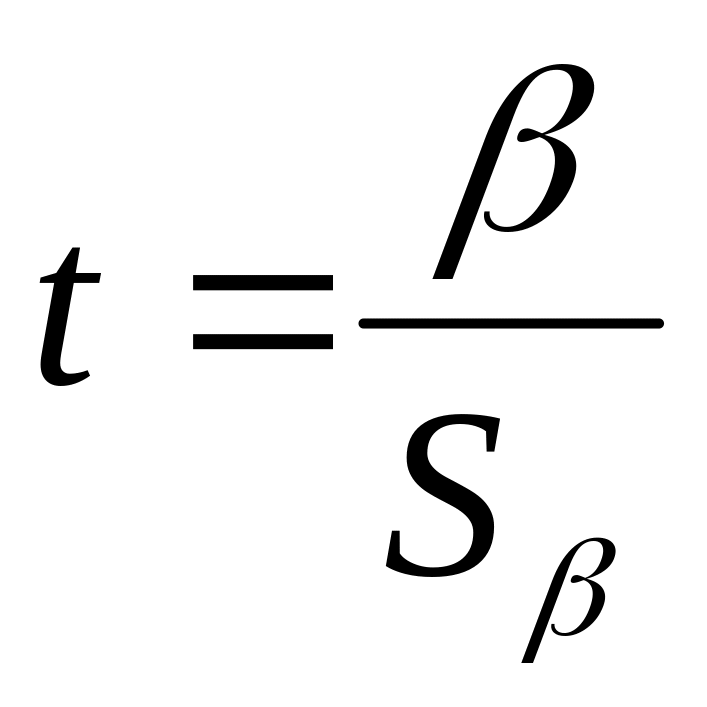. Если коэффициент статистически значим, то это означает наличие связи между 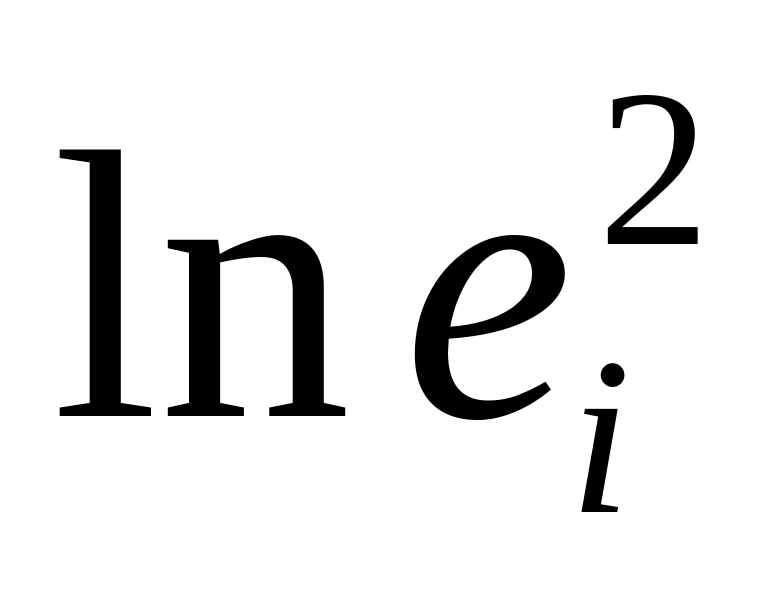и , т.е. гетероскедастичности в статистических данных.

4).Тест Глейзера.

Тест Глейзера по своей сути аналогичен тесту Парка и дополняет его анализом других (возможно, более подходящих) зависимостей между дисперсиями отклонений и значениями переменной . По данному методу оценивается регрессионная зависимость модулей отклонений (тесно связанных с ) от . При этом рассматриваемая зависимость моделируется следующим уравнением регрессии:

. (5.6)

Изменяя значение , можно построить различные регрессии. Обычно Статистическая значимость коэффициента в каждом конкретном случае фактически означает наличие гетероскедастичности. Если для нескольких регрессий (5.6) коэффициент оказывается статистически значимым, то при определении характера зависимости обычно ориентируются на лучшую из них.

5).Тест Гольдфельда-Квандта.

В данном случае также предполагается, что стандартное отклонение пропорционально значению переменной Х в этом наблюдении, т.е. . Предполагается, что имеет нормальное распределение и отсутствует автокорреляция остатков.

Тест Гольдфельда-Квандта состоит в следующем:

1. Все наблюдений упорядочиваются по величине Х.

2. Вся упорядоченная выборка после этого разбивается на три подвыборки размерностей 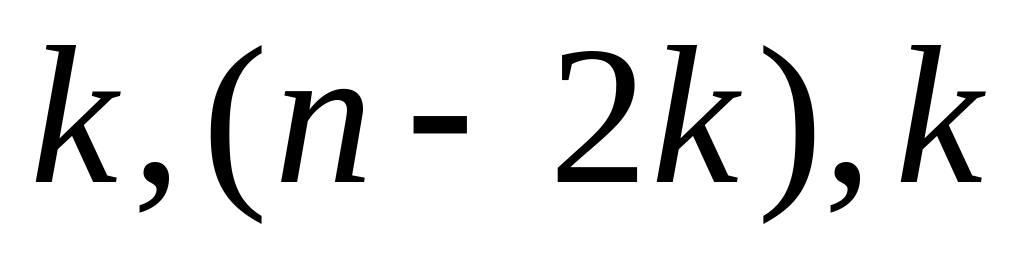соответственно.

3. Оцениваются отдельные регрессии для первой подвыборки ( первых наблюдений) и для третьей подвыборки ( последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям Х верно, то дисперсия регрессии по первой подвыборке (сумма квадратов отклонений 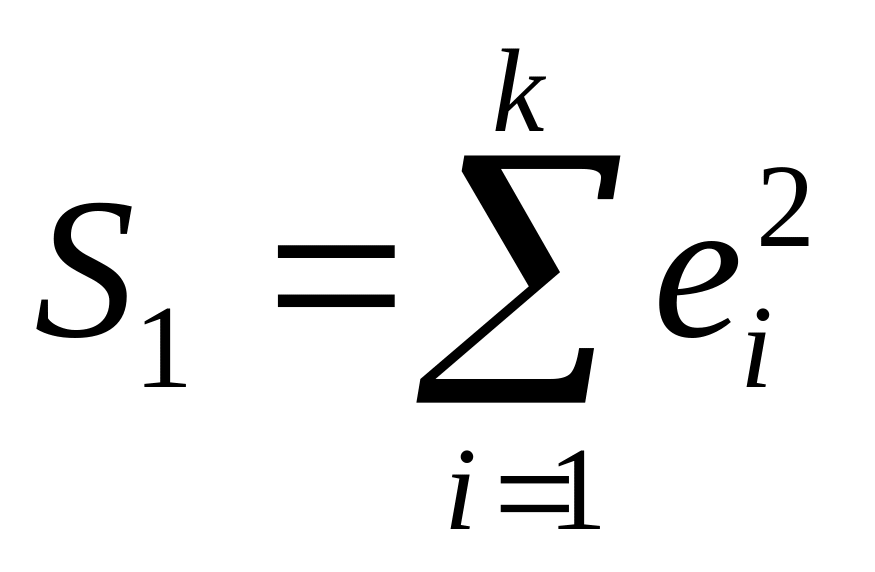) будет существенно меньше дисперсии регрессии по третьей подвыборке (суммы квадратов отклонений ).

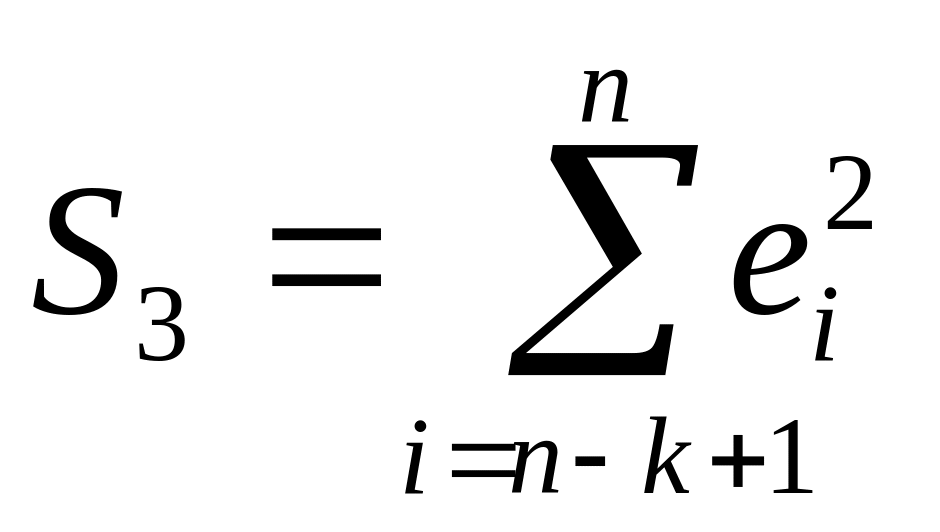4. Для сравнения соответствующих дисперсий строится следующая -статистика:

. (5.7)

Здесь - число степеней свободы соответствующих выборочных дисперсий ( - количество объясняющих переменных в уравнении регрессии).

При сделанных предположениях относительно случайных отклонений построенная -статистика имеет распределение Фишера с числами степеней свободы .

5. Если , то гипотеза об отсутствии гетероскедастичности отклоняется (здесь - выбранный уровень значимости).

Естественным является вопрос: какими должны быть размеры подвыборок для принятия обоснованных решений? Для парной регрессии Гольдфельд и Квандт предлагают следующие пропорции: .

Для множественной регрессии данный тест обычно проводится для той объясняющей переменной, которая в наибольшей степени связана с . При этом должно быть больше, чем . Если нет уверенности относительно выбора переменной , то данный тест может осуществляться для каждой из объясняющих переменных.

Этот же тест может быть использован при предположении об обратной пропорциональности между и значениями объясняющей переменной. При этом статистика Фишера примет вид: .