§17.Определение производной

Определение. Пусть - некоторая величина, которую назовем приращением аргумента. Тогда назовем приращением функции.

Определение. Производной от функции в точке х называется предел

Производная обозначается или , или или и т.д.

Определение. Если производная (существует и) конечна, то функция называется дифференцируемой.

Пример 17.1. Вычислим (пользуясь определением) производную функции . =Ш= =

= = .

§18.Геометрический смысл производной

Теорема. Производная от функции в точке равна угловому коэффициенту касательной к кривой , проведенной в точке Уравнение касательной имеет вид: .

Пример 18.1. Найдем уравнение касательной к графику функции в точке :

уравнение касательной или (см. рис. 18.1)

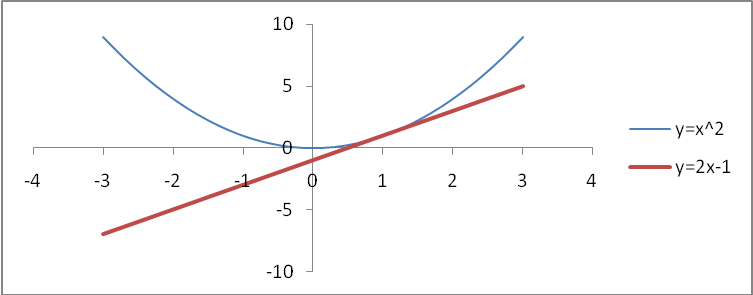
Рис. 18.1.

§19.Производная от постоянной величины

Теорема. Производная от постоянной величины равна нулю. Т.е.

Пример 19.1.

§20.Производная от степенной функции

Теорема. Если то

Пример 20.1. =Ш= =

§21.Производная суммы

Теорема. Если существуют (конечные) производные функций и , то существует производная суммы (разности) этих функций и

Пример 21.1.

Пример 21.2. 10 и 8=

=

§22.Производная от произведения функций

Теорема. Если существуют (конечные) производные и то существует производная от произведения этих функций и .

Пример 22.1.

=§20, §21, Ш =

§23.Производная частного

Теорема. Если существуют (конечные) производные и и , то существует производная от частного этих функций и

Пример23.1. = Ш=

§24.Производные от тригонометрических функций

Теорема. Справедливы следующие формулы:

Пример 24.1. =§23=

= = =

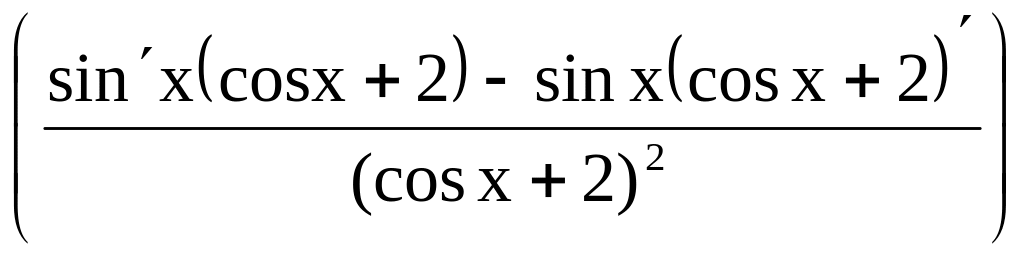=Ш=

§25.Производная сложной функции

Определение. Если а то называется сложной функцией.

Замечание. Аргумент будем называть зависимым аргументом, а - независимым аргументом. Но в формуле мы предполагаем, что производная определена, когда - независимый аргумент.

Теорема. Если существуют (конечные) производные и , то существует производная и

Пример 25.1. Если х независимый аргумент, то из §21 следует Аналогично , если u является независимым аргументом. Формула не всегда удобна, т.к. здесь нужно подразумевать, что х – независимый аргумент. Но если чуть поправить , то мы получим универсальную формулу. В литературе, как правило, она приводится в следующем виде . Буквой х, как правило (но не всегда), обозначается независимый аргумент.

Пример 25.2. обозначим = = = 9 и 7=

§26.Производная от логарифмической функции

Теорема.

Пример 26.1.

обозначим = =13=

=

= обозначим = 19=

= = = 8 и 6 =

=

§27.Производная от показательной функции

Теорема.

Пример 27.1. 12= =

= 21 и 15 = = = 9 и 7 =

=

§28.Производные от обратных тригонометрических функций

Теорема.

Пример 28.1.

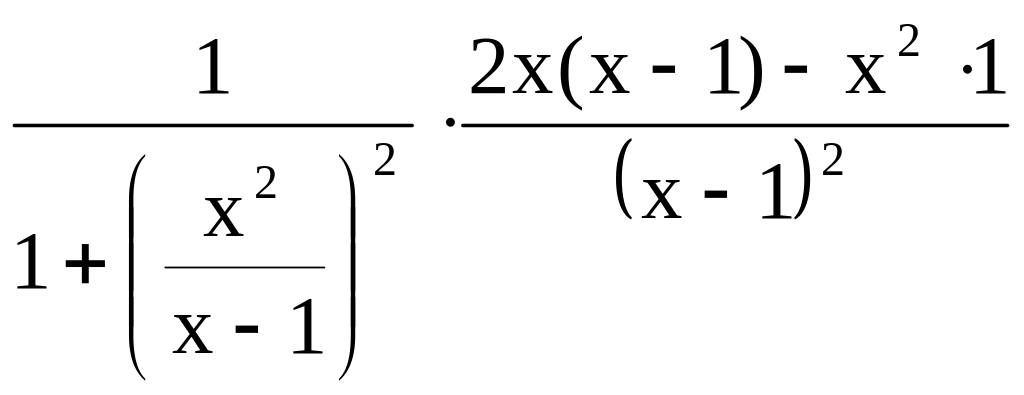25, 12, 8 = = =Ш=

= .

§29.Дифференциал

Если функция дифференцируема в точке х, т.е. имеет в этой точке конечную производную , то , где при отсюда

Определение. Главная часть приращения функции, линейная относительно , называется дифференциалом функции и обозначается

Теорема 29.1. Если х – независимый аргумент, то

Теорема 29.2. Запись дифференциала не зависит от того, является ли независимым аргументом, или функцией от другого аргумента. Это свойство называется инвариантностью первого дифференциала.

Пример 29.1.

Пример 29.2. Если , то = =

= = .

§30.Свойства дифференциала функции

Теорема. 1. 2. . 3. 4. 5. (Самостоятельно уточните формулировки этих формул).

§31.Производные различных порядков.

Определение. Производная от первой производной называется второй производной и обозначается или или Аналогично определяются производные третьего и так далее порядков.

Пример 31.1.

. Теперь легко догадаться, что (Обратите внимание, как обозначается производные).

§32.Дифференциалы различных порядков

Определение. Дифференциал от дифференциала первого порядка называется дифференциалом второго порядка и обозначается . Аналогично определяются дифференциалы третьего и т.д. порядков. Обозначим .

Теорема. Если - независимый аргумент, то ...; .

Пример 32.1.

§33.Свойства непрерывных функций

Теорема 33.1.(Теорема Больцано-Коши; чеш. математик и философ 1781-1848; франц. математик 1789-1857). Пусть функция определена и непрерывна на отрезке и Тогда существует точка такая, что

Пример 33.1. Пусть Очевидно, что Поэтому можно утверждать, что на интервале (0;4) график данной функции хотя бы один раз пересекает ось абсцисс. (В действительности три раза пересекает ось абсцисс при х=1, х=2, х=3, рис. 33.1).

Теорема 33.2. (Теорема Вейерштрасса; нем. математик 1815-1897). Пусть функция определена и непрерывна на отрезке . Тогда ограничена на этом отрезке.

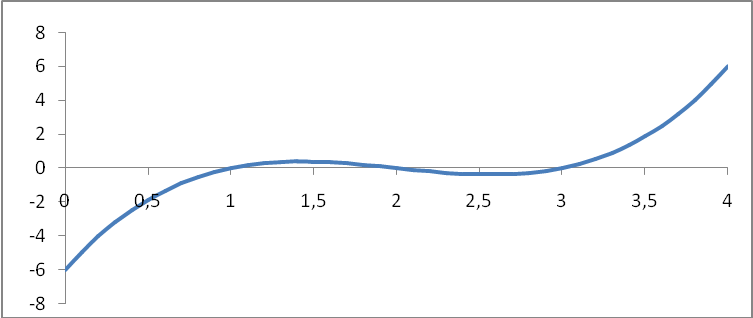Рис. 33.1.

Пример 33.2. На рис. 33.1 дан график функции . Функция на отрезке [0,4] непрерывна. Значит на интервале (0,4) она не может принимать сколь угодно большие значения.

Теорема 33.3. (Теорема Ролля; франц. математик 1652-1719). Пусть функция определена и непрерывна на отрезке , дифференцируема в каждой точке интервала и . Тогда существует точка такая, что

Пример 33.1. На рисунке 33.3 дан график функции

Рис. 33.3.

Т.К. функция непрерывна на отрезке [3,5], диффуренцируема внутри этого отрезка и . Поэтому внутри отрезка [3,5] найдется по крайней мере одна точка, в которой касательная горизонтальна.