Касательные напряжения при изгибе. Формула д. И. Журавского для определения касательных напряжении при изгибе

Так как внутренние усилия при поперечном изгибе балки при­водятся к изгибающему моменту и поперечной силе, то балка помимо изгиба испытывает сдвиг (срез) и, следовательно, в ее сечениях кроме нормальных возникают и касательные напряжения.

По закону взаимности касательных напряжений, действие их по какой-либо площадке вызывает равные по величине, но противопо­ложные по знаку касательные напряжения по площадке, перпенди­кулярной к первой. Следовательно, по площадкам, параллельным нейтральному слою, должны действовать касательные напряжения, что полностью подтверждается опытами.

Рассмотрим, например, балку, составленную из двух одинаковых брусьев прямоугольного сечения (рис. 7, а), причем допустим, что трение между ними отсутствует. Пусть эта балка изгибается под дейст­вием сосредоточенной силы Р, приложенной к середине пролета. После деформации балка примет вид согласно рис. 7, б, т. е. каждый брус изогнется независимо друг от друга. Поэтому нижние волокна каждого бруса будут растягиваться, а верхние – сжиматься. По плоскости соприкасания они будут скользить один по другому, а их концевые сечения, лежавшие до деформации в одной плоскости, разойдутся.

На практике, в случае применения составных деревянных балок, скольжение между брусьями устраняется при помощи шпонок, изго­товляемых обычно из твердых пород дерева (рис. 7, б). Наблюдения за зазорами у шпонок (рис. 7, в) позволяют определить направление скольжения в составной балке и, следовательно, направление касательных напряжений, действующих в нейтральном слое цельной балки. Цельная балка под действием силы изогнется так, как показано на рис. 8. При этом волокна АВ будут лежать в нейтральном слое и, следовательно, длина их останется без изменения. Значит, при изгибе цельной балки по нейтральному слою от одной половины балки на другую передаются касательные напряжения ^’ = , не допускающие сдвига верхней половины относительно нижней (рис. 8, а).

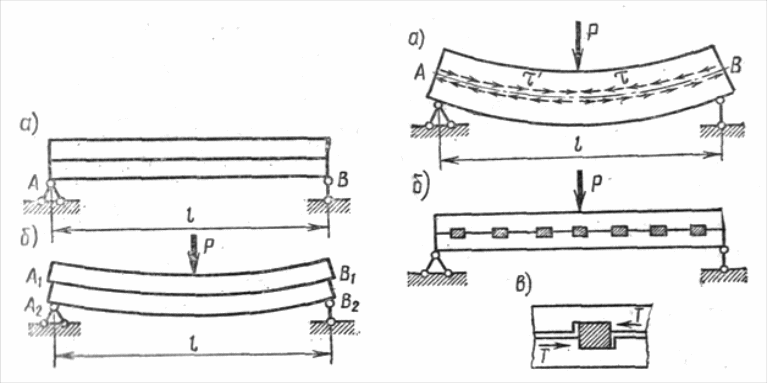Рис. 7. Рис. 8.

Действие продольных касательных напряжений при изгибе балок было впервые правильно оценено Д. И. Журавским, который также разработал и теорию касательных напряженней при изгибе балок прямоугольного сечения. Им же были сделаны следующие основные допущения при изучении этой теории: а) касательные напряжения в каждой точке поперечного сечения направлены параллельно поперечной силе Q; б) касательные напряжения распределяются равномерно по ширине поперечного сечения балки.

Указанные допущения приняты в сопротивлении материалов в целях упрощения вывода формулы для определения величины касательных напряжений и закона распределения их по высоте сечения балки. Для балок прямоугольного сечения, когда их высота больше ширины, указанные допущения очень близки к действительности.

Касательные напряжения определяются по формуле Д. И. Ж у р а в с к о г о:

где  – касательное напряжение на площадке, параллельной нейт­ральному слою;

q – поперечная сила в рассматриваемом сечении балки;

I_x – момент инерции относительно нейтральной оси всего поперечного сечения балки;

S_x – статический момент относительно нейтральной оси той части поперечного сечения, которая лежит выше или ниже рассматриваемой площадки;

b – ширина сечения на уровне площадки, по которой опреде­ляются касательные напряжения.

Кривая, в которую обращается первоначальная ось балки под дей­ствием внешних сил, называется изогнутой осью балки, или упругой линией (рис. 9).

Прогибы в разных сечениях различны и зависят от расстояния z от принятого начала координат, например, совпадающего с точкой А, т. е. у_z = f₁ (z). При z = 0 у_z = 0, а при z = он достигает наиболь­шего своего значения, т. е. у_тах – f, где f – наибольший прогиб.

Оси координат условимся располагать следующим образом.

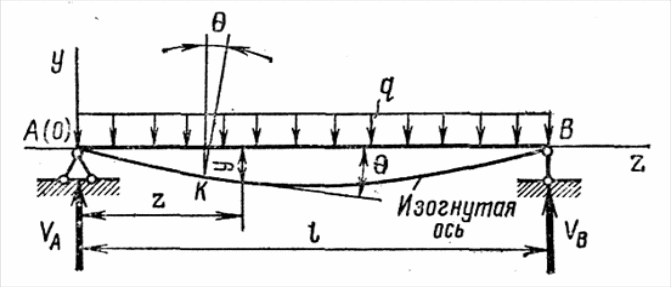
Рис. 9.

Начало координат примем на левом конце балки, ось z направим вправо по оси балки, а ось у – вверх. Такое расположение осей коор­динат даст возможность считать прогибы балки вниз отрицательными, а прогибы вверх – положительными.

Угол, составленный, касательной к любой точке k изогнутой оси с первоначальным ее положением, условимся обозначать  (тетта). На основании гипотезы плоских сечений, пренебрегая ис­кривлением сечений бал­ки при поперечном из­гибе, будем считать, что поперечное сечение бал­ки, проведенное через произвольную точку k первоначальной оси, по­ворачивается при из­гибе балки на тот же угол . Следовательно, угол  выражает угловое перемещение попе­речного сечения балки при изгибе и называется углом пово­рота сечения балки. Он равен первой производной по z от прогиба в этом сечении, т. е.  = у'.

Во многих случаях принятые сечения балки, хотя и удовлетворяют требованию прочности, но балка недостаточно жестка, т. е. изогнутая ось имеет излишне большую кривизну, и прогибы их превышают допустимые пределы, установленные нормами проектирования. По­этому, если задан допускаемый прогиб для балки, необходимое поперечное сечение подбирают из условия жесткости.

Кроме расчета балок, ферм и других конструкций на жесткость, изучение деформаций изгибаемых балок необходимо еще для решения статически неопределимых задач при изгибе, когда требуется в допол­нение к уравнениям статики составлять недостающие уравнения из условий деформации оси балки.

Для определения изогнутой оси балки необходимо составить ее уравнение, т. е. выразить ординаты (прогибы балки) в функции от положения точек по длине балки, другими словами, найти зависимость у = f (z). Чтобы найти эту зависимость, используем равенство

и выражающее связь кривизны балки с изгибающим моментом и попе­речной жесткостью сечения.

Формула кривизны, получаемая из высшей математики, выражает ее связь с производными у' и у" от ординат кривой:

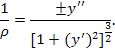
Зависимость эту можно упростить, имея в виду, что прогибы балок очень малы по сравнению с длиной балки, а углы наклона также не составляют величины, большей 1°. В знаменатель же правой части этой формулы входит (y^’)² – тангенс угла наклона в квадрате, являю­щийся малой величиной по сравнению с другой величи­ной, входящей в двучлен знаменателя, а поэтому ее отбрасывают, в результате чего формула принимает вид

т. е. кривизна балки приближенно равна второй производной от про­гиба. Теперь формулу можно представить так:

Напомним из математики, что знак второй производной зависит от направления осей координат, а именно: она будет иметь положитель­ное значение, если вогнутость кривой направлена в сторону положи­тельной оси, и, наоборот, будет отрицательной, если в сторону поло­жительной оси направлена выпуклость кривой (рис. 10, а, б). Изги­бающий момент, как мы условились, в первом случае будет положи­телен, во втором – отрицателен.

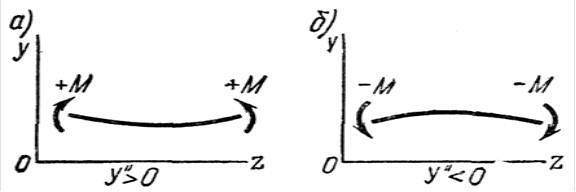
Рис. 10.

Таким образом, при направлении оси у вверх в уравнении нужно оставить знак плюс, а при направлении оси у вниз – знак минус.

В дальнейшем будем направлять ось у всегда вверх, тогда дифферен­циальное уравнение примет вид:

Полученное уравнение называется приближенным дифференциальным уравнением изогнутой оси балки.