Тема №8. Определение напряжений

Если на поверхность призматического стержня нанести сетку линий, параллельных и перпендикулярных оси стержня (рис. 8.1, а), и приложить к нему растягивающую силу, то можно убедиться в том, что линии сетки и после деформации останутся взаимно перпендикулярными, за исключением небольшого участка стержня вблизи точки приложения силы, который из рас­смотрения пока исключаем, но расстояния между ними изме­нятся (рис. 8.2, б). Все горизонтальные линии, например cd, переместятся вниз, оставаясь горизонтальными и прямыми. Можно предположить также, что и внутри стержня будет такая же картина, т. е. поперечные сечения стержня, плоские и нор­мальные к его оси до деформации, останутся плоскими и нор­мальными к оси и после деформации.

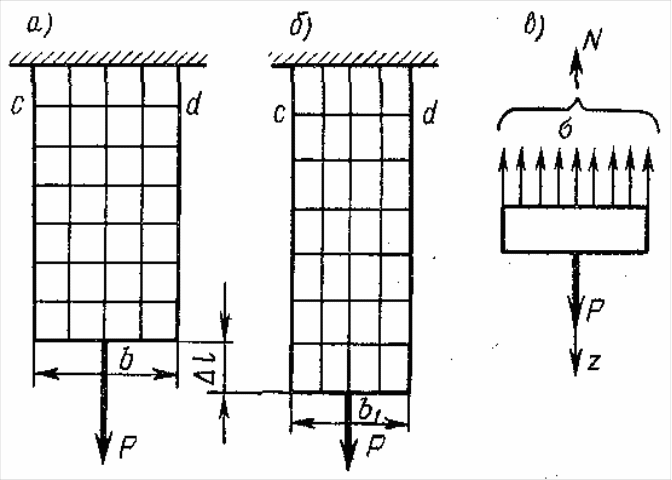
Рис. 8.1.

Эту гипотезу называют гипотезой плоских сечении или гипо­тезой Бернулли. Формулы, полученные на основе этой гипотезы, подтверждаются результатами опытов. Такая картина деформаций дает основание считать, что в поперечных сечениях стержня действуют только нормальные напряжения, равномерно распределенные по сечению, а каса­тельные напряжения равны нулю.

Продольная сила N есть равнодействующая нормальных напряжений в поперечном сечении:

N =  dF.

Поскольку  = const, получим N = ∙F, откуда ;

В частном случае, когда на стержень действует одна внеш­няя сила Р, из уравнения равновесия получим N = Р (рис. 8.1, в) и вместо общей формулы получим частный вид форму­лы для растяжения

;

Эти формулы справедливы и для сжатия, с той только разни­цей, что сжимающие напряжения считаются отрицательными.

Кроме того, сжатые стержни помимо расчета на прочность рассчитываются также на устойчивость.

Тема №9. Определение деформаций и перемещений

Для многих материалов при нагружении до определенных пределов опыты показывают следующую зависимость между относительным удлинением стержня  и напряжением :

;

Эта зависимость носит название закона Гука и формулирует­ся следующим образом:

линейные деформации прямо пропорциональны нормальным напряжениям.

В формуле Е — коэффициент, зависящий от материала и называемый модулем продольной упругости или модулем упру­гости первого рода (модуль Юнга). Он характеризует жесткость материала, т. е. его способность сопротивляться деформированию.

Поскольку  – безразмерная величина, то из формулы видно, что единица Е та же, что и , т. е. паскаль (Па).

Имея в виду, что для стержня постоянного сечения , а то можно получить формулу для определения полного (абсолютного) удлинения (укорочения) стержня:

; – закон Гука при удлинении.

Между продольной  и поперечной ' деформациями су­ществует установленная экспериментально зависимость

' = –∙;

Здесь  – коэффициент поперечной деформации (коэффициент Пуассона), характеризующий способность материала к попе­речным деформациям. Удли­нение считается положительным, укорочение — отрицательным.