Метод начальных параметров

Решение дифференциального уравнения изогнутой оси балки заклю­чается в составлении такой формы уравнения, из которого можно было бы получить непосредственную связь между прогибами y и абсциссой z.

Аналитический метод решения состоит в двукратном интегрирова­нии дифференциального уравнения, в результате которого первое интегрирование дает уравнение углов поворота

а второе интегрирование – уравнение прогибов

После каждого интегрирования получаем постоянную интегриро­вания. Таким образом, для каждого участка балки в результате двух­кратного интегрирования уравнения изогнутой оси получают две постоянные интегрирования.

Постоянные интегрирования опре­деляют из условий закрепления балки (опорных условий), а также из усло­вий на границах смежных участков (граничных условий). При этом:

а) каждая неподвижная или подвижная опора дает одно условие – равенство нулю прогиба в сечении балки на опоре;

б) от каждой жесткой заделки (защемления) можно получить два условия – равенство нулю прогиба и угла поворота в сечении заделки;

в) от каждой границы двух смежных участков полу­чаем два условия – равенство между собой прогибов и углов по­ворота общих сечений на границе обоих участков.

Начальными параметрами называются значения усилий и перемещений в сечении балки, принятом за начальное при отсчете абсцисс; другими словами, это значения ординат эпюр при z = 0 ( ).

Сущность этого метода покажем на примере балки постоянного сучения, находящейся под действием сосредоточенных сил P_1, P_2, … P_n на расстояниях а₁, а₂, ..., а_п от левого конца балки (рис.11).

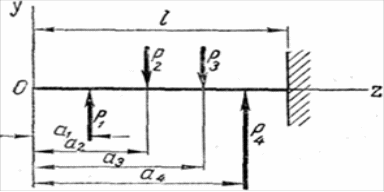
Рис. 11.

Напишем дифференциальные уравнения для участков балки.

Для 1-го участка (при а₁ ≤ z ≤ a₂ )

Для 2-го участка (при а₂≤ z ≤ a₃ )

Для 3-го участка (при а₃≤ z ≤ a₄ )

…………………………………………………………………

Для n-го участка (при а_n≤ z ≤ a_n+1 )

Проинтегрируем каждое из составленных дифференциальных урав­нений дважды, не раскрывая скобок. После первого инте­грирования получим:

…………………………………………………………………

В результате второго интегрирования получим:

…………………………………………………………………

При принятом способе интегрирования все постоянные каждого интегрирования получаются равными между собой, так как на любой границе, например при z = а₃, у обоих смежных участков изогнутой оси балки касательная и прогиб будут общими, т. е. у'₂ = у'₃ и у₂= у₃.

Подставив в соответствующие уравнения (второе и третье в каждой группе) значения z = a₃ и приравняв их правые части, получим С₂ = С₃ и D₂ = D₃, так как члены с множителем (z – а₃) обращаются в нуль. Таким образом, граничные условия представляются равенствами

и число постоянных интегрирования сведется только к двум, которые всегда могут быть определены исходя из условий закрепления балки.

Равенства постоянных интегрирования можно достигнуть и для случая загружения балки равномерно распределенной нагрузкой, даже если такая нагрузка претерпевает разрыв в некотором сечении, например при z = а₂ (рис. 12). Здесь равенство постоянных интегри­рования может быть достигнуто при применении искус­ственного приема, а именно: распределенную нагрузку продолжают до правого конца балки. Чтобы не изменить условия ее работы, к ней в этой же части прикладывают нагрузку, равную добавленной, но противоположную по направлению.

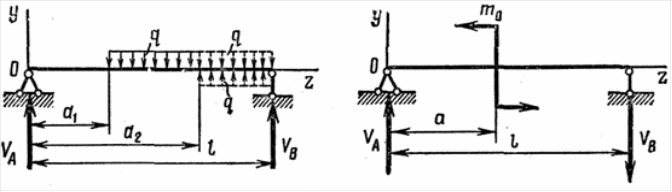
Рис. 12. Рис. 13.

При загружении балки сосредоточенной парой т₀ (рис. 13) обыч­ный способ составления выражения изгибающего момента на втором участке не приведет к равенству постоянных интегрирования. В этом случае дифференциальные уравнения будут иметь вид:

при .

при

Как видно, член, учитывающий во втором уравнении влияние т₀, не содержит множителя (z – а). Следовательно, после интегрирования он не обратится в нуль на границе участков, а это необходимо для получения равенства постоянных интегрирования.

В этом случае применяем искусственный прием: во второе уравнение вместо члена т₀ (при значении z > а) вводят равный ему член т₀ (z – а)⁰, поскольку (z – а)⁰ = 1. Благодаря этому приему равен­ство постоянных интегрирования будет обеспечено.

Выведем уравнение изогнутой оси балки в общем виде для слу­чаев простых загружении балок: сосредоточенными, равномерно рас­пределенными нагрузками и сосредоточенными парами сил.

При применении изложенных выше искусственных приемов отпадает необ­ходимость составлять и интегрировать дифференциальные уравнения для каждого участка балки; доста­точно ограничиться составлением и интегрированием только одного дифференциального уравнения для последнего (крайнего правого) участка и пользоваться этим урав­нением для других участков.

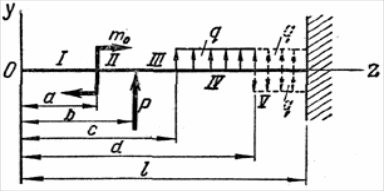
Рис. 14.

Пусть балка, изображенная на рис. 14, подвержена действию на­грузок т₀, Р и q. Составим диффе­ренциальное уравнение для последнего участка:

интегрируем его дважды:

Физический смысл постоянных интегрирования С и D может быть выяснен из рассмотрения упругой линии 1-го участка.

Ввиду отсутствия нагрузки на 1-м участке дифференциальное урав­нение упругой линии будет EJy" = 0. Интегрируя его дважды, получим

Обозначив тангенс угла наклона касательной к упругой линии и начале координат ₀. а прогиб в том же сечении f₀ при z = 0, получим

Следовательно, постоянная С выражает тангенс угла наклона каса­тельной в начале координат, умноженный на жесткость сечения балки EJ, а постоянная D – прогиб в начале координат, умноженный на ту же величину жесткости сечения балки.

Подставив значения постоянных интегрирования С и D для случаев многократного повторения рассмотренных видов нагрузок, получим:

уравнение углов поворота

уравнение прогибов

Полученные уравнения называются общими, или универсальными, уравнениями упругой линии балки.