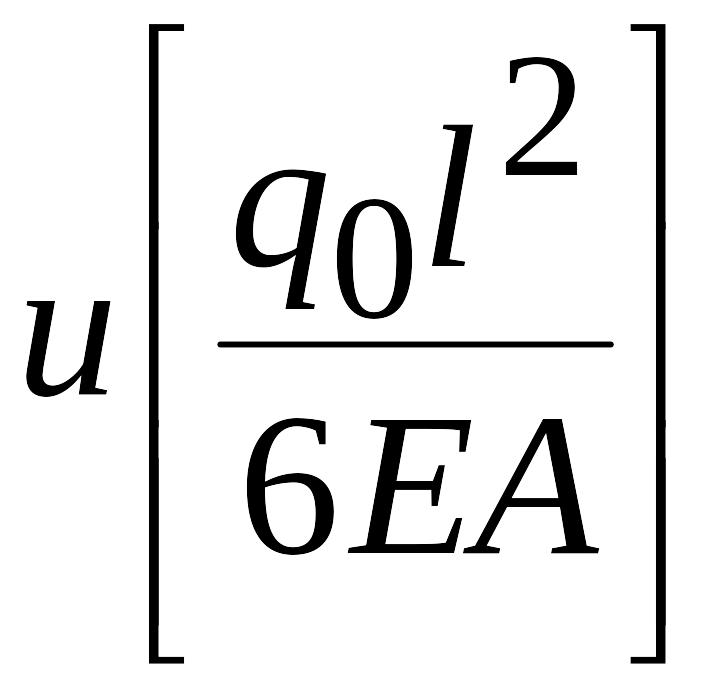- •Лекция 2
- •Точное решение
- •Лекция 3
- •Лекция 4
- •Лекция 5
- •2. Приближенные методы
- •2.1 Метод конечных разностей
- •Лекция 6
- •Лекция 7
- •Лекция 8
- •Лекция 9
- •2.2. Метод Бубнова-Галеркина
- •Лекция 10
- •Лекция 11
- •Лекция 12
- •2.3. Метод Ритца-Тимошенко
- •2.4. Метод наименьших квадратов
- •2.5. Метод коллокаций
- •2.6. Метод конечных элементов
- •Рекомендуемая литература Основная литература
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Факультет строительства и архитектуры
Кафедра строительных конструкций
В. Ф. Буравлев
Математическое моделирование
в строительстве
Курс лекций
Специальность:
290300 "Промышленное и гражданское строительство" (дневная форма обучения)
Киров 2005
Введение
Математическое моделирование – могучее средство изучения природы, техники и человеческого общества. Что такое модель? Слово «модель» в переводе с итальянского означает «копия, образец, прототип». Изучив модель, мы познаем оригинал. Значит, математическая модель – это прототип какой-то части мира – объекта, системы, устройства, машины, процесса, прибора, изучая который, мы постигаем эту часть мира. Мы будем рассматривать математические модели в относительно узкой области – механике упругого тела.
При расчете напряженно-деформированного состояния инженерных сооружений приходится иметь дело не с самим сооружением, а с его расчетной моделью. Физическая модель сооружения (расчетная схема) получается путем принятия некоторых упрощающих гипотез, не оказывающих заметного влияния на реальное поведение сооружения. Математическая модель описывает поведение физической модели с помощью определенных соотношений, связывающих между собой параметры, определяющие такое поведение. В качестве параметров могут выступать геометрические размеры, жесткостные характеристики, деформации, перемещения, усилия, напряжения и т. п. Например, для определения перемещений и усилий от собственного веса Останкинской телебашни (рис. 1а) можно использовать очень простую физическую модель – прямолинейный стержень, подвергающийся действию переменной распределенной нагрузки (см. рис. 2).
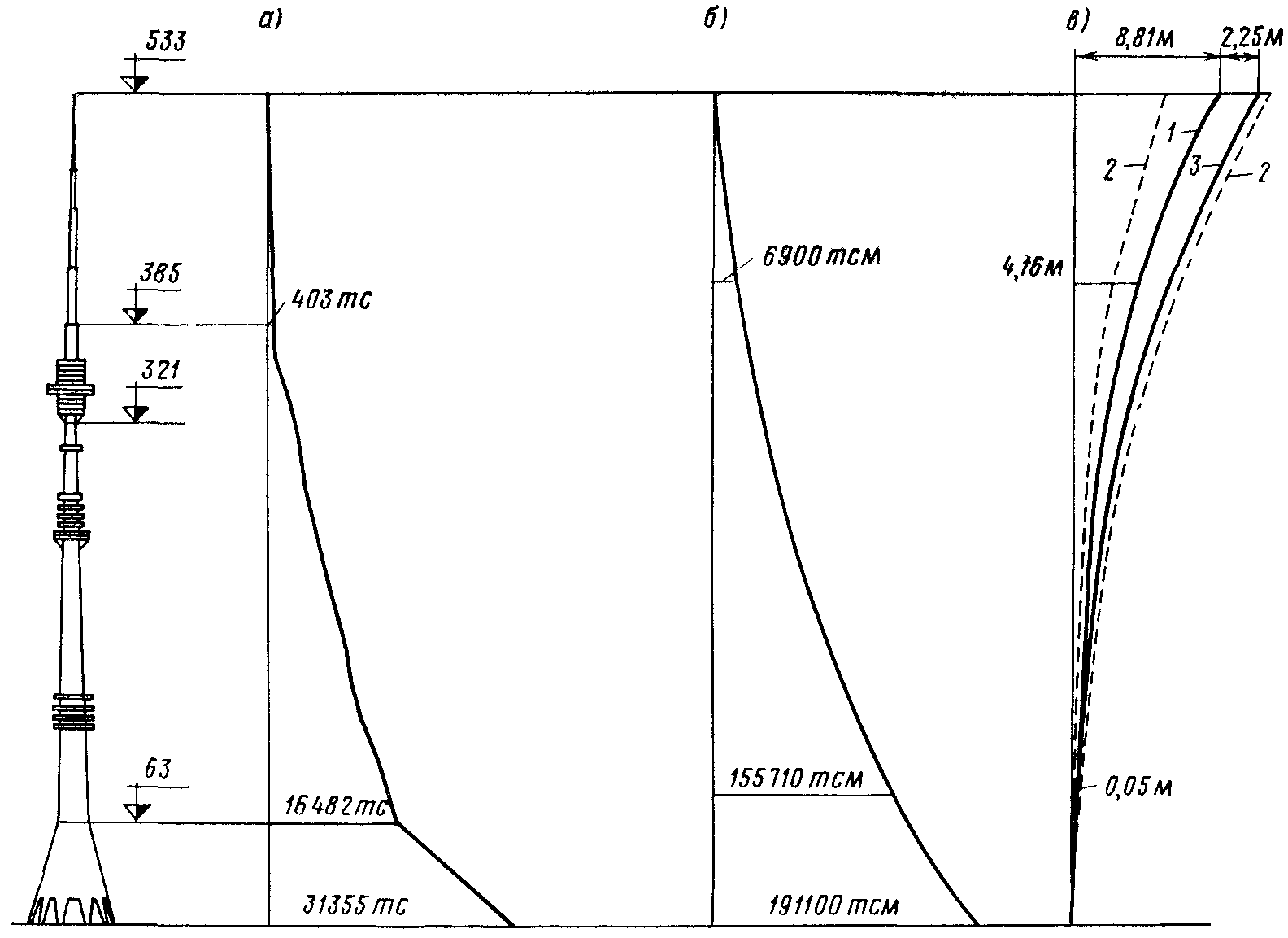
Рис. 1. Изменение продольных усилий от собственного веса (а), изгибающих моментов (б) и прогибов (в) от ветровой нагрузки по высоте Останкинской телебашни
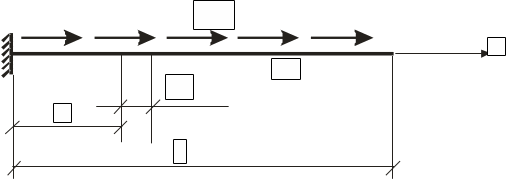
Рис. 2. Физическая модель (расчетная схема)
Математическая модель будет фигурировать в виде дифференциального уравнения
![]() ,
,
включающего перемещение u(x), распределенную переменную по координате x нагрузку q(x) и продольную жесткость ЕА(x) (Е – модуль упругости материала, А(x) – площадь сечения). При этом продольное усилие N(x) и перемещение u(x) связаны между собой соотношением
![]() .
.
Решение этой математической модели дает функцию перемещений и внутренних усилий, т. е. напряженно-деформированное состояние физической модели.
Лекция 1
Типы уравнений в механике твердого деформируемого тела
Рассмотрим построение математической модели для простейшего случая растяжения-сжатия стержня (рис. 2).
При решении задач механики твердого тела используются три типа уравнений:
1 – уравнения равновесия;
2 – деформационные соотношения;
3 – физические соотношения.
Эти уравнения получаются следующим образом.
1. Уравнения равновесия:
вырезается (мысленно) бесконечно малый элемент (у стержня – линейный длиной dx (рис. 3), у пластин и оболочек – плоский или искривленный прямоугольник c размерами dx, dy, у монолитных конструкций – параллелепипед со сторонами dx, dy, dz);
по местам разреза прикладываются неизвестные внутренние усилия и моменты (в нашем случае только продольные усилия N);
рассматриваются условия равновесия элемента.

Рис. 3. Бесконечно малый элемент стержня.
Запишем уравнение равновесия (сумму проекций на ось x)
![]() .
.
Деля на dx, получим:
![]() .
(1)
.
(1)
Таким образом, уравнения равновесия связывают между собой в дифференциальной форме внутренние силовые факторы и внешнюю нагрузку.
2. Деформационные соотношения получаются из рассмотрения деформированного состояния элемента.
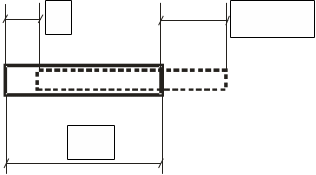
Рисунок 4. Деформация бесконечно малого элемента
Длина недеформированного элемента:
![]() .
.
Длина его после деформирования:
![]() .
.
Относительная (безразмерная) деформация:
![]() .
(2)
.
(2)
Таким образом, деформационные соотношения связывают между собой в дифференциальной форме деформации и перемещения
3. Интегрируя по площади закон Гука:
![]() ,
,
где
Е
– модуль упругости материала,
![]() -
напряжение, и учитывая, что в случае
растяжения-сжатия деформации в сечении
постоянны, приходим к соотношению:
-
напряжение, и учитывая, что в случае
растяжения-сжатия деформации в сечении
постоянны, приходим к соотношению:
![]() .
(3)
.
(3)
Таким образом, физические соотношения связывают между собой в алгебраической форме внутренние силовые факторы и деформации.
Внося в физические соотношения деформационные соотношения, получаем связь между внутренними силовыми факторами и перемещениями (соотношения Коши). В нашем случае
![]() .
(4)
.
(4)
Наконец, после внесения соотношений Коши в уравнения равновесия, приходим к уравнению упругого равновесия :
![]() ,
,
или, после деления на жесткость растяжения – сжатия EА:
![]() .
(5)
.
(5)
Это уравнение и предстоит решать различными способами.
Лекция 2
Точное решение
Уравнение (5) представляет собой дифференциальное уравнение второго порядка, решаемое в квадратурах, т. е. оно решается последовательным интегрированием. Проинтегрировав его дважды
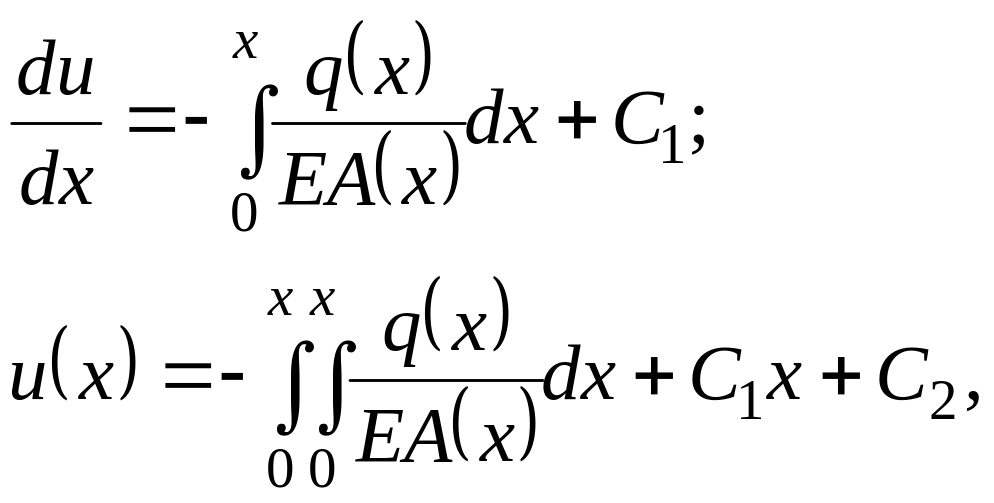 (1.1)
(1.1)
мы получим решение с точностью до констант интегрирования С1 и С2.
Эти константы определяются из граничных условий (из условий закрепления торцов стержня). Граничные условия могут быть геометрическими (ГГУ), когда на торцах заданы перемещения, статическими (СГУ), когда на торцах заданы силы, или смешанными, когда на одном торце заданы ГГУ, а на другом – СГУ.
Рассмотрим примеры решения при различных граничных условиях.
Пусть, например, нагрузка изменяется по линейному закону
![]() .
(1.2)
.
(1.2)
Дифференциальное уравнение (5) примет вид (ЕА=const):
![]() .
(1.3)
.
(1.3)
Дважды интегрируем уравнение (7):
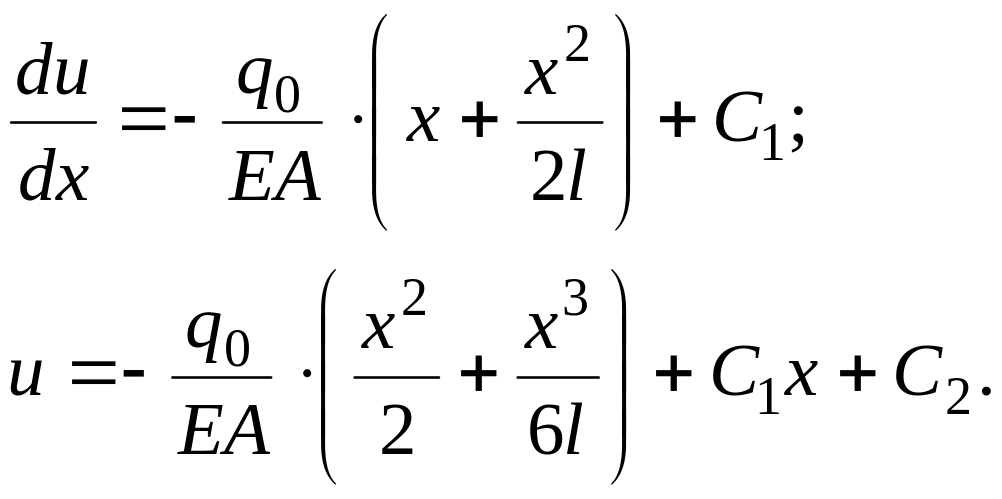 (1.4)
(1.4)
Рассмотрим геометрические ГУ (рис. 5 для варианта А).
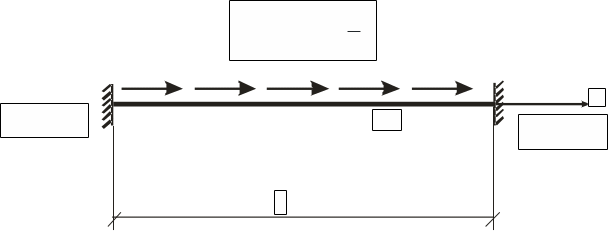
Рисунок 5. Геометрические граничные условия (вариант А)
Подчиним решение (9) геометрическим граничным условиям
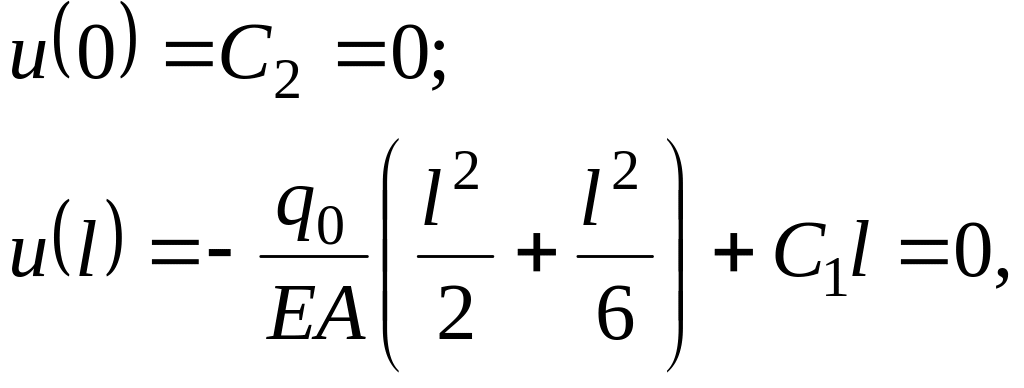 (1.5)
(1.5)
откуда
![]() (1.6)
(1.6)
Внося полученные значения констант во второе соотношение (1.4), получаем выражения для перемещения
![]() .
(1.7)
.
(1.7)
Здесь введена безразмерная координата
![]() .
(1.8)
.
(1.8)
На основании соотношения (4) получаем выражение для продольного усилия
![]() .
(1.9)
.
(1.9)
Произведем ручной счет по формулам (1.7) и (1.9) в пяти равноотстоящих точках. Результаты представим в виде таблицы 1 и графиков (рис. 6 и 7).
Таблица 1
|
0 |
0.25 |
0.5 |
0.75 |
1.0 |
|
0 |
51/64 (0.797) |
9/8 (1.125) |
57/64 (0.891) |
0 |
|
4.0 |
37/64 (2.313) |
1/4 (0.25) |
-35/16 (-2.188) |
-5 |

Рис 6. Изменение продольного перемещения по длине стержня (точное решение - вариант А)

Рис. 7. Изменение продольного усилия по длине стержня (точное решение - вариант А)
Запишем программу, численно реализующую выражения (1.7), (1.9), на алгоритмическом языке «Паскаль».
PROGRAM STTR;
uses crt;
const
qo=1.0; l=1.0; EA=1.0; m=4;
var i: integer;
qoln,qolu,dx,x,x3: real;
u,N: array[1..m+1] of real;
BEGIN
clrscr;
qoln:=qo*l/6;
qolu:=qoln*l/EA;
dx:=l/m;
writeln;
writeln(‘ Результат решения’);
writeln;
writeln(‘Координата Перемещение Усилие’);
for i:=1 to m+1 do begin
x:=dx*(i-1)/l;
x2:=sqr(x);
u[i]:={qolu*}x*(-x2-3*x+4);
N[i]:={qoln*}(-3*x2);
writeln;
writeln(‘ x=’,x:5:3,
‘ u=’,u[i]*6:7:4,’ N=’,N[i]*6:7:4);
end;
readln;
END.