Контрольные вопросы к разделу 9

1. Постройте функцию Уолша wol₁₀(q). Функцию wol₁₆(q).

2. Вычислите 8 коэффициентов ряда Фурье для функции wol₄(q).

3. Представьте функцию рядом по функциям Уолша.

10. Вейвлет–преобразование сигналов

10.1. Описательная характеристика вейвлетов

В последние годы в теории и технике обработки сигналов различной природы начали успешно применяться вейвлет-преобразования.

Теория и практика вейвлетов, сформировавшиеся как самостоятельные направления в 90-ые годы ХХ века, находятся в самом начале процесса своего бурного развития и поэтому еще не сложилось окончательное представление об их подлинных возможностях. Но уже сейчас ясно, что вейвлет-преобразования пригодны и удобны для обработки и исследования изображений, нестационарных сигналов, неоднородных полей, для распознавания образов и высокоточного представления импульсных и цифровых сигналов, т.е. для решения именно тех задач, которые были и продолжают оставаться наиболее проблемными при использовании традиционных преобразований.

Термин "вейвлет" был введен в середине 80-ых годов ХХ века в связи с анализом сейсмических и акустических сигналов. Практически сразу же вслед за этим началось исследование вейвлетов методами математики. С английского слово wavelet переводится как "короткая (маленькая) волна". В названии отражен основной признак вейвлета – ограниченность его существования во времени (протяженности в пространстве). Именно это свойство дает основание рассматривать вейвлеты в качестве нового удобного базиса представления произвольных сигналов, прежде всего сигналов импульсных, отличных от нуля на ограниченных, сравнительно коротких интервалах значений своего аргумента.

По сути дела, низкая эффективность представления рядами Фурье функций и сигналов с резко выраженными локальными особенностями связана именно с бесконечной протяженностью во времени (в пространстве) гармонических колебаний – базисных функций разложения Фурье. Практика работы с рядами Фурье вынуждает прибегать к усечению бесконечного числа членов ряда некоторым их конечным числом. Однако простое усечение ряда приводит к нежелательному эффекту, называемому явлением Гиббса. Этот эффект проявляется в виде пульсаций с выбросами в области точек разрыва аппроксимируемой функции. При такой аппроксимации максимальный выброс пульсаций в особой точке аппроксимируемой функции может оказаться соизмеримым с величиной перепада (скачка) функции, аппроксимируемой усеченным рядом. Причем скачок этот не убывает с увеличением числа учитываемых членов ряда Фурье. По мере увеличенияуменьшается только ширина выброса. Поэтому на практике усечение ряда производят не путем резкого отбрасывания членов ряда, а с помощью весовых последовательностей конечной длины, называемых окнами. Известно много вариантов окон, например, прямоугольное окно, окно Хэмминга, окно Кайзера, окно Дольфа-Чебышева и др. При этом задача выбора хорошего окна фактически сводится к отысканию такой ограниченной во времени функции, преобразование Фурье которой наилучшим образом аппроксимирует заданную функцию, ограниченную по частоте. Наилучшей считается такая аппроксимирующая весовая функция (окно), спектр которой имеет минимальную энергию за пределами заданного интервала частот. Задача выбора окна зачастую оказывается сложной. По мнению автора одного из окон – Хэмминга: "весовые функции представляют собой наиболее «запутанную» часть во всей теории цифровых фильтров".

Кроме того, при анализе и обработке почти всегда очень важно знать не только частотный состав сигнала, но и его расположение на оси времени (а для пространственно-временных сигналов еще и в пространственных координатах). Тут наблюдается полная аналогия с описаниями сигнала посредствам нотной грамоты: нота сообщает исполнителю не только высоту тона музыкального звука, но также и момент его создания и продолжительность во времени. В теории и технике сигналов таким удобным аппаратом для единого пространственного, временного и частотного представления процессов оказались вейвлеты.

Вейвлеты – это обобщенное название особых функций, имеющих вид достаточно коротких волновых пакетов, т.е. локализованных на некотором отрезке оси независимой переменной (времени или пространства). Конкретный волновой пакет (вейвлет) имеет свою определенную, подчас сложную форму, может сдвигаться заданным образом по оси независимой переменной и одновременно подвергаться сжатию – растяжению (масштабированию). Масштабированием задается размер «окна», а сдвигом – его положение на оси независимой переменной. При этом интегральное значение волнового пакета равно нулю.

Приведенное вербальное, описательное определение вейвлетов указывает на большое разнообразие их типов. Это разнообразие расширяет круг задач, решаемых с помощью вейвлетов, но сами решения прикладных задач потребуют творческого подхода к выбору того или иного конкретного типа вейвлет-преобразования.

Функции, образующие ортонормированный базис вейвлет-преобразования, удовлетворяют условию

.

Как следует из , все базисные функции получаются из исходного базисного вейвлета – его еще называют материнским вейвлетом – путем выполнения операций сдвига по аргументу (во времени и/или в пространстве), определяемого параметром, и изменения масштаба (временного и/или пространственного сжатия – растяжения), задаваемого параметром. Множительобеспечивает независимость нормы

от масштабирующего параметра .

Один из материнских вейвлетов и суть образования от него семейства вейвлетов путем масштабирования и временного сдвига показаны на рис. 10.1.

Рис. 10.1. Образование базисных функций вейвлет-преобразования

В теории вейвлетов наиболее часто используется бесконечно-размерное гильбертово пространство. А в этом пространстве – только те функции , которые удовлетворяют условиям:

;

.

Поэтому вейвлет-функции в таком пространстве принципиально должны иметь нулевое среднее значение и затухать на бесконечности, т.е. быть «короткими волнами».

Поскольку интервал существования (действия) вейвлетов ограничен, они способны покрыть всю вещественную ось независимой переменной или ее заданную часть только в том случае, если имеют возможность сдвига по этой оси. Для обеспечения высокой детализации при преобразовании должна быть предусмотрена возможность масштабирования (сжатия/растяжения) вейвлетов. Масштабирование играет ту же роль, что и изменение частоты гармоник в рядах Фурье. Но в то время, как в рядах Фурье протяженность гармоники (при любой частоте) бесконечна, масштабирование изменяет протяженность вейвлета. Это видно на рис. 10.1. Указанное свойство вейвлетов обеспечивает их главное преимущество перед синусоидами – способность представлять локальные особенности функций и сигналов.

Вейвлеты характеризуются не только своим временны́м, но и частотным образами. Временно́́й образ определяется приведенной выше пси-функцией времени в виде формулы . Частотный образ вейвлета определяется Фурье-образом его пси-функции, который задает огибающую спектра вейвлета посредством известного выражения

.

В качестве примера на рис. 10.2 показаны временно́́й а) и частотный б) образы вейвлета, известного под названием «мексиканская шляпа». Это один из немногих вейвлетов, временно́́й образ которого задается аналитическим выражением, а именно – второй производной от функции Гаусса (квадратичной экспоненты)

где – обозначение вейвлета «мексиканская шляпа».

Рис. 10.2. Вейвльвет "мексиканская шляпа"

На рис. 10.2 видно, что данный вейвлет похож на затухающую синусоиду с интегральной площадью, равной нулю (или очень близкой к нулю). Заметим, что точное равенство нулю площади функции (под и над осью времени, с учетом знака) является одним из непременных условий, позволяющих отнести функцию к вейвлетам. Характер колебаний рассматриваемого вейвлета позволяет говорить о некоторой «средней частоте» колебаний. При этом сужение вейвлета во времени (в пространстве) сопровождается повышением «средней частоты» , перемещением спектра вейвлета в область более высоких частот с одновременным его расширением.

Материнский вейвлет характеризуется параметрами ; полученные на его основе вейвлетные функции характеризуется параметрами(узкий) и(широкий), т.е. образованы только за счет масштабирования без сдвига во времени. При изменении параметраот 0,5 до 2 спектр смещается в область более низких частот, его ширина уменьшается, а амплитуда увеличивается. Так «высвечиваются» (подчеркиваются) разные участки спектра обрабатываемого сигнала.

Описанный процесс протекает так: если вейвлет сужается вдвое, то его «средняя частота» и ширина спектра возрастают вдвое. Одновременное изменение «средней частоты» (местоположения частотного центра) и ширины полосы спектра обратно пропорционально изменению масштабного параметра характерно для всех вейвлетов. Как показано в, следствием этого является то, что отношение

у вейвлет-функций не зависит от параметра .

По рис. 10.2 также видно, что одинаково хорошая локализация вейвлетов одновременно во временнoй и частотной областях невозможна. Однако следствие из данного факта совсем иное, чем в случае оконного преобразования Фурье. Здесь более высокая временнaя локализация вейвлета сопровождается не только расширением его спектра, но и смещением всех значащих спектральных составляющих в область более высоких частот. Последнее как раз и обеспечивает наилучшие условия для представления кратковременных локальных особенностей сигналов. При оконном преобразовании Фурье сужение окна приводит лишь к «размазыванию» энергии в более широкой полосе спектра; никакого «подчеркивания» высокочастотных составляющих здесь не происходит.

На рис. 10.3, а) и в) показан вид вейвлета Хаара во временнoй области и вид его преобразования Фурье в частотной области. Этот вейвлет является наиболее простым среди вейвлетов. Он представляет собой следующую ступенчатую функцию

Рис. 10.3. Вейвлет Хаара

Область определения – интервал, но и он претерпевает разрывы в точкахи. Преобразование Фурьевейвлетадает следующий результат

Фурье-образ рис. 10.3,б и г достаточно хорошо локализован на частоте , но медленно убывает при увеличении частоты, что является следствием разрывности(рис. 10.3,а). Точка локализации спектра при сместилась в область более низких частот (рис. 10.3,г). Модуль имеет максимум на частотеи убывает какпри.

Описанная связь временны́́х и частотных свойств вейвлетов позволяет в процессе вейвлет-преобразований по меньшей мере решать две задачи.

1. Обеспечить выявление тонких особенностей сигналов или изображений; при этом реконструкции (восстановления) их не требуется. В таком случае подбираются типы вейвлетов, которые хорошо согласуются с особенностями обрабатываемого сигнала или изображения, причем вейвлеты не обязательно должны быть ортогональными.

3. Обеспечить в процессе прямого вейвлет-преобразования сигнала (изображения) получение вейвлет-спектрограммы, несущей информацию о локальных особенностях сигнала (изображения), а затем по запомненной спектрограмме в процессе ее обратного вейвлет-преобразования реконструировать сигнал (изображение) с заданной точностью и в нужное время. Полная реконструкция сигнала возможна только при использовании ортогональных вейвлетов.

Практическое применение вейвлетов начинается с выбора в качестве базисной короткой волны (анализирующего вейвлета) вполне определенного типа. Эта волна должна порождать соответствующее семейство (систему) базисных функций-вейвлетов, способных обеспечить через свое посредство заданную форму и точность представления обрабатываемого сигнала или преобразуемой функции.

Короткая волна, удовлетворяющая требованиям к вейвлетам, может быть выбрана среди функций разного вида, но в каждом конкретном вейвлет-преобразовании должна быть задействована волна только одного вида. Эту волну – анализирующий вейвлет принято называть материнским вейвлетом . На рис. 10.1 изображена материнская функция, областью определения (компактным носителем) которой является отрезок– верхний рисунок.

Материнский вейвлет порождает целый пакет вейвлетных функций, общее выражение для которых задается соотношением . Функциисоздаются на основе функциив результате выполнения двух операций:

– смещения по оси времени (или по пространственной оси), обозначаемого какпри;

– масштабирования, обозначаемого как при.

Параметр задает ширину вейвлетной функции, а– ее положение на соответствующей оси. Чтобы это учесть, иногда используют обозначения

Вейвлет-функции обеспечивают определение деталей сигнала и нахождение детализирующих коэффициентов. Эти функции колеблются относительно оси(или оси). Частота их колебаний зависит от значения масштабирующего параметра: малым значениямсоответствуют высокие частоты, а большим – низкие частоты. Или более определенно:

– значения соответствуют очень узким окнам и выбираются для точно локализованной регистрации особенностей сигнала по характеристикам спектра в области высоких частот;

– значения соответствуют очень широким окнам и служат для регистрации медленных процессов или длинноволновых колебательных составляющих сигнала по характеристикам низких частот.

Изменение коэффициента масштабирования приводит к изменению ширины и амплитуды вейвлета: привейвлет уже вейвлетов прии, но его амплитуда больше, чем у них. Такие изменения параметров вейвлета не зависят от конкретного значения сдвига. Сдвиг лишь определяет положение вейвлета на оси времени. Это наглядно показано на рис. 10.2.

Однако, вейвлет-преобразования на основе одних только детализирующих вейвлет-функций , даже если они ортогональные, не всегда способны восстановить сигнал в целом. Они способны реконструировать тонкие детали временнoй зависимости. Но для восстановления полной формы сигнала необходима еще одна временна́́я функция, называемая аппроксимирующей. Другое ее название – отцовский вейвлет.

Площадь этой функции равна единице, т.е.

.

Она обеспечивает грубое приближение (аппроксимацию) сигнала и нахождение коэффициентов аппроксимации. Не все вейвлеты имеют в своем арсенале функцию . Ее имеют только ортогональные вейвлеты. Простейшим примером такого вейвлета является функция Хаара.

Из определения вейвлета следует, что на протяжении своего существования он не осциллирует. Функция , материнский вейвлети первые несколько вейвлет-функций Хаара изображены на рис. 10.4.

Рис. 10.4. Первые несколько вейвлет – функций Хаара

Этот рисунок наглядно показывает основную разницу между отцовскими вейвлетами и материнскими вейвлетами. Строго говоря, отцовский вейвлет не удовлетворяет основному требованию к вейвлетам: его площадь не равна нулю. Но без него невозможна реконструкция сигнала по вейвлет-спектрограмме. На рисунке наглядно видно, как при изменении значений параметров ипроисходит сжатие/растяжение и сдвиг вейвлета.

Матрица восьми дискретных значений функции Хаара имеет следующий вид:

Каждая строка матрицы соответствует своей строке рис. 10.4: отцовскому вейвлету (первая строка), материнскому вейвлету (вторая строка), вейвлету - третья строка, вейвлету– четвертая строка, вейвлетам,,,- пятая, шестая, седьмая и восьмая строки соответственно. Такая матрица может храниться в вычислителе, осуществляющем вейвлет-преобразование.

В качестве базисных (материнских) часто применяются вейвлеты гауссовой формы, цилиндрической формы и др. На рис. 10.5 изображены гауссовы вейвлеты первых четырех порядков и модули их спектральной плотности. В таблице 10.1 приведены выражения для гауссовых и других вейвлетообразующих функций.

Рис. 10.5. Гауссовы вейвлеты первых четырех порядков (1 – wave, 2 – mhat и т.д.) а и модули их спектрадльных плотностей (преобразования Фурье от вейвлетов) б

Таблица 10.1

Вид вейвлета	Аналитическая запись	Спектральная плотность
Вещественные непрерывные базисы
Гауссов первого порядка (или WAVE-вейвлет)
Гауссов второго порядка (или MHAT-вейвлет «мексиканская шляпа»)
Гауссов -го порядка
DOG-вейвлет
LP-вейвлет
Вещественные дискретные базисы
HAAR-вейвлет
FHAT-вейвлет (или «французская шляпа» – похож на цилиндр)
Комплексные базисы
Морле-вейвлет
Пауля-вейвлет (чем больше, тем больше нулевых моментов имеет вейвлет)		Примечание:

Поскольку для осуществления вейвлет-преобразования требуются вейвлеты с разным затуханием, возникает необходимость сжатия/растяжения материнского вейвлета. Свойство затухания вейвлета, в свою очередь, порождает проблему покрытия им всей вещественной оси (оси времени, пространственной оси). Сжатие, как уже говорилось, обеспечивает получение коротких волн нужных частот. Проблема покрытия разрешается введением операции сдвига функциивдоль соответствующей оси. Но имеется также проблема практической реализации, связанная с объемом вычислений.

Суть в следующем. Невозможно в обозримое время произвести вычисления для бесконечно большого числа точек вещественной оси, в которые следовало бы осуществить сдвиг предельно короткого вейвлета с целью обеспечения наивысшей точности представления сигнала, функции, изображения и т.п. Приемлемы только сдвиги в конечное число точек области существования сигнала, функции и т.д.

Из соображений практической реализуемости в расчетах должно использоваться также конечное число значений параметра .

Реальное сокращение вычислительных затрат при выполнении вейвлет-преобразования достигается в случае использования диадной (двоичной) дискретизации значений и, являющихся параметрами сжатия/растяжения и сдвига соответственно. При такой дискретизации значенияизадаются на множестве целых чиселв видеи, гдеи- целые числа;- параметр масштаба.

Конечно, возможны и иные способы задания дискретных значений и. Например, простейший способ сдвига – последовательность всех целочисленных сдвигов, т.е., где.

Однако вычислительная избыточность вейвлет-преобразований исключается лишь при использовании диадной (двоичной) сетки дискретизации. Это связано с тем, что при такой дискретизации не происходит перекрытия носителей (областей определения) вейвлетов, а, значит, устраняется необходимость двойных вычислений в областях перекрытия. Иначе говоря, в случае диадного преобразования компактные носители вейвлетов плотно укладываются на оси (на оси) не перекрываясь, а сами вейвлеты могут быть представлены в виде.

Диадная дискретизация параметров инапрямую не связана с использованием двоичного кода в цифровом процессоре, реализующем вейвлет-преобразование. Ясно, что на практике и непрерывное вейвлет-преобразование производится в том или ином дискретном варианте. Хотя при этом особых ограничений на характер дискретизации параметровине накладывается, предпочтительнее диадная дискретизация. Что касается необходимой при цифровой обработке дискретизации самих вейвлет-функций, то она должна проводится в соответствии с известной теоремой отсчетов.

Для реализации рекомендаций теоремы отсчетов надо знать не только временные параметры вейвлета, но и его частотные свойства. Как указывалось выше, вейвлеты имеют свое частотное представление в виде Фурье-образа . На рис. 10.3, б и 10.3, г видно, что , а спектр (Фурье-образ) напоминает всплеск, пик которого приходится на «среднюю» круговую частоту вейвлета. Как уже указывалось, имеется прямая связь между временны́́м и частотным представлением вейвлетов: малые значения параметрахарактеризуют быстрые изменения в сигналах и соответствуют высоким частотам, а большие его значения характеризуют медленные изменения сигнала и соответствуют низким частотам.

Частотное представление вейвлетов позволяет оценить фильтрующие свойства вейвлет-преобразований, которые лежат в основе алгоритма быстрого вейвлет-преобразования.

При использовании диадной дискретизации в вейвлет-преобразованиях предпочтение отдается волнам с частотами, разделенными на последовательные «октавы» (частотные диапазоны). При этом наибольшая вычислительная эффективность достигается при использовании для частотного разбиения целых степеней числа 2, т.е. при использовании множества малых волн вида

где .

Обратившись к выражению можно обнаружить, что получено из одной «вейвлет-функции» в результате двоичного растяжения враз и двухпараметрического сдвига на. Действительно, записав в виде, сразу обнаруживается, чтои, откуда и следуют значения растяженияи временного сдвига. Дискретизированная таким образом функция принимает вид,.

Для любых норма функции (3.98) равна

.

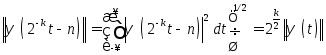В качестве исходного вейвлета выбирается такая функция, чтобы образованное на ее основе семейство базисных функцийявлялось ортонормированным, т.е., чтобы выполнялись соотношения

Только с использованием такого семейства сигналможет быть представлен вейвлет-рядом

,

в котором вейвлет-коэффициенты определяются соотношением

.

В теории вейвлетов определено также интегральное (непрерывное) вейвлет-преобразование. Применительно к функциям (сигналам) , заданным на вещественной оси и удовлетворяющим неравенству , оно записывается в виде

,

где – означает, что оператор интегрального вейвлет-преобразования (при известном базисном вейвлете)действует на преобразуемый сигнал, когда вейвлет имеет сдвиги масштаб, определяемый значением.

При использовании диадной сетки дискретизации параметров ипреобразование позволяет определить коэффициенты ряда по соотношению

т.е. при подстановке в правую часть значений и.

Следовательно, -й вейвлет – коэффициент (-ая составляющая вейвлет-спектра) функцииопределяется интегральным вейвлет-преобразованием ее, вычисленным с использованием вейвлета, характеризуемого сдвигоми двоичным растяжением. Таким образом, в одной и той же точке сдвига тот же самый ортонормированный вейвлетиспользуется и для формирования ряда и для получения интегрального вейвлет-преобразования . Это указывает на тесную связь вейвлет-ряда и интегрального преобразования сигнала при использовании вейвлета одного и того же вида.

Согласно формуле в процессе интегрального вейвлет-преобразования обеспечивается возможность формирования гибкого частотно-временно́́го окна путем задания последовательности значений иизменением. В результате окно будет автоматически выделять высокочастотные центры сигнала (разрывы и т.п.), когда окно узкое, и области медленных изменений сигнала (низкочастотные участки), когда окно широкое.

По известному вейвлет-преобразованию может быть восстановлен любой сигнал конечной энергии. Формула для восстановления сигнала имеет вид:

,

где , а константаравная;– преобразование Фурье вейвлета.

Для ортонормированных вейвлетов . Формула описывает обратное непрерывное вейвлет-преобразование. То есть опять имеем аналогию с Фурье-преобразованиями. Соотношение указывает на то, что вейвлет-спектр сигналаявляется функцией двух аргументови. Такой спектр существенно информативнее Фурье-спектра того же сигнала, зависящего только от одного аргумента. Более высокая информативность определяется тем, что вейвлет-спектр содержит сведения одновременно и об интенсивности частотных составляющих и о моментах времени, в которые так или иначе проявляются частотные составляющие сигнала.

Аргумент – это аргумент временного масштаба; он аналогичен периоду осцилляций, поскольку обратен частоте, т.е. опосредованно он определяет частотную ось. Аргумент– аргумент смещения сигнала по оси времени, т.е. является чисто временны́́м аргументом.

Если зафиксировать значение , тобудет описывать временную зависимость вейвлет-спектра сигнала при временном масштабе, т.е. описывать огибающую спектра в плоскости, перпендикулярной плоскости, как функцию сдвига(или, что почти одно и то же – времени).

Если положить , то огибающая вейвлет-спектрабудет показывать его частотную зависимость при фиксированном смещении по оси времени, равном. Характер этой зависимости указывает на наличие (или на отсутствие) особенностей у сигнала в момент. В частности, для сигнала в виде одиночного импульса длительности, сосредоточенного в окрестности, вейвлет-спектр имеет максимальное значение в точке с координатами ().

В связи с изложенным, вейвлет-спектр сигналаизображается поверхностью в трехмерном пространстве (плоскость, амплитуда), как это условно показано на рис. 10.5, а. Так как переменная описывает сдвиг по временно́́й оси, то в теории вейвлетов принято– ось располагать горизонтально, а-ось вертикально, как это изображено на рис. 10.5,а.

Рис. 10.5. Вейвлет-спектр в трехмерном пространстве

На рис. 10.6, а оси параметров илежат в горизонтальной плоскости так, что при наблюдении сверху по оси амплитуд поворот от осик осидо их совмещения должен происходить против часовой стрелки.

Изображать трехмерную поверхность сложно, и поэтому на практике ограничиваются представлением ее проекции на плоскость в виде изоуровней (рис. 10.5,б). Изоуровни позволяют оценить изменение значений вейвлет-преобразования на разных масштабах и сдвигах во времени. Они же позволяют выявить наличие возможных локальных экстремумов, расположение и уровни которых несут информацию о структуре анализируемого сигнала.

Таким образом, вейвлет-преобразования обеспечивают внешне сходные с Фурье-преобразованиями процедуры разложения и восстановления сигналов. Но вейвлет-преобразования позволяют сделать это на более высоком качественном и информационном уровне. Это связано с двумерностью вейвлет-спектра, получаемого при разложении сигнала и с восстановлением его по такому спектру.