
- •Часть 2. Радиосигналы и радиопомехи
- •4. Электрические сигналы
- •Контрольные вопросы к разделу 4
- •5. Аналитические модели сигналов
- •Упражнения к разделу 5
- •Контрольные вопросы к разделу 5
- •6. Векторные модели сигналов
- •Упражнения к разделу 6
- •Контрольные вопросы к разделу 6
- •7. Спектральные модели сигналов.
- •7.1. Представление сигналов рядами Фурье
- •7.1.1. Примеры спектров периодических сигналов
- •7.1.2. Частотные спектры непериодических сигналов
- •7.1.3. Свойства преобразование Фурье
- •8. Представление сигналов рядом Котельникова
- •Контрольные вопросы к разделу 8
- •9. Представление сигналов функциями Уолша
- •Контрольные вопросы к разделу 9
- •10. Вейвлет–преобразование сигналов
- •10.1. Описательная характеристика вейвлетов
- •10.2. Основные свойства вейвлет-анализа
- •10.3. О цифровой обработке сигналов на основе вейвлетов
- •Контрольные вопросы к разделу 10
7.1.3. Свойства преобразование Фурье
Разложение
сигнала
![]() в ряд по тригонометрическим функциям
базируется на основных свойствах
преобразования Фурье. Кратко эти свойства
сводятся к следующим.
в ряд по тригонометрическим функциям
базируется на основных свойствах
преобразования Фурье. Кратко эти свойства
сводятся к следующим.
1.
Сложение сигналов. Преобразование
Фурье, определяющее спектральную
плотность сигнала, является линейным.
Поэтому при сложении сигналов
![]() ,
,![]() ,…, имеющих спектры
,…, имеющих спектры![]() ,
,![]() …,
суммарному сигналу
…,
суммарному сигналу![]() будет соответствовать спектр
будет соответствовать спектр![]() .
.
2.
Сдвиг сигналов во времени.
Сигнал
![]() произвольной формы, существующий на
интервале времени отt1
до t2
и имеющий спектральную плотность
произвольной формы, существующий на
интервале времени отt1
до t2
и имеющий спектральную плотность
![]() ,
путем задержки его на времяt0
без изменения формы превращается в
сигнал
,
путем задержки его на времяt0
без изменения формы превращается в
сигнал
![]() ,
существующий на интервале от
,
существующий на интервале от![]() до
до![]() ,
без каких-либо видимых изменений формы
по сравнению с
,
без каких-либо видимых изменений формы
по сравнению с![]() .
Однако сдвиг (смещение) во времени
сигнала
.
Однако сдвиг (смещение) во времени
сигнала![]() на величину
на величину![]() вызывает изменение фазовой характеристики
спектра
вызывает изменение фазовой характеристики
спектра![]() на величину
на величину![]() .
Таким образом, спектр задержанного
сигнала можно записать в виде
.
Таким образом, спектр задержанного
сигнала можно записать в виде
![]() .
.
Верно
и обратное: если всем составляющим
спектра сигнала
![]() дать соответствующий их частотам фазовый
сдвиг
дать соответствующий их частотам фазовый
сдвиг![]() ,
линейно связанный с частотой
,
линейно связанный с частотой![]() ,
то сигнал претерпит сдвиг во времени
на
,
то сигнал претерпит сдвиг во времени
на![]() .
При этом амплитудно-частотная
характеристика сигнала (модуль
спектральной плотности) от положения
сигнала на оси времени не зависит.
.
При этом амплитудно-частотная
характеристика сигнала (модуль
спектральной плотности) от положения
сигнала на оси времени не зависит.
3.
Смещение спектра сигнала.
Разделение спектральной плотности
![]() сигнала
сигнала![]() на две части, смещенные соответственно
на
на две части, смещенные соответственно
на![]() и
и![]() ,
обеспечивается умножением сигнала
,
обеспечивается умножением сигнала![]() на гармоническое колебание
на гармоническое колебание![]() :
:
![]()
4.
Произведение двух сигналов.
Если сигнал
![]() представляет собой произведение двух
сигналов
представляет собой произведение двух
сигналов![]() и
и![]() ,
причем спектры этих трех сигналов
описываются функциями
,
причем спектры этих трех сигналов
описываются функциями![]() ,
,![]() и
и![]() соответственно, то спектр произведения
двух сигналов
соответственно, то спектр произведения
двух сигналов![]() и
и![]() равен свертке их спектров
равен свертке их спектров![]() и
и![]() ,
взятой с коэффициентом
,
взятой с коэффициентом![]() ,
т.е.
,
т.е.
![]() .
.
Аналогично,
произведению двух спектров
![]() соответствует результирующий сигнал
соответствует результирующий сигнал![]() ,
являющийся сверткой сигналов
,
являющийся сверткой сигналов![]() и
и![]() :
:
![]() .
.
А так как
![]() ,
,
то
![]() и
и![]() можно рассматривать соответственно
как входной сигнал
можно рассматривать соответственно
как входной сигнал![]() и импульсную характеристику
и импульсную характеристику![]() линейной части прибора, обрабатывающего
сигнал
линейной части прибора, обрабатывающего
сигнал![]() ,
а
,
а![]() и
и![]() – как спектральную плотность сигнала
– как спектральную плотность сигнала![]() и передаточную характеристику
и передаточную характеристику![]() линейной части прибора.
линейной части прибора.
Полезным может оказаться также соотношение между произведениями сигналов и их спектров, записанное в виде:
![]() ,
,
где
![]() -
спектральная функция, комплексно –
сопряженная функции
-
спектральная функция, комплексно –
сопряженная функции![]() .
.
Соотношения (3.33) и (3.36) часто используются при реализации процедур цифровой обработки сигналов. Благодаря применению алгоритмов БПФ они позволяют реализовать высокоскоростную обработку способом "быстрой свертки".
5.
Свойство
двойственности. Если
![]() есть преобразование Фурье функции
есть преобразование Фурье функции![]() ,
то преобразование Фурье сигнала
,
то преобразование Фурье сигнала![]() ,
полученному в результате заменыw
на t,
равно
,
полученному в результате заменыw
на t,
равно
![]() .
Иначе говоря, переменныеt
и –w
взаимозаменяемы, ч учетом масштабного
множителя 2p.
.
Иначе говоря, переменныеt
и –w
взаимозаменяемы, ч учетом масштабного
множителя 2p.
6.
Изменение
масштаба времени.
Пусть сигнал
![]() подвергся сжатию во времени в
подвергся сжатию во времени в![]() раз.
В результате получен сигнал
раз.
В результате получен сигнал![]() .
Спектральная плотность сжатого сигнала
связана со спектральной плотностью
исходного сигнала соотношением:
.
Спектральная плотность сжатого сигнала
связана со спектральной плотностью
исходного сигнала соотношением:
![]() .
.
Таким
образом, при сжатии сигнала в
![]() раз на временнoй оси во столько же раз
расширяется его спектр на оси частот.
Модуль спектральной плотности при этом
уменьшается в
раз на временнoй оси во столько же раз
расширяется его спектр на оси частот.
Модуль спектральной плотности при этом
уменьшается в![]() раз. Соответственно, при растягивании
сигнала во времени, т.е. при
раз. Соответственно, при растягивании
сигнала во времени, т.е. при![]() ,
имеют место сужение спектра и увеличение
модуля спектральной плотности.
,
имеют место сужение спектра и увеличение
модуля спектральной плотности.
7.
Дифференцирование и интегрирование
сигнала.
Если сигнал
![]() имеет
спектр
имеет
спектр![]() ,
то спектральная плотность его производной
,
то спектральная плотность его производной![]() будет
будет![]() .
Спектральная плотность интеграла
.
Спектральная плотность интеграла![]() составит
составит![]() .
.
8.
Для
смещения спектра
![]() исходного сигнала
исходного сигнала![]() на
на![]() по частоте при одновременном изменении
его ширины в
по частоте при одновременном изменении
его ширины в![]() раз (при
раз (при![]() )
необходимо сформировать сигнал
)
необходимо сформировать сигнал![]() .
.
Спектр этого сигнала имеет вид:
![]() .
.
Если
изменение длительности сигнала
![]() в
в![]() раз
начать с момента времени
раз
начать с момента времени![]() ,
т.е. сформировать сигнал
,
т.е. сформировать сигнал![]() ,
то спектр этого сигнала будет иметь
вид:
,
то спектр этого сигнала будет иметь
вид:
![]() .
.
В
этом случае спектр сформированного
сигнала отличается от спектра
![]() исходного сигнала
исходного сигнала![]() по модулю, по ширине и по наличию у каждой
спектральной составляющей начального
фазового сдвига, равного
по модулю, по ширине и по наличию у каждой
спектральной составляющей начального
фазового сдвига, равного![]() .
.
При
цифровой обработке сигналов (ЦОС)
приходится иметь дело с преобразованием
Фурье сигнала, дискретизованного по
времени. Хотя многие из теорем и свойств
Фурье–анализа сигналов непрерывного
времени верны и в случае дискретно-временного
Фурье–анализа, прерывистость поступления
анализируемых отсчетов
![]() ,
где
,
где![]() указывает на номер отсчета в
последовательности, приводит все-таки
к изменению формы утверждений одних
теорем и к неприменимости других.
указывает на номер отсчета в
последовательности, приводит все-таки
к изменению формы утверждений одних
теорем и к неприменимости других.
Показательна в этом отношении пара преобразований Фурье: периодическая импульсная последовательность во временнoй области и ее преобразование Фурье, которое, как оказывается тоже является периодической импульсной последовательностью, но уже в частотной области.
Пусть
имеется бесконечная периодическая
последовательность единичных импульсов
![]() (не путать с единичной функцией),
показанная на рис. 7.7,а.
(не путать с единичной функцией),
показанная на рис. 7.7,а.

Рис. 7.7. Последовательность d-импульсов а) во временной области и ее спектр б)
Аналитическая форма представления последовательности d-импульсов во временной области:
![]()
иногда называется дискретизирующей последовательностью.
Каждый импульс в этой последовательности характеризуется следующими свойствами.
1.
Единичный импульс
![]() – дельта функция Дирака – это предел,
к которому стремится амплитуда импульса
длительностьюt,
имеющего единичную площадь, при стремлении
длительности к нулю t®0,
т.е.
– дельта функция Дирака – это предел,
к которому стремится амплитуда импульса
длительностьюt,
имеющего единичную площадь, при стремлении
длительности к нулю t®0,
т.е.
![]()
при
![]() .
.
2.
При сдвиге единичного импульса по оси
![]() на величину
на величину![]() условия (3.41) и (3.42) записываются в более
общей форме:
условия (3.41) и (3.42) записываются в более
общей форме:
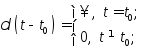

при
любом![]() .
.
Здесь
учтено, что
![]() –
функция, которая равна нулю всюду, за
исключением особой точки
–
функция, которая равна нулю всюду, за
исключением особой точки![]() ,
где она обращается в бесконечность, и
притом так, что интеграл от нее,
распространенный на сколь угодно малый
отрезок, заключающий особую точку, равен
единице. Последнее означает, что и в
этом случае площадь под
,
где она обращается в бесконечность, и
притом так, что интеграл от нее,
распространенный на сколь угодно малый
отрезок, заключающий особую точку, равен
единице. Последнее означает, что и в
этом случае площадь под![]() -импульсом
равна единице.
-импульсом
равна единице.
Единичному импульсу приписывают свойство четности
![]()
и
симметрии относительно особой точки
![]()
 ,
,
![]() .
.
3.
Для любой функции![]() ,
ограниченной и непрерывной в точке
,
ограниченной и непрерывной в точке![]() ,
справедливы равенства
,
справедливы равенства

и
 .
.
Это
фильтрующее свойство
![]() -функции.
-функции.
Если
же в точке
![]() функция
функция![]() имеет разрыв 1-го рода, то
имеет разрыв 1-го рода, то ,
где в скобках записана сумма пределов
функции
,
где в скобках записана сумма пределов
функции![]() ,
определенных слева и справа от точки
,
определенных слева и справа от точки![]() .
.
4. Спектр d-импульса равномерный на всех частотах с интенсивностью, равной единице, что следует из определения преобразования Фурье и из фильтрующих свойств d-функции
![]()
при
![]() =0
=0![]() .
.
5.
Результатом умножения произвольной
функции
![]() на
на![]() является дельта-функция
является дельта-функция![]() ,
площадь которой равна значению функции
,
площадь которой равна значению функции![]() в точке
в точке![]() :
:
![]()
Запись
![]() ,
вообще говоря, некорректна, хотя находит
применение в литературе при определении
выборочных значений сигнала
,
вообще говоря, некорректна, хотя находит
применение в литературе при определении
выборочных значений сигнала![]() .
.
Фильтрующее
свойство дельта-функции позволяет
представить аналоговый сигнал
![]() в виде суммы бесконечного числа
примыкающих друг к другу дельта-импульсов,
площади которых равны значениям
аналогового сигнала в соответствующие
текущие моменты времени
в виде суммы бесконечного числа
примыкающих друг к другу дельта-импульсов,
площади которых равны значениям
аналогового сигнала в соответствующие
текущие моменты времени![]() ,
с помощью формулы
,
с помощью формулы
![]() ,
,
где подынтегральное выражение записано с учетом пункта 5 свойств.
Широкое
использование
![]() -функции
в приложениях объясняется, в частности,
тем, что входные воздействия любой
формы, которые практически равны нулю
(достаточно малы) за пределами некоторого
короткого временно́го интервала,
вызывают, как правило, практически
одинаковый выходной эффект, если их
площади (интегралы по времени) равны.
Это обстоятельство делает единичный
импульс своего рода стандартным
импульсом, которым при анализе воздействий
на электрические цепи можно заменить
любой короткий реальный импульс с
единичной площадью. Иначе говоря,
дельта-функция является математической
моделью короткого внешнего воздействия
с единичной площадью. Однако, хотя
-функции
в приложениях объясняется, в частности,
тем, что входные воздействия любой
формы, которые практически равны нулю
(достаточно малы) за пределами некоторого
короткого временно́го интервала,
вызывают, как правило, практически
одинаковый выходной эффект, если их
площади (интегралы по времени) равны.
Это обстоятельство делает единичный
импульс своего рода стандартным
импульсом, которым при анализе воздействий
на электрические цепи можно заменить
любой короткий реальный импульс с
единичной площадью. Иначе говоря,
дельта-функция является математической
моделью короткого внешнего воздействия
с единичной площадью. Однако, хотя![]() считается чисто математическим объектом,
данное выше определение единичного
импульса не может быть обосновано
математически. Попытки строгого
обоснования приводят к неоднозначности,
несовместимости и «парадоксальности»
поведения (в частности, к утверждению,
что энергия
считается чисто математическим объектом,
данное выше определение единичного
импульса не может быть обосновано
математически. Попытки строгого
обоснования приводят к неоднозначности,
несовместимости и «парадоксальности»
поведения (в частности, к утверждению,
что энергия![]() -импульса
бесконечно велика при исходном условии,
что его площадь равна единице). Поэтому
целесообразно, согласно отказаться от
попыток определения значений
-импульса
бесконечно велика при исходном условии,
что его площадь равна единице). Поэтому
целесообразно, согласно отказаться от
попыток определения значений![]() ,
а учитывать только результаты его
воздействия и свойства. Иначе говоря,
,
а учитывать только результаты его
воздействия и свойства. Иначе говоря,![]() относится
к функциям, о которых надо знать, что
они «делают», а не то, чем они «являются».
Такие функции называются обобщенными
функциями.
относится
к функциям, о которых надо знать, что
они «делают», а не то, чем они «являются».
Такие функции называются обобщенными
функциями.
При
рассмотрении цифровой обработки сигналов
вместо функции
![]() зачастую более удобно пользоваться
функцией единичного отсчета
зачастую более удобно пользоваться
функцией единичного отсчета![]() ,
которая определяется следующим образом:
,
которая определяется следующим образом:
![]()
где
![]() – целое число.
– целое число.
Задержанная
функция единичного отсчета![]() ,
определяется как
,
определяется как
![]()
Дельта-функцию
![]() можно разложить в ряд Фурье на интервале
можно разложить в ряд Фурье на интервале![]() ,
используя равенство:
,
используя равенство:
![]()
Этим
рядом пользуются при вычислении
интегралов, содержащих
![]() -функцию,
производя почленное интегрирование
подынтегральной функции.
-функцию,
производя почленное интегрирование
подынтегральной функции.
Например,
в результате вычисления интеграла
![]() ,
в котором функция
,
в котором функция![]() разложена в ряд Фурье, после подстановки
вместо
разложена в ряд Фурье, после подстановки
вместо![]() правой части выражения , получается
правой части выражения , получается
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() ,
,
причем
![]() .
.
В
приложениях применяется усеченная
последовательность единичных импульсов
(пачка), число
![]() которых ограничено (рис. 2.14).
которых ограничено (рис. 2.14).
Применим
преобразование Фурье к последовательности
единичных импульсов
![]() .
С этой целью выделим из бесконечного
числа импульсов функции
.
С этой целью выделим из бесконечного
числа импульсов функции![]() только
только![]() импульсов, расположенных симметрично
относительно начала координат, как
показано на рис. 7.8,а.
импульсов, расположенных симметрично
относительно начала координат, как
показано на рис. 7.8,а.

Рис. 7.8. Усеченная последовательность единичных импульсов
Преобразование
Фурье
![]() такой усеченной последовательности
такой усеченной последовательности![]() равно
равно

Как
видно, преобразование Фурье
![]() выражается суммой
выражается суммой![]() комплексных экспоненциальных функций.
Огибающую
комплексных экспоненциальных функций.
Огибающую![]() можно найти, представив сумму экспонент
в виде первых
можно найти, представив сумму экспонент
в виде первых![]() членов геометрической прогрессии со
знаменателем, равным
членов геометрической прогрессии со
знаменателем, равным![]() .
После выполнения преобразований
.
После выполнения преобразований
![]() ,
,
Огибающая
![]() изображена на рис. 7.8,б.
изображена на рис. 7.8,б.
Из
формулы (3.55) следует, что максимумы
лепестков огибающей спектра
![]() со значениями
со значениями![]() расположены на частотах, кратных
расположены на частотах, кратных![]() ,
а ее нулевые значения наблюдаются на
частотах, кратных частоте
,
а ее нулевые значения наблюдаются на
частотах, кратных частоте![]() .
.
Если
теперь увеличивать число импульсов
так, чтобы
![]() ,
а
,
а![]() ,
то согласно , максимумы лепестков
,
то согласно , максимумы лепестков![]() будут возрастать, а их ширина –
уменьшаться. В результате огибающие
спектральных составляющих приближаются
по форме к единичным импульсам. При этом
для любого из
будут возрастать, а их ширина –
уменьшаться. В результате огибающие
спектральных составляющих приближаются
по форме к единичным импульсам. При этом
для любого из![]() импульсов площадь
импульсов площадь![]() каждого из лепестков останется равной
каждого из лепестков останется равной
 .
.
Здесь
следует иметь в виду, что все частные
суммы при любых
![]() ,
равны нулю, а поэтому
,
равны нулю, а поэтому
 .
.
Таким образом, бесконечная (периодическая) последовательность дельта-импульсов во временно́й области в процессе преобразования Фурье переходит в периодическую последовательность дельтаобразных спектральных составляющих, как это показано на рис. 7.8, б, и символически выражается парой преобразований Фурье
 .
.
Единичный
импульс иногда записывают в виде так
называемой функции единичного отсчета,
определяемой для всех
![]() формулами и . Последовательность
единичных отсчетов
формулами и . Последовательность
единичных отсчетов![]() ,
где
,
где![]() ,
аналогична рассмотренной последовательности
единичных импульсов. В свою очередь,
последовательность единичных отсчетов
формально эквивалентна (хотя бы в части
следования во времени) последовательности
выборок реального сигнала. Значит,
следует ожидать, что при Фурье –
преобразованиях равномерно разнесенных
друг от друга выборок также будет
наблюдаться периодическая повторяемость
основного спектра, определяемого формой
импульсов в выборке и ее продолжительностью.
Поэтому нельзя исключить возможность
частичного наложения повторяющихся
спектров. Такие наложения исказят
характеристики сигнала, получаемые по
результатам анализа его в частотной
области, и снизят точность воспроизведения
сигнала по его спектру.
,
аналогична рассмотренной последовательности
единичных импульсов. В свою очередь,
последовательность единичных отсчетов
формально эквивалентна (хотя бы в части
следования во времени) последовательности
выборок реального сигнала. Значит,
следует ожидать, что при Фурье –
преобразованиях равномерно разнесенных
друг от друга выборок также будет
наблюдаться периодическая повторяемость
основного спектра, определяемого формой
импульсов в выборке и ее продолжительностью.
Поэтому нельзя исключить возможность
частичного наложения повторяющихся
спектров. Такие наложения исказят
характеристики сигнала, получаемые по
результатам анализа его в частотной
области, и снизят точность воспроизведения
сигнала по его спектру.
Обратим
внимание на следующую особенность
преобразования Фурье усеченной
периодической последовательности
![]() единичных
импульсов
единичных
импульсов![]() .
Как следует из , и видно на рис. 7.8,
б,
максимумы всех лепестков спектра
.
Как следует из , и видно на рис. 7.8,
б,
максимумы всех лепестков спектра
![]() одинаковы, равно как одинакова и их
форма. Это объясняется тем, что единичные
импульсы в рассматриваемой последовательности
не имеют длительности (по определению).
То, что сами лепестки имеют определенную
(не нулевую) ширину, является следствием
конечной длительности пачки единичных
импульсов усеченной последовательности.
одинаковы, равно как одинакова и их
форма. Это объясняется тем, что единичные
импульсы в рассматриваемой последовательности
не имеют длительности (по определению).
То, что сами лепестки имеют определенную
(не нулевую) ширину, является следствием
конечной длительности пачки единичных
импульсов усеченной последовательности.
Реальные импульсные последовательности наряду с тем, что они всегда ограничены по длительности, к тому же состоят из импульсов конечной длительности. Для оценки того, как повлияет конечность ширины элементарных импульсов в их усеченной последовательности на характеристики ее спектра, рассмотрим следующий пример, раскрывающий особенности дискретизации сигнала в аналогово-цифровых преобразователях.
Пусть
формирование выборок принимаемых
сигналов осуществляется с помощью
электронного ключа. Соответствующую
операцию удобно рассматривать как
умножение сигнала, принимаемого
приемником, на вспомогательную
периодическую последовательность
![]() достаточно коротких, но с неравной нулю
длительностью тактовых импульсов. После
дискретизации любого реального сигнала
естественным образом формируется
усеченная последовательность отсчетов
в виде импульсов с разными амплитудами,
величины которых зависят от значений
исходного сигнала в интервалы времени
взятия отсчетов.
достаточно коротких, но с неравной нулю
длительностью тактовых импульсов. После
дискретизации любого реального сигнала
естественным образом формируется
усеченная последовательность отсчетов
в виде импульсов с разными амплитудами,
величины которых зависят от значений
исходного сигнала в интервалы времени
взятия отсчетов.
Тактовые
импульсы обычно полагают прямоугольными
импульсами с одинаковой длительностью
![]() ,
малой по сравнению с шагом дискретизации
,
малой по сравнению с шагом дискретизации![]() .
В данном случае также присутствует
идеализация, так как сформировать
идеально прямоугольные импульсы
невозможно, но это все же гораздо меньшая
идеализация, чем при представлении
тактовых импульсов последовательностью
единичных импульсов.
.
В данном случае также присутствует
идеализация, так как сформировать
идеально прямоугольные импульсы
невозможно, но это все же гораздо меньшая
идеализация, чем при представлении
тактовых импульсов последовательностью
единичных импульсов.
Пусть
в результате дискретизации аналогового
сигнала
![]() получен дискретный сигнал
получен дискретный сигнал
![]() .
.
Сигналы![]() ,
,![]() и дискретизирующие последовательности
и дискретизирующие последовательности![]() и
и![]() изображены на рис. 7.9.
изображены на рис. 7.9.

Рис.
7.9. Сигналы
![]() ,
,![]() и дискретизирующие последовательности
и дискретизирующие последовательности![]() и
и![]()
Если
известен вид спектральной плотности
![]() исходного аналогового сигнала
исходного аналогового сигнала![]() ,
можно найти спектр дискретизированного
сигнала
,
можно найти спектр дискретизированного
сигнала![]() .
Дискретизирующая последовательность
.
Дискретизирующая последовательность![]() ,
представляющая собой периодическую
последовательность прямоугольных
однополярных импульсов, записывается
с использованием ряда Фурье в виде:
,
представляющая собой периодическую
последовательность прямоугольных
однополярных импульсов, записывается
с использованием ряда Фурье в виде:
 ,
,
где
![]() – амплитуда тактового импульса;
– амплитуда тактового импульса;![]() – угловая частота следования тактовых
импульсов.
– угловая частота следования тактовых
импульсов.
Представив
![]() и введя обозначение
и введя обозначение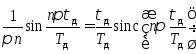 ,
можно получить
,
можно получить
 .
.
С учетом этого выражения примет вид
 .
.
Спектр
сигнала
![]() можно оценить непосредственно из без
выполнения каких-либо преобразований.
Ясно, что первому слагаемому в скобках
правой части соответствует спектральная
плотность
можно оценить непосредственно из без
выполнения каких-либо преобразований.
Ясно, что первому слагаемому в скобках
правой части соответствует спектральная
плотность![]() исходного аналогового сигнала
исходного аналогового сигнала![]() .
Далее, каждому из слагаемых произведений
.
Далее, каждому из слагаемых произведений![]() ,
согласно теореме о смещении спектра,
соответствует спектральная плотность,
определяемая соотношением
,
согласно теореме о смещении спектра,
соответствует спектральная плотность,
определяемая соотношением![]() .
С учетом сказанного, искомая спектральная
плотность равна
.
С учетом сказанного, искомая спектральная
плотность равна
 .
.
Поскольку
![]() ,
,![]() можно внести под знак суммирования и
окончательно записать
можно внести под знак суммирования и
окончательно записать
 .
.
Из
следует, что спектр
![]() дискретизированного сигнала включает
в себя последовательность смещенных
один относительно другого на
дискретизированного сигнала включает
в себя последовательность смещенных
один относительно другого на![]() спектров
спектров![]() исходного сигнала
исходного сигнала![]() таких, что их интенсивность убывает по
закону
таких, что их интенсивность убывает по
закону .
.
Если
шаг
![]() выбран таким, что
выбран таким, что![]() ,
где
,
где![]() - наивысшая верхняя частота в спектре
исходного сигнала
- наивысшая верхняя частота в спектре
исходного сигнала![]() ,
то смещенные спектры
,
то смещенные спектры![]() ,
,![]() ,
не будут перекрываться и, следовательно,
могут быть разделены фильтрами,
настроенными на соответствующие частоты.
Для того чтобы упростить создание таких
фильтров, а также при необходимости
обеспечения высокой точности
воспроизведения сигнала по имеющимся
выборкам, величину
,
не будут перекрываться и, следовательно,
могут быть разделены фильтрами,
настроенными на соответствующие частоты.
Для того чтобы упростить создание таких
фильтров, а также при необходимости
обеспечения высокой точности
воспроизведения сигнала по имеющимся
выборкам, величину![]() надо брать существенно меньшей, чем
надо брать существенно меньшей, чем![]() .
.
Выражение
указывает на то, что с уменьшением
![]() лепестки спектра убывают медленнее. В
пределе, при
лепестки спектра убывают медленнее. В
пределе, при![]() ,
спектр приобретает строго периодическую
структуру (уровень у всех лепестков
становится одинаковым, но стремится к
нулю). Но если одновременно с уменьшением
,
спектр приобретает строго периодическую
структуру (уровень у всех лепестков
становится одинаковым, но стремится к
нулю). Но если одновременно с уменьшением![]() увеличивать
увеличивать![]() ,
добиваясь
,
добиваясь![]() ,
то последовательность
,
то последовательность![]() перейдет
перейдет![]() ,
а
,
а![]() - в последовательность единичных
импульсов со взвешенными площадями (с
весами, равными
- в последовательность единичных
импульсов со взвешенными площадями (с
весами, равными![]() ),
т.е. при
),
т.е. при![]() можно записать:
можно записать:
![]() ,
,
а
![]() .
.
Соответствующие последовательности изображены на рис. 7.9.
Спектр дискретизированного сигнала в таком случае принимает вид
![]() ,
,
т.е.
продолжает оставаться непрерывным в
полосах шириной
![]() около каждой спектральной составляющей
частоты
около каждой спектральной составляющей
частоты![]() .
.
Представление
дискретизированного сигнала в виде
позволяет выразить спектральную
плотность
![]() через совокупность временны́х отсчетов
через совокупность временны́х отсчетов![]() без обращения к спектру
без обращения к спектру![]() исходного сигнала, применив к
преобразование Фурье при
исходного сигнала, применив к
преобразование Фурье при![]() :
:
![]() .
.
Такая возможность существенно упрощает спектральный анализ дискретных сигналов.
Спектр дискретизированного сигнала отличается от спектра непрерывного сигнала тем, что он периодичен по частоте. При цифровой обработке сигналов это создает проблему наложения спектров. Игнорирование эффекта наложения спектров может стать причиной появления существенных ошибок в процессе такой обработки.
