8. Представление сигналов рядом Котельникова

Для теории и практики цифровой обработки в различных радиоэлектронных системах широко используется представление сигналов рядом В.А.Котельникова

,

где n – целое число; s(nT_д) – значение исходного сигнала s(t), взятое в момент времени t=nT_д; – фиксированный интервал времени, разделяющий соседние точки отсчета на временной оси, т.е. период (шаг) дискретизации сигнала, аw_в – наивысшая учитываемая частота в спектре сигнала s(t).

Ряд в сходится к сигналу s(t), если коэффициенты разложения сигнала в ряд Фурье равны нулю при всех гармониках на частотах и не имеет особенности при. В этом случае отсчетыs(t), взятые в моменты , т.е. отсчетыs(nT_д), отстоящие друг от друга по времени на шаг T_д, полностью определяют s(t) и во все остальные моменты времени.

Ряд сходится, очевидно, и для любых интервалов взятия отсчетов , т.е. приw₁>w_в, так как спектр сигнала s(t), ограниченный интервалом (-w_в,w_в), тем более будет ограничен большим интервалом (-w₁,w₁). Отсюда следует, что шаг дискретизации является наибольшим интервалом между отсчетами, при котором ряд Котельникова точно аппроксимирует исходный сигнал. Иначе говоря, по отсчетам, взятым с интерваломT_д2>T_д, исходный сигнал с использованием ряда может быть восстановлен только с ошибками, а по отсчетам, взятым с интервалом T_д1£T_д, он будет восстановлен безошибочно. В общем случае, формула ряда Котельникова позволяет находить значение сигнала в любой момент времени, если известны его дискретные значения s(nT_д), путем решения интерполяционной задачи (рис. 8.1, б, в) с использованием, в качестве интерполяционных, функций .

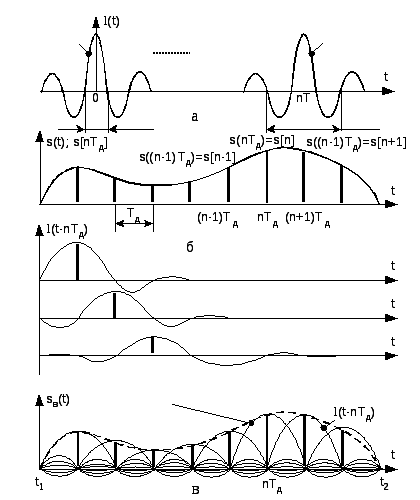
Рис. 8.1. Импульс, используемый при аппроксимации временной функции рядом Котельникова (а); отдельные слагаемые этого ряда, представленные импульсами вида (а) с амплитудами, равными (б) и восстановленный с использованием ряда Котельникова сигнал (в).

Выражение фактически описывает не что иное, как разложение аналогового сигнала в ряд по ортогональной системе функций вида:

,

называемой функцией отсчетов.

График этой функции изображен на рис. 2.16 а при n=0 и произвольном значении n.

Именно такую форму имеет напряжение отклика на выходе идеального низкочастотного фильтра, пропускающего все частоты от нулевой до граничной частоты w_в, когда на вход фильтра подается очень короткий импульс (в идеале – d-импульс). Основная часть одиночного импульса функции отсчетов приходится на интервал времени порядка , – в таком интервале содержится 78% энергии импульса. Этот интервал заключен между моментами времени, в которых значение импульса равно. Данный факт указывает на то, что в тех случаях, когда значения отсчетовs(nT_д) отличны от нуля только при , гдеn₁ и n₂ – натуральные числа, энергия сигнала в основном выделяется на временном интервале длины . Иначе говоря, можно считать, что данный сигнал реально существует только в пределах такого интервала.

Функция отсчетов имеет следующие свойства.

1. В момент времени t=nT_д она достигает своего максимального значения, равного 1.

3. В моменты времени t=(n±k)T_д, где k – любое целое число, она обращается в нуль, т.е. выполняется равенство

3. Функции отсчетов ортогональны на бесконечном большом времени .

4. Спектральная плотность функции равномерна в полосе частот и равнав ее пределах рис. 8.2, б и рис. 8.2, в.

Рис. 8.2. Спектральные плотности видеосигнала (а), импульса отсчетной функции (б), радиосигнала (в) и порядок следования частотных выборок (г).

Функции отсчетов sinc(0) и sinc(t-nT_д) отличаются друг от друга только сдвигом на оси времени, равным nT_д. Поэтому спектральная плотность импульса sinc(t-nT_д), в соответствии со свойством преобразования Фурье для сдвига сигналов во времени, составляет

и отличается от L(0) только фазовыми сдвигами соответствующих спектральных составляющих, равными wnT_д.

Разложение для строго ограниченной по полосе частот функции времени рис. 8.2, а (функции с финитным спектром) обобщается на случай произвольной полосы частот шириной Гц, имеющей своим центром некоторую угловую частотуw₀, т.е. на случай радиосигналов, спектры которых сосредоточены около частоты w₀, так что так, как это показано на рис. 8.2,в. Сигнал s(t), удовлетворяющий указанному условию, представляется в виде [ ]:

где s_s(t) и s_c(t) – временные функции (огибающие) со спектрами, отличными от нуля только на частотах .

Соотношение имеет не только теоретическое значение. Таким выражением описывается, например, сигнал, получаемый при модуляции с подавлением несущей, когда две квадратурные составляющие на несущей частоте sinw₀t и cosw₀t модулируются сигналами s_s(t) и s_c(t) соответственно. Таким же выражением может быть представлен сигнал после его разложения на квадратурные составляющие, что часто применяется в приемниках многих РЭС, в том числе в устройствах запоминания и воспроизведения сигналов с квадратурной обработкой.

Составляющие сигнала s_s(t) и s_c(t) разложимы в ряды . Поэтому можно записать

.

Здесь s_s[nT_д0] и s_c[nT_д0] равны значениям, которые принимают составляющие сигнала (3.67) s_s(t) и s_c(t) при . Эти значения образуют два отсчета, приходящиеся на единицу ширины полосы (в Герцах) и на единицу времени (в секундах).

Если известны спектры сигналов s_s(t) и s_c(t), то спектр сигнала s(t) может быть получен с учетом свойства смещения спектра сигнала при преобразованиях Фурье и свойства преобразования Фурье суммы сигналов. Пусть указанные выше сигналы имеют спектры S_s(w) и S_c(w). В этом случае спектр сигнала s(t) запишется в виде

Следовательно, если спектры S_s(w) и S_c(w) отличны от нуля лишь на частотах , то спектрS(w) будет отличен от нуля только на частотах .

Таким образом, в рассматриваемом случае точки взятия отсчетов отстоят друг от друга вдвое дальше, чем тогда, когда сигнал имеет спектр, начинающийся от нуля. Однако, теперь в каждой выборке должны быть определены значения двух сигналов s_s(t) и s_c(t). Следовательно, и здесь сигнал длительности T со спектром шириной f_в определяется тем же минимальным числом 2T×f_в независимых отсчетных значений.

Это, собственно говоря, проявление общей закономерности, связанной с тем, что при разложении функции в ряд Фурье число степеней свободы ее определяется числом соответствующих гармоник, но не тем, какой конкретно области частот лежат эти гармоники. В частности, линейное смещение спектра на оси частот не изменяет числа степеней свободы сигнала.

Если в спектре сигнала отсутствуют составляющие на частотах f<f_мин, то можно, воспользовавшись гетеродином, линейно сместить весь спектр на f_мин влево, т.е. до нуля. После такого смещения спектр будет занимать полосу частот от 0 до f_в=f_макс-f_мин и для смещенного сигнала будут выполняться условия представления рядом Котельникова. Число независимых отсчетов (степеней свободы) будет равно 2(f_макс-f_мин)T, где T – длительность сигнала. Таким образом, при ограничении спектра снизу отсчеты можно брать реже, чем это задается частотой f_макс. Этот прием применяется в современных ЦУЗВС.

Представление сигнала рядом Котельникова предполагает использование бесконечного числа выборочных значений – отсчетов из бесконечно длящегося сигнала. Однако, реальные сигналы всегда конечны, их длительность ограничена некоторым промежутком времени, например, от t₁ до t₂, равным t₂-t₁=T. Поэтому на практике достаточно ограничиться рассмотрением ряда

где – полное число отсчетов, которое должно быть снято с сигналаs(t) за время его длительности, для представления s(t) рядом Котельникова с приемлемой точностью. Дело в том, что разложение сигнала s(t) на конечном интервале времени T в принципе не может быть точным, так как фактически означает попытку применения преобразования Фурье, верного для сигналов с ограниченным спектром, к сигналу, который таковым не может быть по определению. Как следствие, сигнал с ограниченным спектром, наблюдаемый в течение ограниченного интервала времени T, может быть восстановлен по N=2f_вT отсчетам лишь приближенно. Непосредственно из и рис. 8.2 в видно, что погрешность равна нулю в точках отсчета, отлична от нуля между отсчетами, причем растет с приближением к краям интервала T, т.е. к точкам оси времени t₁ и t_3. Увеличение числа отсчетов снижает максимальную погрешность.

Спектральная плотность сигнала также может быть представлена рядом Котельникова, т.е. в виде последовательности частотных выборок. В качестве аппроксимирующей функции в этом случае используется функция вида

,

где – разнос по частоте между соседними частотными выборками;T – полная длительность сигнала.

Спектральная плотность S(w) аппроксимируется рядом

,

где – наивысшая частота в спектреS(w), а 2f_вT – число степеней свободы сигнала s(t), имеющего спектр S(w) или, иначе, общее число независимых отсчетов значений параметров, т.е. минимальное их число, которое необходимо для полного задания сигнала. Порядок следования выборок в частотной области показан на рис. 8.2 г.

Как видно, частотный интервал между выборками не должен превышать , иначеS(w) по имеющимся выборкам будет восстанавливаться с ошибками. При ширине спектра 2w_в, перекрывающей полосу частот -w_в<w<w_в, минимальное число выборок равно , т.е. как и в случае .

В общем случае выборочные значения спектра сигнала представляются комплексными числами. Это означает, что в каждой отсчетной точке, взятой на оси частот, должны задаваться (измеряться) два параметра в виде действительной и мнимой частей или в виде модуля и аргумента. При таком задании общее число параметров получается вдвое бoльшим, чем при представлении рядом , если число выборок в обоих случаях одинаково. Избыточность представления сигнала в частотной области устраняется тем, что учитывается комплексная сопряженность отсчетови, при которой спектр сигнала полностью характеризуется совокупностью комплексных выборок, взятых только в области положительных частот. Ведь задание одной из комплексно – сопряженных величин однозначно определяет другую. Главное, что при учете выборок, взятых только в области положительных частот, число независимых параметров (степеней свободы) остается минимально необходимым для безошибочного восстановления сигнала, поскольку равноN=2f_вT.

Заметим, что хотя здесь ряд Котельникова выделен особо, на самом деле он также относится к классу обобщенных рядов Фурье. Правда, уравнение , будучи справедливым, как и другие виды рядов, для комплексных и действительных функций, легко может быть распространено на функции времени, не имеющие Фурье-преобразования, такие, например, как стационарные шумовые сигналы, удовлетворяющие условию

,

где N(w) – спектральная плотность мощности стационарного шума.

Справедливы следующие замечания, касающиеся представления сигналов рядом Котельникова:

1. Условия применимости ряда Котельникова не накладывают никаких ограничений на конкретный вид спектра внутри интервала частот (0, w_в) или, в общем случае (w₁, w₂).

3. Поскольку функция отсчетов sinc(t-nT_д) затухает быстро, влияние каждого отсчета в уравнении ограничено небольшим временным интервалом. Поэтому сигнал, существующий только на временнoм интервале (t₁, t₂), даже если он не стремится к нулю в граничных точках t₁, t₂, с большой степенью точности определяется его значениями (отсчетами) в N=2Tf_в точках внутри интервала (t₁, t₂) протяженностью Т=t₂ -t₁. Наибольшие ошибки имеют место при определении сигнала непосредственно в окрестностях точек t₁ и t_3.

4. Невозможно существование функции, описывающей сигнал, ограниченный во времени и одновременно имеющий ограниченный частотный спектр. Однако всегда можно подобрать для описания сигнала функцию, соответствующую энергии сигнала, которая почти вся сосредоточена в конечных интервалах времени и полосы частот. Это означает, что всегда сигнал длительности, спектр которого практически ограничен полосой частот ширинойf_в, с высокой точностью определяется его значениями в 2Tf_в точках отсчета, разнесенных друг от друга по времени на . Такое число отсчетных точек требуется, если выборки берутся в центрах (средних точках) интервалов отсчетов. Если же отсчеты берутся на краях указанных интервалов, то число точек отсчета должно быть равно (2Tf_в+1).

4. Спектр S(w) сигнала, тождественно равного нулю вне интервала, однозначно определяется рядом Котельникова в частотной области, записанным для последовательности значенийS(w), взятых в точках частотной оси, отстоящих на [рад/с] друг от друга.

Если же длительность сигнала лишь приблизительно равна , а спектр его приблизительно ограничен частотой, и при этом, то спектральная функция сигнала весьма точно определяется (Tf_в+1) ее значениями в точках отсчета, отстоящих на расстоянии Герц или, рад/с друг от друга. Требуются неTf_в, а Tf_в+1 выборочное значение, поскольку надо учесть значение сигнала на нулевой частоте.

Уменьшение минимально необходимого числа выборочных значений практически в два раза не означает, однако, соответствующего уменьшения числа отсчетов, представляющих спектр. Суть в том, что спектральная плотность описывается комплексной функцией. Поэтому каждая выборка на частотах, отличных от нулевой, дает значения ее вещественной и мнимой частей. В результате общее число независимых данных – отсчетов, задаваемых (Tf_в+1) выборками, для однозначного определения спектральной функции, будет равно . Таким образом, никакого выигрыша в числе отсчетных значений в данном случае не получается.

5. Неверно утверждение о том, что сигнал длительности , имеющий ограниченный спектр, полностью характеризуется 2f_вT отсчетами. Ими он может быть представлен только с конечной точностью, хотя, может быть, и высокой.