Контрольные вопросы к разделу 4

1. Какие сигналы называются непрерывными, а какие – дискретными?

2. Какие сигналы называются пространственно-временными?

3. С какими сигналами работают цифровые радиоэлектронные системы?

4. Перечислите основные диапазоны электромагнитных волн.

5. Где и по каким физическим причинам возникают радиопомехи?

6. Внутренние и внешние помехи. Опишите причины возникновения и особенности внутренних и внешних помех.

5. Аналитические модели сигналов

Самая простая и самая распространенная модель, используемая при исследовании и проектировании радиоэлектронных систем и устройств, это модель гармонического (синусоидального) сигнала

,

где а – амплитуда, – частота, а– начальная фаза сигнала, аt – время tÎ[0,¥).

Дискретный (импульсный) сигнал характеризуется формой импульсов, их длительностью и периодом повторения, обратным частоте их следования.

Среди электрических сигналов негармонической формы выделяются импульсные сигналы (рис. 2.1 б), которые получили наиболее широкое распространение в радиоэлектронных устройствах и системах.

Разумеется, гармонический сигнал вида имеет бесконечно большую энергию, что противоречит естественным физическим представлениям. Поэтому такая модель не всегда может рассматриваться как адекватная. Кроме того, от полностью известен и точно предсказуем для любого момента времени tÎ[0,¥). Он не содержит какой-либо неожиданности и, следовательно, не может переносить информацию. Для того, чтобы наделить сигнал возможностью переносить сообщения, его параметры изменяют в соответствии с этим сообщением C(t). Процесс воздействия передаваемого сообщения на параметры несущего колебания называют модуляцией. У колебания вида таких параметров три: амплитуда, частота и начальная фаза. Поэтому возможны три способа модуляции: амплитудная (АМ), частотная (ЧМ) и фазовая (ФМ). В процессе модуляции изменяется форма сигнала. Аналитическая модель модулированного сигнала

,

где Ф(t) – полная фаза сигнала

.

Амплитуда сигнала не может быть отрицательной, поэтому в

.

Для выполнения условия обычно считается, что передаваемое сообщение (модулирующая функция) принимает значения на интервале [-1;1], а коэффициент глубины амплитудной модуляции не превосходит единицы m_ам£1.

Осциллограмма синусоидального колебания, модулированного по амплитуде гармоническим сигналом, иллюстрируется рис. 4.1.

Рис. 5.1. Графическая модель АМ колебания

Как видно из , модуляция гармонического сигнала по частоте, когда w зависит передаваемого от сообщения и, следовательно, от времени, эквивалентна модуляции фазы этого колебания, но по закону интеграла от частоты. Соответственно модуляция фазы может рассматриваться как модуляция частоты, но по закону производной от сообщения. На основании этих рассуждений частотную и фазовую модуляции можно объединить и рассматривать с единых позиций как угловую модуляцию. Амплитуда сигнала с угловой модуляцией постоянна, как на рис. 5.2.

Рис.5.2. Синусоидальный сигнал, модулированный по частоте гармоническим колебанием

Амплитуда изменения частоты в процессе ЧМ называется девиацией частоты f_д. Отношение девиации частоты к частоте модулирующего колебания (при гармонической модулирующей функции) – это индекс ЧМ:

.

Большой отдельный класс моделей – аналитические модели импульсных сигналов. Импульсные сигналы описываются разрывными функциями. Многообразие форм импульсов бесконечно. Но чаще всего используют следующие основные модели разрывных функций и импульсных сигналов.

1. Функция знака s(t)=sign(t) (сигнум-функция). Функция равна константе всюду, кроме точки t=0. В точке t=0 сигнум-функция скачком изменяет знак с -1 на +1:

Рис. 5.3. Функция знака (сигнум-функция)

Умножение любой функции f(t) на sign(t) означает изменение знака f(t) в момент времени t=0.

2. Единичная функция (единичный скачок, функция Хивисайда) рис. 5.4. s(t) определяется как

Рис. 5.4. Единичный скачок (функция Хивисайда)

Очевидно, что

.

Умножение любого сигнала s(t) на s(t) равносильно включению этого сигнала в момент t=0:

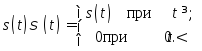
Такое представление широко используется для представления односторонних и вообще финитных (ограниченных во времени) сигналов.

3. Дельта-функция Дирака d(t). По определению d-функция удовлетворяет двум условиям:

и

.

Таким образом, d-функция представляет собой предел, к которому стремится импульс, имеющий любую форму и площадь, равную единице, при неограниченном укорочении длительности. Для того, чтобы подчеркнуть такую исчезающее малую протяженность d-функции по аргументу ее графически изображают отрезком вертикальной линии рис.5.5.

Рис. 5.5. d-функция Дирака

обладает целым рядом замечательных свойств, а именно:

3.1. d(t) является четной функцией своего аргумента

.

Из следует, что

.

Поэтому

Сопоставляя и можно установить, что

Иначе говоря, используя d-функцию можно выразить производную разрывной функции в точке разрыва.

3.2. Фильтрующее свойство d-функции

при , т. е. интеграл от произведенияd-функции и произвольной функции f(t), ограниченной на интервале (a,b), равен значению этой функции в точке t=t₀.

3.3. В результате умножения d-функции на произвольную функцию f(t) образуется d-функция, площадь которой равна значению f(t) в точке t=t₀:

.

3.4. Энергия d-импульса бесконечно велика. Это прямо следует из представления d-импульса как предела прямоугольного импульса длительностью t с амплитудой . Энергия такого импульса пропорциональна квадрату его амплитуды и первой степени длительности, т. е..

4. Прямоугольный импульс с единичной амплитудой и длительностью t рис. 5.6. аналитически представляется соотношением

Рис. 5.6. Прямоугольный импульс